どうも、木村(@kimu3_slime)です。
今回は、微積分学で扱う広義積分とは何か、なぜ学ぶか(ガウス積分とガンマ関数)について、簡単に紹介したいと思います。
広義積分とは何か
(広義ではない)普通の積分は、有限の大きさを持った閉区間\([a,b]\)が積分範囲となっていました。
例えば、\(f(x)=\frac{1}{\sqrt{x}}\)とすると、\(f\)は\(x\to 0\)で発散するので、\([0,1]\)では定義されていません。なので普通の意味では\([0,1]\)において積分不可能です。
広義積分では、このような関数の「積分」を考えることができます。まず、\(0<c<1\)として、閉区間\([c,1]\)で積分をすることはできますね。
\[ \begin{aligned}\int_c ^1 \frac{1}{\sqrt{x}}dx =[2 \sqrt{x}]^1_c =2-2\sqrt{c}\end{aligned} \]
ここで\(c\to0\)の極限を取ったときの、通常の積分の極限値を広義積分(improper integral)と定義するわけです。
\[ \begin{aligned}\int _0 ^1 \frac{1}{\sqrt{x}}dx := \lim _{c\searrow 0}\int_c ^1 \frac{1}{\sqrt{x}}dx =2 \end{aligned} \]
これは数列において、「無限和」なるものを有限和の極限として定義したのと同じ論法です。
\[ \begin{aligned}\sum_{n=1} ^\infty a_n := \lim_{k\to\infty} \sum_{n=1} ^k a_n \end{aligned} \]
無限区間における\([0,\infty)\)広義積分も、同様にして考えられます。
\[ \begin{aligned} \int _r ^{\infty} \frac{1}{x^2}dx &= \lim _{r_0 \to \infty } \int _r ^{r_0} \frac{1}{x^2}dx \\ &= \lim _{r_0 \to \infty } ([-\frac{1}{x}]_r ^{r_0}) \\ &= \lim _{r_0 \to \infty } (\frac{1}{r}-\frac{1}{r_0}) \\ &= \frac{1}{r}\end{aligned} \]
積分区間は無限に広いですが、その面積は有限値として確定しているのです。
物理学、力学において、\(f(x)=\frac{1}{x^2}\)(を定数倍したもの)は万有引力であり、その力の(位置に関する)積分は位置エネルギーと呼ばれる量です。万有引力の位置エネルギーを考えるときには、無限遠\(r_0=\infty\)を基準に取ることが多いです。つまり、\([r,\infty)\)における広義積分を考えていて、無限遠を基準にすることで式が単純になります。(電荷のエネルギー、クーロンの法則も同様の式です)
今回、広義積分が収束しているのはたまたまです。例えば\(\int_0 ^{1} \frac{1}{x} dx=\infty\)と発散する例はいくらでもあります。
広義積分の例:ガウス積分とガンマ関数
僕が始めて広義積分の話を知ったとき、それが計算できるのはわかるけれど、どんな応用があるのか知りませんでした。
広義積分の応用は幅広いですが、あえて2つ有名な例を挙げるとすれば、ガウス積分とガンマ関数になるでしょう。
ガウス積分は、次の広義積分です。
\[ \begin{aligned}\int_{-\infty} ^{\infty} e^{-x^2}= \sqrt{\pi} \end{aligned} \]
被積分関数\(e^{-x^2}\)(やその変形)は、ガウス関数、ガウス分布と呼ばれています。
ガウス積分やガウス分布は、統計学において重要な役割を果たしています。
表が確率\(p\)、裏が\(1-p\)で出るようなコインを、連続で投げる試行(ベルヌーイ)を考えると、\(n\)回投げたときに表が出る回数は、
\[ \begin{aligned}{{\displaystyle f(x) = {}_n C_x \, p^x (1-p)^{n-x} \quad (x\in \mathbb {N} )} }\end{aligned} \]
という二項分布(と呼ばれる確率密度関数)に従います。この\(x\)は離散的な値を取りますが、試行回数が大きくなると、それは次の正規分布
\[ \begin{aligned}{{\displaystyle f(x)={\frac {1}{\sqrt {2\pi \sigma^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma^{2}}}\right)\quad (x\in \mathbb {R} )} }\end{aligned} \]
に従うことが知られているのです(De Moivre–Laplace theorem)。二項分布は、試行回数が多ければ正規分布で近似できる。正規分布のなす釣り鐘状の曲線は、ベルカーブと呼ばれています。
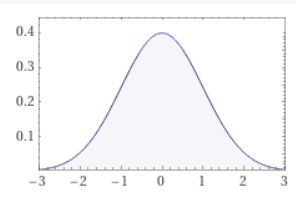
画像引用:Wolframalpha
正規分布の積分は
\[ \begin{aligned}\int _{-\infty }^{\infty} {\frac {1}{\sqrt {2\pi \sigma^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma^{2}}}\right) dx =1\end{aligned} \]
です(ガウス積分を変数変換すればわかる)。これは全ての事象が起こる確率の合計が1になることを意味します。そして、
\[ \begin{aligned}P(a<X \leq b)=\int _{a}^{b} {\frac {1}{\sqrt {2\pi \sigma^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma^{2}}}\right) dx \end{aligned} \]
は確率変数が\(a\)以上\(b\)以下の値を取る確率を表します。例えば平均から大きく外れた値を取る確率は少ないわけですが、それがどれくらい少ないかを表すための定式化として広義積分はあります。標準正規分布表という、積分を計算するための数表があるくらい、活用されているのです。
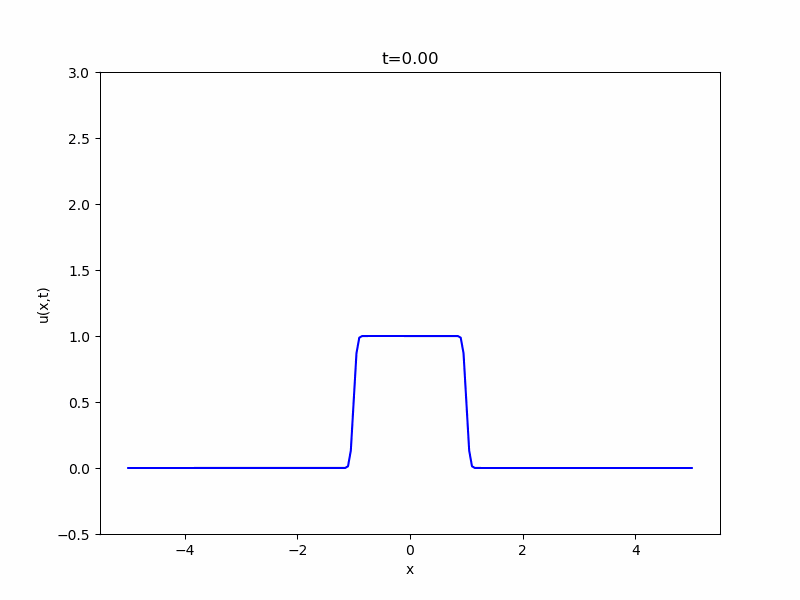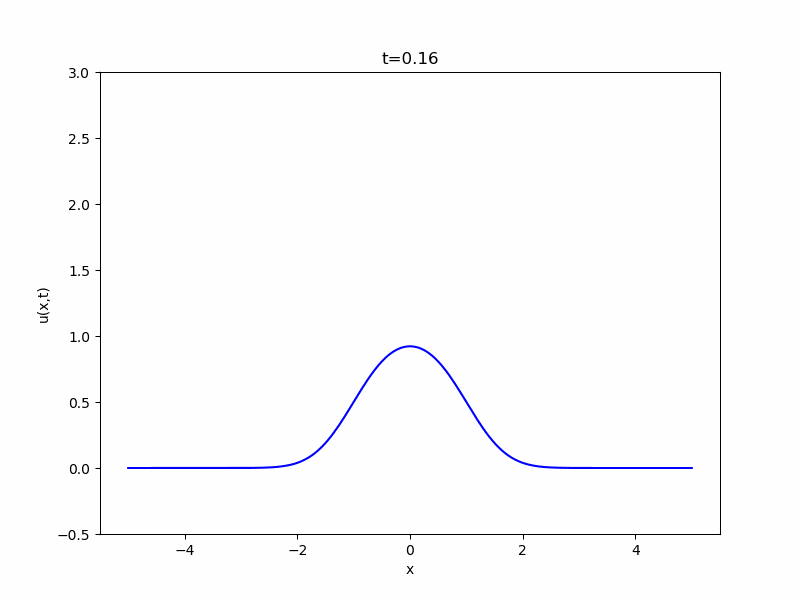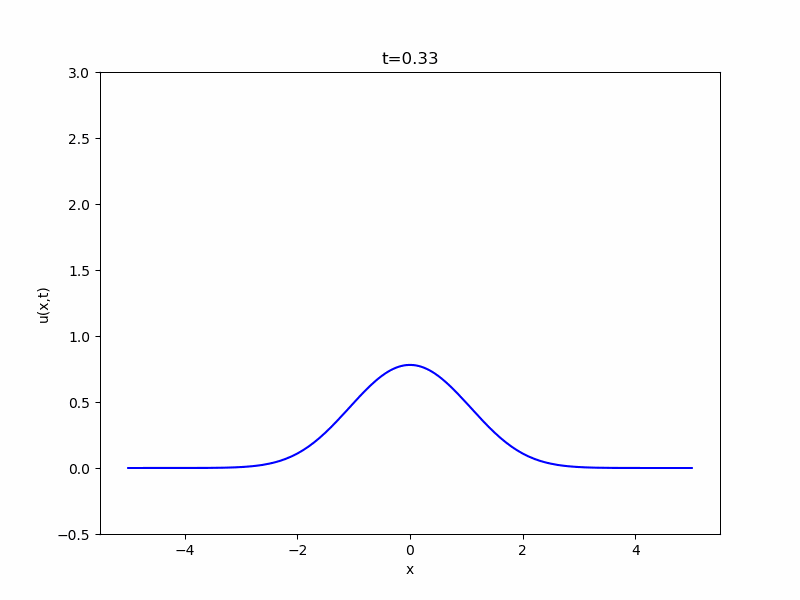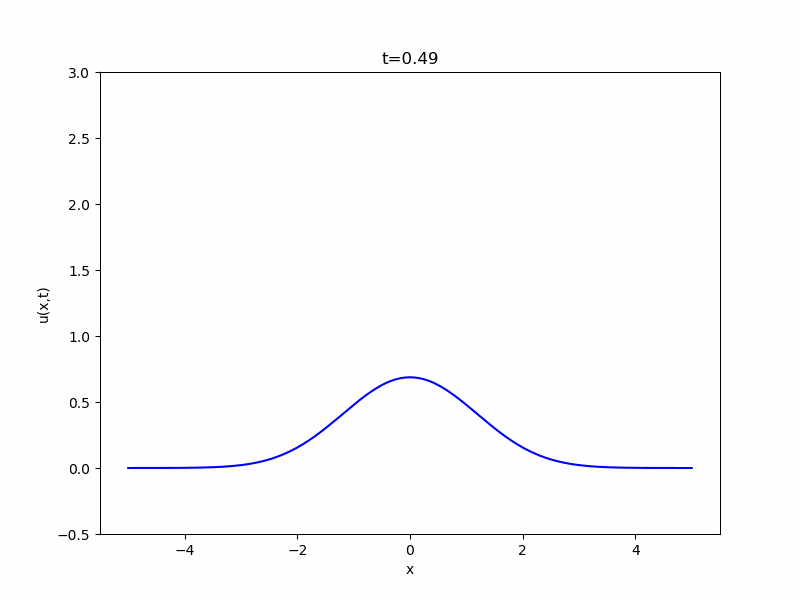
また、物理学において、広い空間における熱の拡散現象を考えると、基本解・熱核
\[ \begin{aligned}K(x,t)= \frac{1}{(4\pi t)^{\frac{N}{2}}} e^{-\frac{|x|^2}{4t}}\end{aligned} \]
と呼ばれる関数の積分が登場します。これもガウス関数の変形ですね。およそこのような関数に従って熱が拡散していくことが、次のアニメから感じ取れるでしょう。
ガウス積分と同様、有名な広義積分がガンマ関数です。
\[ \begin{aligned}\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}dt\end{aligned} \]
\(x=n\)(自然数)のとき、\(\Gamma (n)= (n-1)! \)と階乗関数に一致するという強い性質があります。さらには、\(x\)が自然数でなくても、負の数であっても、(複素数であっても)ガンマ関数は値を持つ(広義積分が収束する)のです。
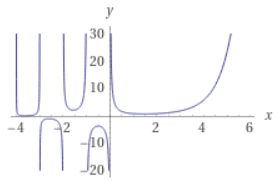
画像引用:Wolframalpha
その特殊値\(\Gamma (\frac{1}{2})\)は、変数変換によって\(\Gamma (\frac{1}{2})=\int_{-\infty} ^{\infty} e^{-x^2}= \sqrt{\pi}\)とガウス積分であることがわかります。ガンマ関数は、ガウス積分をも含む存在と言えるでしょう。
また、\(N\)次元の球\(B_N(a)=\{x \in \mathbb{R}^N \mid \|x\| \leq a\}\)の体積(重積分によって定義される)には、
\[ \begin{aligned}V_N(a) = \frac{\pi^{\frac{N}{2}} a^N}{\Gamma(\frac{N}{2}+1)}\end{aligned} \]
とガンマ関数が登場します。
以上、広義積分とは何か、それを学ぶ理由となる例として、ガウス積分とガンマ関数を紹介してきました。
その2つの例は多くの性質と応用を持つので、別記事でも紹介する予定です。
今回の話を通して、広義積分の定義だけではなく、それが広い応用・つながりを持った考え方であることを、感じ取ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080