どうも、木村(@kimu3_slime)です。
高校数学で三角関数を扱うときに、\(90^\circ\)のような度数法ではなく、ラジアン(弧度法)を使うようになります。
それはなぜなのか、三角関数の微分の単純化という視点から紹介します。
2種の三角関数を比較する
三角関数は、直角三角形の角度\(x\)に対して、その辺の長さの比を対応させる関数です。サイン=高さ/斜辺、コサイン=底辺/斜辺といった具合に。
三角関数の議論では、\(x\)としてラジアン(弧度法)を用います。\(180 ^\circ \)を\(\pi\)ラジアンと対応させるわけです。
このように\(x\)を定めるときの三角関数を、\(\sin x,\cos x,\tan x\)と表記します。例えば、\(\sin \pi = 0\)です。通常の三角関数をあえて、弧度三角関数と呼ぶことにしましょう。
一方で、度数法を使った三角関数も定義できます。例えば、\(180^{\circ}\)のサインは0、すなわち\(\sin ^{*} 180 =0\)といったように。一般には、\(\sin ^{*}x = \sin (\frac{\pi}{180}x)\)と定めれば、度数法と弧度法が対応します。このようにして定義した\(\sin ^{*} x, \cos ^{*}x, \tan ^{*}x\)を、度数三角関数と呼びます。
三角関数の基本的な性質(周期性や加法定理)は、弧度だろうが度数だろうが同様に成り立っています。
では、なぜ弧度三角関数が優先して教えられているのでしょうか? その理由のひとつは、微分の計算が単純になるからだと僕は考えています。
弧度三角関数については、
\[ \begin{aligned}\frac{d}{dx}(\sin x) = \cos x ,\frac{d}{dx}(\cos x) = -\sin x\end{aligned} \]
という性質が成り立ちます。一方で度数三角関数の微分を計算すると、
\[ \begin{aligned}\frac{d}{dx}(\sin^{*} x) = \frac{\pi}{180}\cos^{*} x ,\frac{d}{dx}(\cos^{*} x) = – \frac{\pi}{180}\sin^{*} x\end{aligned} \]
と、係数\(\frac{\pi}{180}\)が出てきてしまいます。
三角関数は多項式で近似できますが(テイラー展開)、それには三角関数を何度か微分したときの値が係数として登場し、
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots\end{aligned} \]
\[ \begin{aligned}\sin^{*} x= \frac{\pi}{180} x- (\frac{\pi}{180})^3 \frac{x^3}{3!}+ (\frac{\pi}{180})^5\frac{x^5}{5!}- \cdots\end{aligned} \]
となります。こうして見れば、弧度三角関数\(\sin x\)と度数三角関数\(\sin^{*}x \)、どちらを採用したいかは明白ですね。
どちらを採用しても本質的に同じですが、それならば計算が単純になるように定義しておきたいものです。だから、ラジアン(弧度法)を学び、度数法を(あまり)使わなくなっていくのですね。
つまり、微積分を学ばないうちは、弧度法のメリットや三角関数を学ぶ意義を感じにくいのではないかと思います。
参考:サイン、コサインは何の役に立つ? バネの振動と三角関数
(上に示した級数展開を、逆に三角関数の定義として採用することもできます。また、2回微分がそのマイナスに等しい\(f^{\prime\prime} (x)= -f(x)\)という微分方程式の解としても、三角関数は定義できます。)
弧度法が微分を単純化するのはなぜか
弧度法は、三角関数の微分が単純となるような表記法です。
\[ \begin{aligned}\frac{d}{dx}(\sin x) = 1\cdot \cos x\end{aligned} \]
微分の定義に戻って考えると、これは
\[ \begin{aligned}\lim_{h\to 0} \frac{\sin h}{h} = 1\end{aligned} \]
となる事実に支えられています。度数法では、\[ \begin{aligned}\lim_{h\to 0} \frac{\sin^{*} h}{h} = \frac{\pi}{180}\end{aligned} \]となってしまうわけです。
この極限が単純になるのは、次のような面積評価によって示されます。
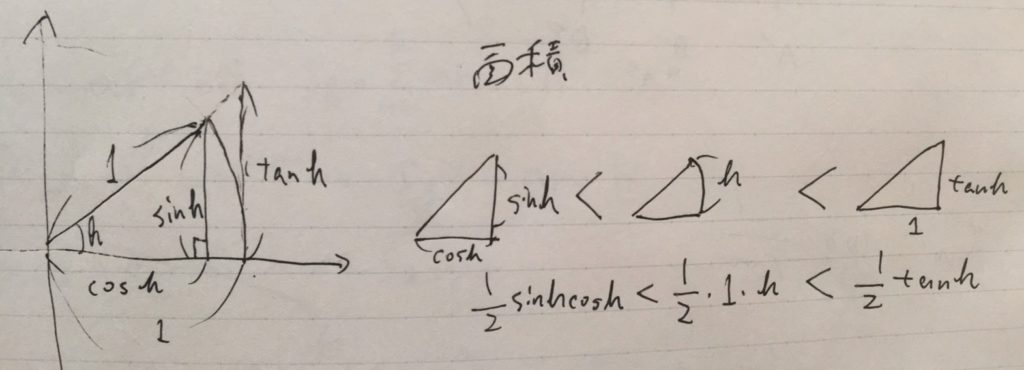
扇形の図形の面積\(S\)は、円の半径\(r\)と円弧の長さ\(\ell\)をかけて2で割ったものです\(S= \frac{1}{2} r \ell\)。ここで、円弧の長さは、弧度法を使えばちょうど角度に等しいです\(\ell =h\)。度数法では、\(\ell = \frac{\pi}{180}h\)となります。これが根本的な違い。
面積を評価した不等式を整理すれば、\(\cos h < \frac{h}{\sin h} < \frac{1}{\cos h}\)で、はさみうちの原理により\(\lim_{h\to 0} \frac{\sin h}{h} = 1\)が得られます。
まとめると、極限値を求めるために、三角形と円弧の面積を比較しています。円弧の面積は、円弧の長さに比例する。そのときに、「円弧=角度の\(\frac{\pi}{180}\)倍」とする角度の測り方(度数法)ではなく、「円弧=角度の\(1\)倍」となる角度の測り方(弧度法)を用いれば、\(\sin h \simeq h\)ときれいな式で近似できるわけです。
(細かいことを言えば、円や扇形の図形の面積は積分で定義され、それ求めるのに三角関数の微分を用いるから循環論法ではないか、というような話があります。しかし実際は、循環論法にはならずに示せることです。参考:sinx/xの極限は?x→0とx→∞の場合を証明付きで東大医学部生が教えます!、「高校数学における三角函数の微積分は循環論法になっている」というデマについて )
以上、ラジアン(弧度法)を学ぶ理由として、弧度三角関数と度数三角関数を比較し、弧度法では微分が単純となることを説明してきました。
指数関数や対数関数の定義で、\(e\)(オイラー数)を学ぶのも、微分が単純になるからです。これは別記事で紹介予定。
数学では、計算が簡単になるように定義を調整することがあります(正規化)。ラジアンを学び始めてその意義を疑問に思ったら、微分が単純に表せるという関係式まで学んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170