どうも、木村(@kimu3_slime)です。
データサイエンスという言葉を聞いたことがあるけど、どんなものか勉強したことがない。
今回は、そんな方に読み放題サービスKindle Unlimitedの対象となっている「大学4年間のデータサイエンスが10時間でざっと学べる」を紹介します。
どんな本か
「大学4年間のデータサイエンスが10時間でざっと学べる」は、データサイエンスに関する話題の全体像が短くまとめられたです。数式が登場する箇所は少なく、登場したとしても補足説明が多いです。
データサイエンティストとは何かというと、本書では
コンピューティング技術を活用し、データの収集と処理、統計学や機械学習的分析、意思決定や商品開発までの一連の流れを効果的に処理する技能をもつ人
引用:大学4年間のデータサイエンスが10時間でざっと学べる p.18
とされています。アカデミックの研究者というよりは、実学的で、企業・ビジネス的な面が大きいわけですね。
僕はこの本を、データサイエンスにおいて数学がどう応用されているか、理論に関してどんな数学的知識が求められているかを知るために手に取りました。
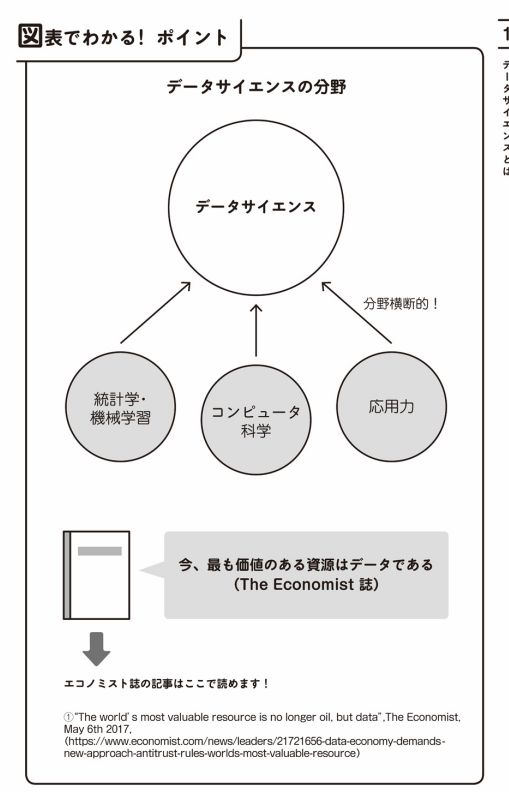
引用:大学4年間のデータサイエンスが10時間でざっと学べる p.19
この本は、1ページ文章1ページ図とかなり多く図解してくるので、流し読みに良いですね。統計学・機械学習が挙げられているのはよく見かけますが、コンピュータサイエンスまで含まれているのは特徴的だと思いました。
例えば計算量の理論では、微積分学で登場するO-記法(ランダウの記号)が登場しています。最適化問題にも微積分学の知識が必要ですね。
参考:関数のオーダー評価(ランダウの記号)をわかりやすく解説
ネットワーク分析では、グラフ理論、グラフが登場する。これは数学でいえばトポロジーとも関係する分野です。
統計学、微積分学、線形代数が全体として必要とされることを除けば、計算量の理論、最適化問題、機械学習、ディープラーニングに関して、数学の本ではなくその分野の専門書を読む必要があると感じました。
目次
- 第1部 データサイエンスの基本
- 01 データサイエンスとは
- 第2部 データサイエンスの基礎技術
- 02 計算機の仕組み
- 03 プログラミングの基礎(1)
- 04 プログラミングの基礎(2)
- 05 アルゴリズム(1)
- 06 アルゴリズム(2)
- 07 データベース
- 08 最適化の方法
- 第3部 統計学・機械学習の基礎
- 09 機械学習の基本
- 10 過学習とモデル選択
- 11 回帰問題と住宅価格
- 12 アンサンブル学習と住宅価格
- 13 分類問題
- 14 教師なし学習
- 第4部 コーパスとネットワークの分析
- 15 トピックモデル
- 16 ネットワーク分析
- 第5部 ディープラーニング
- 17 ニューラルネットワークの基礎
- 18 ディープラーニング
- 19 ディープラーニングによる系列データ分析
- 20 ディープラーニングによる画像分析
気になる点
この本は、あくまで要点が知れる本で、1から教科書のように学べる本ではないです。説明が不足していて、よくわからないと感じる部分もあります。短くわかる分、詳しくは理解できないので、興味を持った話題は自分で調べる必要があるでしょう。
また、可変レイアウトではなく固定レイアウトなので、PCやタブレットで読む分には問題ないですが、スマホからだと文字が小さく感じるでしょう。
「大学4年間のデータサイエンスが10時間でざっと学べる」はKindleの読み放題サービスKindle Unlimitedに登録してあれば無料なので、ぜひ試しに読んでみてください。数学・理論を駆使するというよりは、そこに至るまでのコンピュータサイエンス・データサイエンスの発展が感じられて面白いです。
木村すらいむ(@kimu3_slime)でした。ではでは。
KADOKAWA (2018-03-24T00:00:00.000Z)
¥1,485
こちらもおすすめ
コンピュータによる計算(アルゴリズム)とは何か、モデル化の方法、その限界は?
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方


