どうも、木村(@kimu3_slime)です。
トポロジーという言葉を聞いたことがあるでしょうか。位相幾何学とも呼ばれる大学数学の幾何学の分野のひとつで、ゴムのように柔らかくい「形」を扱います。
今回は、読み放題サービスKindle Unlimitedの対象となっている「はじめてのトポロジー」を紹介します。
どんな本か
「はじめてのトポロジー」は、大学数学のトポロジーを一般の人向けにやさしく解説した本です。
基本的に数式は少なく、「形とはなんだろうか」というお話から始まります。また図が多いので、見ていて楽しいです。
トポロジーにおいては、コーヒーカップとドーナツは全く同じ図形である……という話は有名ですね。
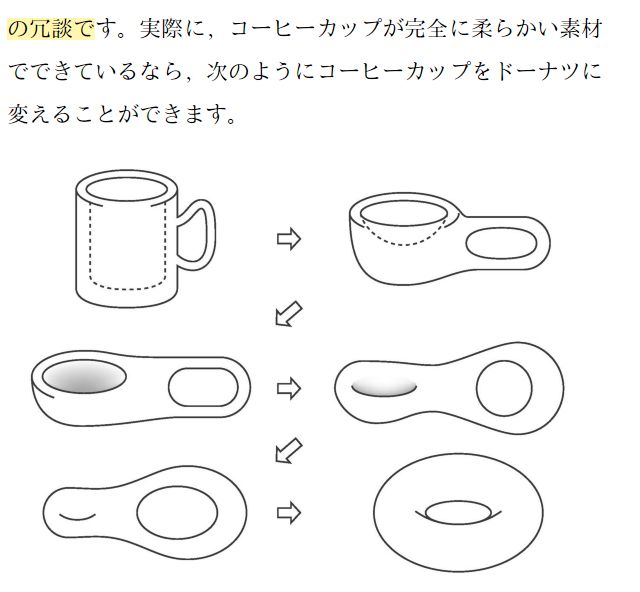
引用:はじめてのトポロジー No.1057
本書の良いところは、入門的な本でありながら、簡単な例を使うことで具体的な計算や論証が身につけられるところです。数学・科学の一般向けの解説本によくありますが、イメージや雰囲気を伝えるばかりで、何も具体的な考え方に踏み込んでいないことがあります。
この本では、ケーニヒスベルクの七つの橋問題を単に紹介するだけではありません。そこからグラフを定義して一筆書きの必要条件を証明したり、グラフの連結性やベッチ数を定義して計算します。定義といっても小学中学生でも理解できる、難しくないものです。この本の具体例を少し変えて自分で考えるのも楽しいと思います。
目次
また、入門的な本でありながら、バランスよく広い話題を扱っているのも良いポイントです。
- 形とはなんだろうか
- つながり方の幾何学
- 曲線のトポロジー
- 曲面のトポロジー
- 曲面のホモロジーとホモトピー
- 次元を超えて
- いろいろな話題
キーワード:グラフ、トーラス、メビウスの帯、クラインの壺、ホモロジー群、ホモトピー、基本群、多様体、ポアンカレ予想、結び目
気になる点
5章から内容を詳しく追うのが結構難しくなります。群の考え方はさらっと紹介されてはいますが、一度触れてみたことがないと理解しにくそうです。とはいえ、専門的な内容から逃げることなく、トポロジーの考え方を示そうとしているのは良いと思います。
また、本格的にトポロジーを学ぶために何をどうやって学べば良いかも、提示されていません。
本書では多くの図を使ってトポロジーの考え方を紹介しましたが、専門の数学書では図がほとんど現れず、ホモロジーやホモトピーが数式で厳密に展開されています。しかし、その背後にはたくさんのイメージが隠されているはずです。
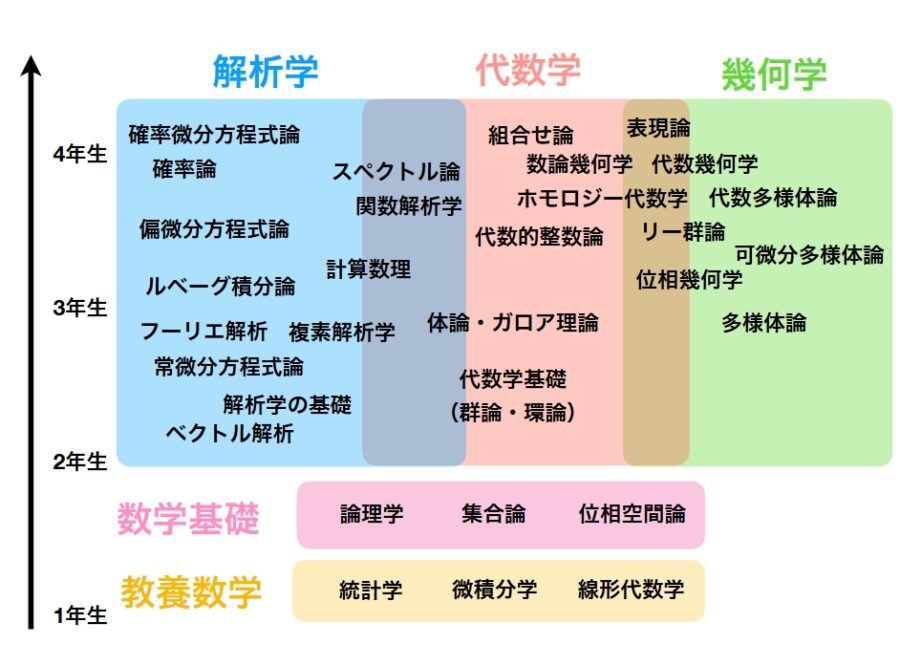
次のロードマップで言えば、代数学基礎、位相空間論、多様体論の予備知識が必要となるでしょう。もしこの本を読んでトポロジーに興味を持ったら、一度トポロジーの専門書をパラパラとめくって、その理解に必要そうなキーワードや分野を逆算的に学ぶのが良いと思います。
僕は「はじめてのトポロジー 」を、Kindleの読み放題サービスKindle Unlimitedで読みました。登録してあれば無料なので、ぜひ試しに読んでみてください。特にグラフの一筆書き問題は、多くの例題を使って遊ぶパズルのようなものなので、トポロジーに親しむのに良いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
PHP研究所 (2009-12-18T00:00:00.000Z)
¥750
森北出版 (2015-04-24T00:00:01Z)
¥2,750
グラフ理論 (Springer‐Verlag GTMシリーズ)
R. ディーステル(著), Diestel,Reinhard(原著), 生也, 根上(翻訳), 克弘, 太田(翻訳)
シュプリンガー・フェアラーク東京 (2000-10T)
¥8,960 (中古品)
遊星社 (2015-05-01T00:00:01Z)
¥2,310
岩波書店 (1992-02-21T00:00:01Z)
¥8,000
こちらもおすすめ
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方






