どうも、木村(@kimu3_slime)です。
前回は、常微分方程式を数値的に解く簡単な方法として、オイラー法・改良オイラー法を紹介しました。
今回は、オイラー法を発展させたより精度の良い解法、ルンゲ=クッタ法を紹介します。
(Pythonでは、Scipyライブラリのintegrate.odeintモジュールで常微分方程式は計算できます。今回は、その原理を学ぶためにも、それらを利用せずに書いてみます。)
ルンゲ=クッタ法の仕組み
求めたいのは、常微分方程式\(\frac{du}{dt}= f(u,t)\)を満たす\(u(t)\)です。
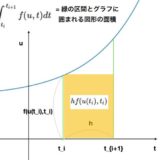
区間\([0,T]\)を等間隔\(h:=\frac{T}{n}\)で分割した点\(t_i := hi,\, i=0,1,\dots,n\)を考えます。分割された区間\([t_i,t_{i+1}]\)で方程式を\(t\)につき積分すると
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+ \int _{t_i} ^{t_{i+1}}f(u,t)dt \end{aligned} \]
です。右辺の積分を長方形で近似したものがオイラー法、台形で近似したものが改良オイラー法でした。
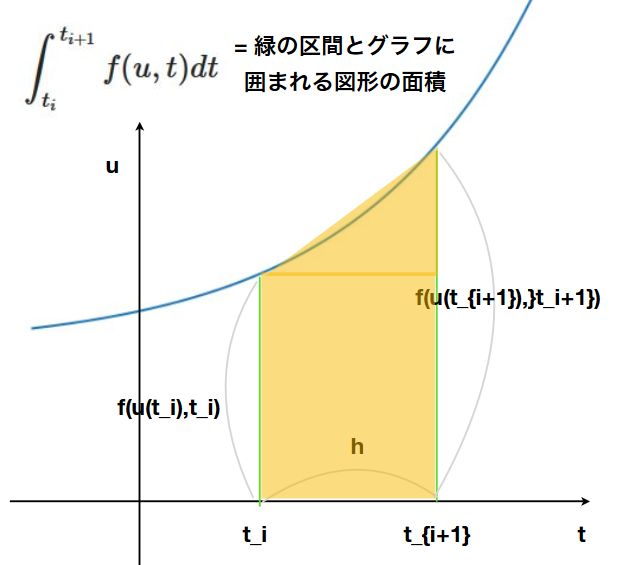
ルンゲ=クッタ法は、これをさらに精度良く改良します。これまでは端点のみの情報でしたが、\(t_i +h/2\)における情報も使って、\(f\)によりフィットする式を考えます。
これまでの方法を、次のように捉え直しましょう。
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+ h f(u(t_i),t_i) \end{aligned} \]
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+\frac{h}{2} \{f(u(t_i),t_i) +f(u(t_{i+1}),t_{i+1}) \}\end{aligned} \]
といった式は、\(k_1 :=h f(u(t_i),t_i) ,\, k_2 :=h f(u(t_i)+k_1,t_i +h)\)と置くことで、
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+ 1\cdot k_1 + 0\cdot k_2\end{aligned} \]
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+\frac{1}{2} k_1 + \frac{1}{2} k_2\end{aligned} \]
と整理できます。
前者は解を1次の項まで、後者は2次の項まで解を近似しているのです。\(u,f\)が微分可能でテイラー展開できたとすると、
\[\begin{aligned} u(t_i + h) &\approx u + h u^{\prime} + \frac{h^2}{2}u^{\prime \prime} \\ &= u + hf + \frac{h^2}{2} (f \frac{\partial f}{\partial u} + \frac{\partial f}{\partial t} ) \end{aligned} \]
となります。一方で、\(k_2\)で2変数のテイラー展開を行えば、
\[\begin{aligned} k_2 &= hf (u(t_i)+ hf, t_i + h) \\ & \approx hf + h^2 (f \frac{\partial f}{\partial u} + \frac{\partial f}{\partial t} ) \end{aligned} \]
となり、1次(2次)の項まで一致していることがわかります。
より一般に、解のテイラー展開の\(r\)次の項まで一致している計算方法は、\(r\)次の精度であると呼ばれます。改良オイラー法が、2次のルンゲ=クッタ法と呼ばれるゆえんです。
計算は大変になりますが、テイラー展開の4次の項まで近似するのが、4次のルンゲ=クッタ法(Runge–Kutta method, RK4)です。これは単にルンゲ=クッタ法と呼ばれます。
\[ \begin{aligned}u(t_{i+1}) =u(t_i)+ \frac{1}{6} (k_1 +2 k_2 + 2k_3 +k_4)\end{aligned} \]
\[ \begin{aligned}k_1 :=h f(u(t_i),t_i) ,\, k_2 :=h f(u(t_i)+k_1 / 2,t_i +h/2)\end{aligned} \]
\[ \begin{aligned}k_3 :=h f(u(t_i)+k_2 / 2,t_i +h/2) ,\, k_4 :=h f(u(t_i)+k_3,t_i +h)\end{aligned} \]
導出の参考:4次のRunge-Kutta法
積分\( \int _{t_i} ^{t_{i+1}}f(u,t)dt\)を、異なる点の情報を使って4パターン\(k_1,k_2,k_3,k_4\)計算したものの重みつき平均として求めた、と言えます。
ルンゲ=クッタ法のプログラム例
オイラー法のときと比較するために、再びマルサスの法則\(f=u\)を考えます。プログラム例は次の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | import numpy as np import matplotlib.pyplot as plt # 区間の分割の設定 T = 50 n = 1000 h = T / n t = np.arange(0,T,h) # 方程式を定める関数、初期値の定義 f = lambda u,t=0 : u #f = lambda u,t=0 : u - u**2 u_0 = 1 #u_0 = 0.1 # 結果を返すための配列の宣言 u = np.empty(n) u[0] = u_0 # 方程式を解くための反復計算 for i in range(n-1): k_1 = h * f(u[i],t[i]) k_2 = h * f(u[i] + k_1 /2 , t[i] + h/2 ) k_3 = h * f(u[i] + k_2 /2 , t[i] + h/2 ) k_4 = h * f(u[i] + k_3 , t[i] + h ) u[i+1] = u[i] + 1/6 * (k_1 + 2*k_2 + 2*k_3 + k_4 ) # 誤差の計算 v = np.empty(n) for i in range(n): v[i] = np.exp(h*i) e = v - u print(v[n-1],e[n-1],e[n-1]/v[n-1]) # グラフで可視化 plt.plot(t,u, label="numerical (RK4)") plt.plot(t,np.exp(t) , label="analytical") #plt.plot(t,1/(1+9*np.exp(-t)) , label="analytical") plt.legend() plt.show() |
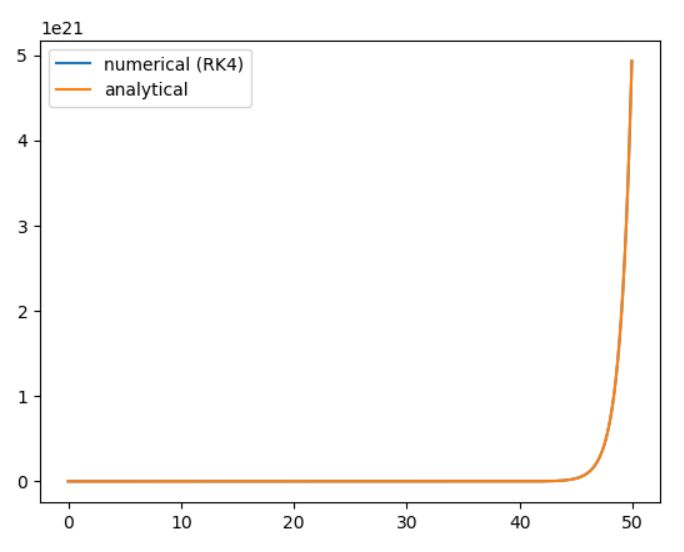
\(t=50\)における絶対誤差は約\(1\times 10 ^{16}\)で、相対誤差は約\(0.0002\)%。
単純なオイラー法では約70%、改良オイラー法では約2%の相対誤差だったので、ルンゲ=クッタ法では相当精度が良くなったことがわかります。
連立常微分方程式を解く:ロトカ・ヴォルテラ方程式
一変数の常微分方程式が解ければ、連立常微分方程式も解けます。
その例として、捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)を解いてみましょう。
\[\begin{aligned} \frac{du}{dt}= u – uv \\ \frac{dv}{dt}= uv – v\end{aligned} \]
プログラム例とその実行結果は次のようになります。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | import numpy as np import matplotlib.pyplot as plt # 区間の分割の設定 T = 50 n = 100000 h = T / n t = np.arange(0,T,h) # 方程式を定める関数、初期値の定義 f = lambda u,v,t=0 : u - u*v g = lambda u,v,t=0 : u*v - v u_0 = 2 v_0 = 1.1 # 結果を返すための配列の宣言 u = np.empty(n) v = np.empty(n) u[0] = u_0 v[0] = v_0 # 方程式を解くための反復計算 for i in range(n-1): k_1 = h * f(u[i],v[i],t[i]) k_2 = h * f(u[i] + k_1 /2 , v[i],t[i] + h/2 ) k_3 = h * f(u[i] + k_2 /2 , v[i],t[i] + h/2 ) k_4 = h * f(u[i] + k_3 , v[i], t[i] + h ) u[i+1] = u[i] + 1/6 * (k_1 + 2*k_2 + 2*k_3 + k_4 ) j_1 = h * g(u[i],v[i],t[i]) j_2 = h * g(u[i], v[i]+ j_1 /2 ,t[i] + h/2 ) j_3 = h * g(u[i], v[i]+ j_2 /2 ,t[i] + h/2 ) j_4 = h * g(u[i], v[i]+ j_3 , t[i] + h ) v[i+1] = v[i] + 1/6 * (j_1 + 2*j_2 + 2*j_3 + j_4 ) # グラフで可視化 plt.plot(t,u, label="u") plt.plot(t,v, label="v") plt.legend() plt.show() |
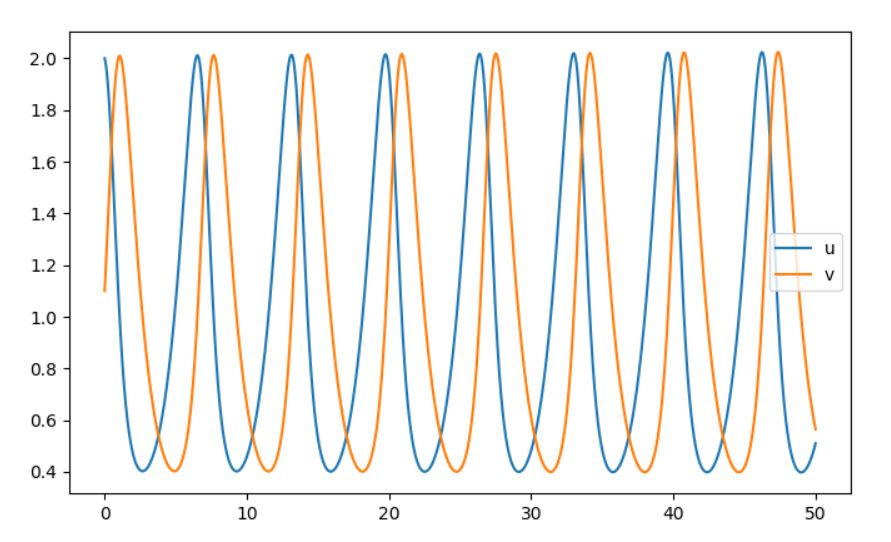
\(u,v\)がいたちごっこのように、増えて減ってを繰り返す、まさに被食者捕食者的な解のようすが読み取れます。
今回、区間の分割数を\(n= 100000\)まで増やしています。\(n = 1000\)程度だと、数値的に不安定で、解は周期的に見えながら\(u,v\)ともに増減が激しくなってしまいました。
今回は、解を4次の項まで近似するルンゲ=クッタ法と、それを使ってロトカ・ヴォルテラ方程式を解くプログラムを紹介しました。
PythonのパッケージScipyのodeintモジュールでは、ルンゲ=クッタ法のほか、 Adams 法(予測子修正子法)、後退微分公式backward differentiation formula (BDF)が使われているようです。
参考:Python NumPy SciPy : 1 階常微分方程式の解法 – org-技術
これで常微分方程式の基本的な数値解法、その考え方やプログラムの書き方は身につけられたのではないでしょうか? 理論的(数学的)に解くのが大変な微分方程式でも、シミュレーションなら近似解が簡単にわかって嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
勾配降下法(Python)でガンマ関数の極小値を調べてみよう
ネイピア数eをPython(decimal)で100桁計算してみよう
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?