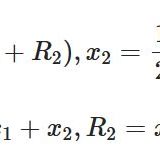どうも、木村(@kimu3_slime)です。
常微分方程式は、ニュートンの運動方程式をはじめとして、マルサスの成長法則、ロジスティック方程式、ロトカ・ヴォルテラ方程式など、科学現象の説明に使われる基本的な方程式のクラスです。
今回は、常微分方程式をコンピュータ、Pythonによるプログラムで解く方法として、オイラー法を紹介します。
(Pythonでは、Scipyライブラリのintegrate.odeintモジュールで常微分方程式は計算できます。今回は、その原理を学ぶためにも、それらを利用せずに書いてみます。)
常微分方程式のおさらい
常微分方程式を解くとは、与えられた関数\(f\)により定まる方程式
\[ \begin{aligned}\frac{du}{dt}= f(u,t)\end{aligned} \]
を満たす関数(=解)\(u(t)\)を求めることでした。初期値\(u_0\)を合わせて考える、すなわち\(u(0)=u_0\)を同時に満たす解は、初期値問題の解と呼ばれます。
例えば、マルサスの法則なら\(f=u\)、ロジスティック方程式なら\(f=ru(1 – \frac{u}{K})\)です。
関数\(f,u\)がベクトル値(\(N\)個の値を持つ)ならば、それは連立常微分方程式と呼ばれます。\(N\)回の微分を含むような微分方程式(\(N\)階の常微分方程式)は、連立常微分方程式にまとめることができます。
そして、連立常微分方程式の解は、各成分毎の常微分方程式の解として得られます。つまり、1次元で1階の常微分方程式が解ければ、多くの方程式が解けることになります。
というわけで、1次元で1階の常微分方程式を数値的に解く方法を考えていきましょう。
オイラー法の仕組み
最も単純な常微分方程式の数値解法として知られているのが、オイラー法(Euler’s method)です。
誤差が大きくなりやすく実用的ではないようですが、単純なため原理を知るには良いので、まずここから始めていきましょう。
求めたいのは、\(\frac{du}{dt}= f(u,t)\)を満たす\(u(t)\)です。ひとまず、\(t\in [0,T]\)としましょう。
コンピュータでは連続的に時間を扱えないので、区間\([0,T]\)を等間隔\(h:=\frac{T}{n}\)で分割した点\(t_i := hi,\, i=0,1,\dots,n\)を考えます。
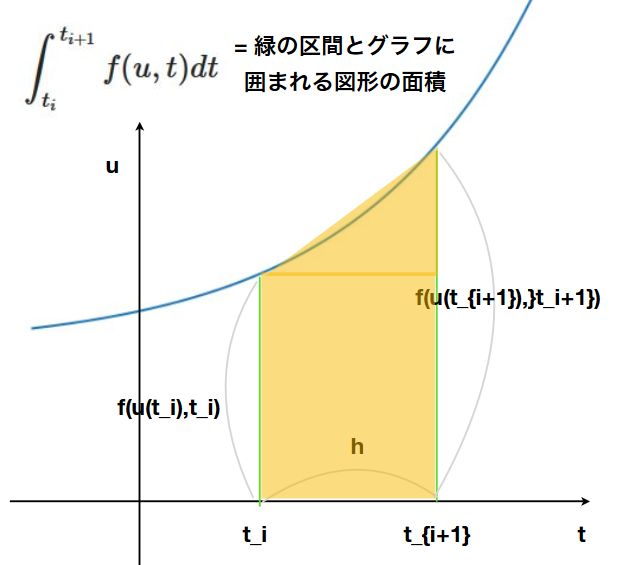
微分方程式を解く基本的な方法は、積分です。分割された区間\([t_i,t_{i+1}]\)で方程式を\(t\)につき積分すると
\[ \begin{aligned}u(t_{i+1})-u(t_i) = \int _{t_i} ^{t_{i+1}}f(u,t)dt \end{aligned} \]
です。もし右辺の積分が計算できれば、\(u(t_0)=u(0)\)から\(u(t_1),u(t_2),\dots\)と順に\(u(t_i)\)が計算できて解が求まります。
オイラー法は、積分を
\[ \begin{aligned}\int _{t_i} ^{t_{i+1}}f(u,t)dt \approx h f(u(t_i),t_i)\end{aligned} \]
として計算する方法です。左側の点を基準に、長方形で近似してしまおうと。なんという雑さ。

方程式全体としては
\[ \begin{aligned}\frac{u(t_i +h)-u(t_i)}{h}\approx f(u(t_i),t_i)\end{aligned} \]
なので、微分を前進差分として近似し、\(f\)を左側の端点で近似したものと言えます。
原理はわかったところで、早速プログラムで見てみましょう。
オイラー法のプログラム例
次のコードが、オイラー法のプログラム例です。区間の設定は、\(T=50,n=1000,h=0.05\)としました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | import numpy as np import matplotlib.pyplot as plt # 区間の分割の設定 T = 50 n = 1000 h = T / n t = np.arange(0,T,h) # 方程式を定める関数、初期値の定義 f = lambda u,t=0 : u #f = lambda u,t=0 : u - u**2 u_0 = 1 #u_0 = 0.1 # 結果を返すための配列の宣言 u = np.empty(n) u[0] = u_0 # 方程式を解くための反復計算 for i in range(n-1): u[i+1] = u[i] + h*f(u[i],t[i]) # u[i+1] = u[i] + h/2 * (f(u[i]) + f(u[i] + h*f(u[i]),t[i]+h) ) """ # 誤差の計算 v = np.empty(n) for i in range(n): v[i] = np.exp(h*i) e = v - u print(v[n-1],e[n-1],e[n-1]/v[n-1]) """ # グラフで可視化 plt.plot(t,u, label="numerical (Euler)") plt.plot(t,np.exp(t) , label="analytical") #plt.plot(t,1/(1+9*np.exp(-t)) , label="analytical") plt.legend() plt.show() |
マルサスの成長モデル
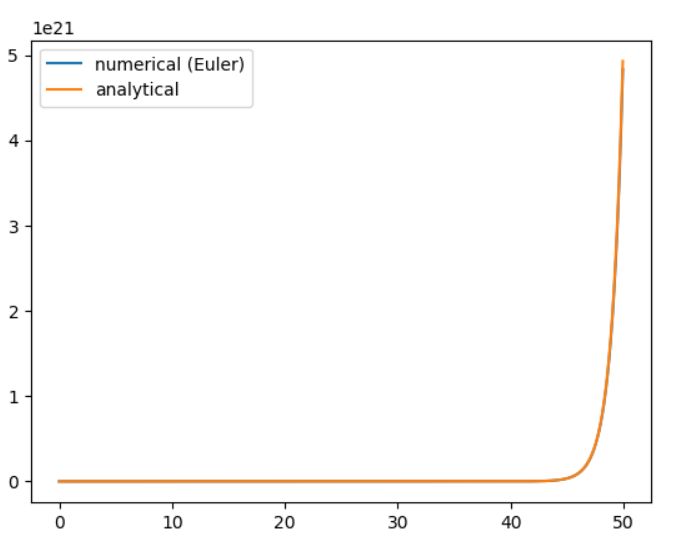
\(f=u\)のときが、マルサスの成長モデルです。数学的な解、すなわち解析解は\(e^t\)とわかっているので、比較した結果は次のようになっています。初期値は\(u_0 =1\)としました。
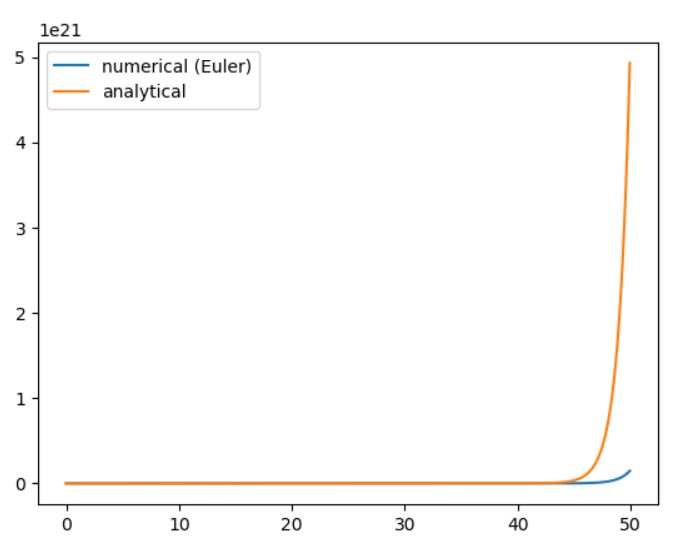
最初のうちは良いのですが、\(t=50\)のところでは約\(4\times10^{21}\)の誤差が出てしまっています。相対誤差は約70%です。マルサスの法則では傾きが大きいため、分割の左側の値だけでは誤差が大きくなってしまうのでしょう。
ロジスティック方程式
\(f=u-u^2\)なるロジスティック方程式を考えました(\(r,K=1\))。解析解は\(1/(1+9e^{-t})\)で、比較した図は次のものです。初期値は\(u_0 =0.1\)としました。
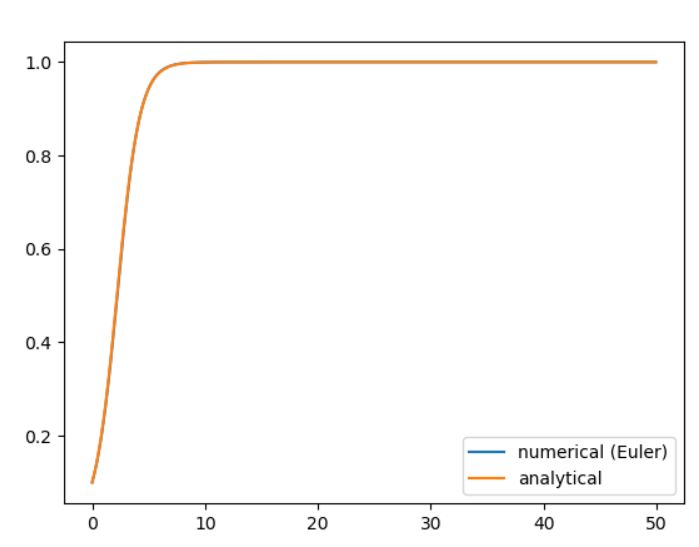
こちらはマルサスの法則と比べ、真の解と数値解の誤差が少ないように見えます。ロジスティック方程式では、解の傾きの大きさ、すなわち\(f\)の絶対値が小さくなっていく(変化量が少なくなっていく)ためでしょう。
改良オイラー法
オイラー法を少し改良したものが、改良オイラー法です。これはホイン法、中点法、2次のルンゲ=クッタ法とも呼ばれます。
単純なオイラー法の問題点は、積分の計算において、\(f\)の左側の値しか用いずに長方形的に近似していることでした。これを両側の点を使って、台形的に近似してみます。
\[ \begin{aligned}\int _{t_i} ^{t_{i+1}}f(u,t)dt \approx \frac{h}{2} \{f(u(t_i),t_i) +f(u(t_{i+1}),t_{i+1}) \}\end{aligned} \]
このままでは積分が\(t_{i+1}\)の言葉で書かれているので、反復計算ができません。そこで、さきほどのオイラー法で用いた近似式、\(u_{i+1}= u_i + h f(u(t_i),t_i)\)を代入すれば、
\[ \begin{aligned}u(t_{i+1}) = u(t_i) + \frac{h}{2} \{f(u(t_i),t_i) +f(u_i + h f(u(t_i),t_i) ,t_i+h) \} \end{aligned} \]
と反復計算できる形になります。これが改良オイラー法です。
そのプログラムは、上で紹介したコードの反復計算の部分で、コメントアウトして既に書かれています。
マルサスモデル\(f=u\)において、数値解と解析解を比較したものが次の図です。
\(t=50\)においては、約\(9\times 10^{19}\)の誤差。相対誤差は約2%で、修正前のオイラー法より、だいぶマシになりました。
今回は、常微分方程式を数値計算する方法として、オイラー法、修正オイラー法を紹介しました。
微分方程式を解くためには積分の値を求める必要がありますが、それを長方形、もしくは台形で近似して計算する方法です。
積分の近似次第で、この方法には改善の余地があります。続いて、オイラー法をより改良した、ルンゲ=クッタ法を紹介しようと思います。
続き:ルンゲ=クッタ法:常微分方程式をPythonで解く原理を解説
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
勾配降下法(Python)でガンマ関数の極小値を調べてみよう
ネイピア数eをPython(decimal)で100桁計算してみよう
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?
ルンゲ=クッタ法:常微分方程式をPythonで解く原理を解説