どうも、木村(@kimu3_slime)です。
今回は、有限群のようすを視覚化する方法、ケーリーグラフと乗積表について紹介します。
ケーリーグラフとは
ケーリーグラフは、有限群の要素間のつながりを視覚化するグラフです。
グラフといっても、関数のグラフではなく、離散グラフ(点とそれを結ぶ辺の集まり)のこと。
グラフ(graph)とは、次を満たす集合の対\(V,E\)です。\(V\)は単に要素の集合で、頂点(vertex)と呼ばれます。\(V\)の異なる二点の組を、\(V\)の辺(edge)と呼び、辺の集まりを\(E\)とします。
早速、具体例を見てみましょう。
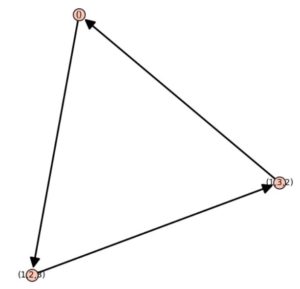
この図において、\(V=\{(),(1,2,3),(1,3,2) \}\)で、\(E=\{ \{(),(1,2,3)\} \{(1,2,3),(1,3,2)\} \{(1,3,2),()\} \}\)です。
ただしここで、\((1,2,3)\)は、1を2に2を3に3を1に移す巡回置換を表しています。\(()=e\)は単位置換、つまり何も入れ替えない置換です。
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説
このグラフは、巡回群\(\mathbb{Z}/3\mathbb{Z}\)のケーリーグラフです。
\(G\)を\(X=\{g_1,\dots,g_n\}\)によって生成される群(有限生成)とします。\(X\)に関する\(G\)のケーリーグラフ(Cayley graph)とは、次のようにして決まるグラフです。\(V=G\)で、\(x,y\)に辺がある条件は、ある元\(g_i\)によって\(y=g_i x\)または\(x=g_i y\)が成り立つこと。
つまり、\(G\)の各要素を頂点とし、生成元をかけることによって移る元を辺でつないだグラフです。
\(\mathbb{Z}/3\mathbb{Z}\)の生成元は\((1,2,3)\)で、\((1,2,3)(1,2,3)=(1,3,2)\)なので辺\(\{(1,2,3),(1,3,2)\}\)があります。他の辺も同様。
ケーリーグラフをSageMathで描く
ケーリーグラフは、手で書くこともできますが、計算ソフトSageMathでも描けます。抽象代数学に関する関数は「Sage Quick Reference: Abstract Algebra」にまとまっています。
ケーリーグラフは、次のようなコードで描けます。
1 2 3 4 | G=CyclicPermutationGroup(3) C=G.cayley_graph() show(C.plot()) g.show3d(color_by_label=True,edge_size=0.01,vertex_size=0.03) |
上のコードでは\(G\)が巡回群ですが、対称群、交代群、二面体群、行列群などの関数が既に用意されています。SageMathは導入も簡単なので、ぜひ試してみてください。
巡回群
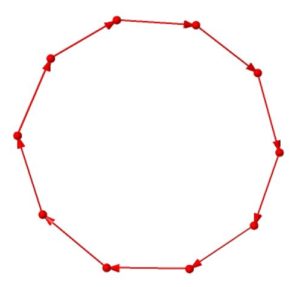
\(\mathbb{Z}/10\mathbb{Z}\)のケーリーグラフは次のようになっていて、巡回群はすべて単純なひとつの輪となっていることがわかります。(グラフに色をつけました)
二面体群
二面体群\(D_2=\langle (1,2),(3,4)\rangle \simeq \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}\)のケーリーグラフは下図。(この群は、クラインの四元数群\(V\)とも同型)
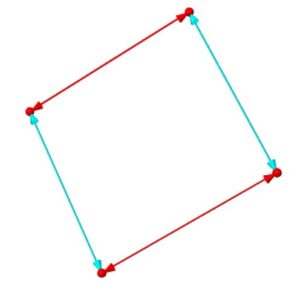
巡回群と見た目は似ていますが、別物です。例えば、赤の頂点の表す要素を2回かけると戻ってきてしまうので、それを何回かけても全体を巡回していません。
\((1,2),(3,4)\)が可換であることが、「赤矢印→青矢印」「青矢印→赤矢印」が等しいことによって表されていることが読み取れます。
\(D_3,D_4\)のケーリーグラフは次のようになります。(\(D_3\)は対称群\(S_3\)と同型)

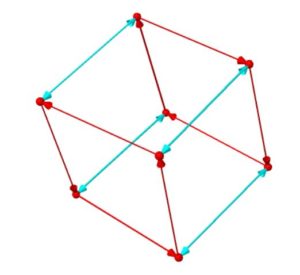
二面体群には、さきほど見た巡回群のようにループになっている部分と、その間を行き来する辺(鏡映)があることが、視覚的にもわかりますね。
交代群
偶置換を集めた交代群\(A_n\)はどうでしょうか。\(A_3\)は巡回群\(\mathbb{Z}/3\mathbb{Z}\)と同型です。\(A_4,A_5\)のケーリーグラフを示します。
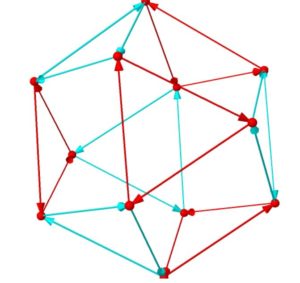
(\(A_5\)は要素が多くてカラー表示できませんでした)
\(A_4\)の一部分からは、四角形のグラフとなっている\(D_2\)が取り出せます。つまり、\(D_2\)は\(A_4\)の(正規)部分群となっていることが、グラフからも読み取れるわけです。
対称群
対称群\(S_3\)のケーリーグラフは、\(D_3\)として見ました。\(S_4,S_5\)はどうでしょうか。
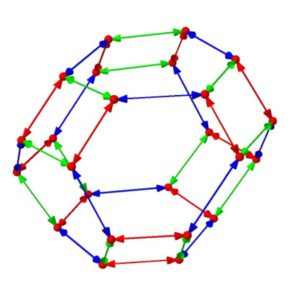

\(S_5\)はわけがわからなくなってしまいました。\(S_4\)の面を増やしたような構造と想像するしかありません。要素数が増えると、素朴な図示では情報を読み取れなくなってしまいます。
乗積表
有限群の要素間の関係をわかりやすく理解する方法として、乗積表(Multiplication table)と呼ばれるものがあります。ケーリーテーブル(Cayley table)、群表とも。
掛け算九九表のように、群の要素を縦と横に並べ、その交差する部分に演算の結果を書くものです。
乗積表もSageMathを使って描けるので、典型例を掲載しておきます。
巡回群
\(\mathbb{Z}/3\mathbb{Z}\simeq A_3\)
二面体群
\(D_2 \simeq V\)
\(D_3\simeq S_3\)
交代群
\(A_4\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | * a b c d e f g h i j k l +------------------------ a| a b c d e f g h i j k l b| b c a f d e h i g l j k c| c a b e f d i g h k l j d| d g j a h k b e l c f i e| e i k c g l a f j b d h f| f h l b i j c d k a e g g| g j d k a h e l b i c f h| h l f j b i d k c g a e i| i k e l c g f j a h b d j| j d g h k a l b e f i c k| k e i g l c j a f d h b l| l f h i j b k c d e g a |
対称群
\(S_4\)
乗積表ならば、ケーリーグラフより詳しく積の関係がわかります。また、表が対称になっている群(\(\mathbb{Z}/3\mathbb{Z},D_2\))は可換で、そうでない群(\(D_3,A_4,S_4\))は非可換であることも読み取れます。
今回は、要素の少ない群を視覚的に捉える方法として、ケーリーグラフと乗積表、そしてそのSageMathを使った表示を紹介しました。
「Group Explorer」というサイトでは、多くの群のケーリーグラフや乗積表をオンライン上で見られます。この記事で紹介しなかった群は多いので、こちらもチェックしてみてください。
「群論の味わい」によると、ルービックキューブの状態は\(S_54\)の部分群として表わせ、その解法はケーリーグラフにおける現在の配置を表す頂点から単位元の頂点への経路として捉えられます。
つまり、ルービックキューブを揃えるための最も少ない手数は、解法の経路のなす距離(最小経路の辺数)です。
群をグラフに対応させるケーリーグラフの考え方は、一般的な数学系の教科書にはあまり載っていませんが、コンピュータを使った群の分析として面白いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
群論の味わい -置換群で解き明かすルービックキューブと15パズル-
共立出版
売り上げランキング: 391,593