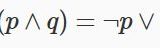「AならばB」は「Aでない、またはB」を真偽値の計算（プログラミング）で確かめる

どうも、木村（@kimu3_slime）です。

論理学・数学において、「AならばB」は「Aでない、またはB」であることを、真偽値の計算（プログラミング）で確かめる方法を紹介します。

「AならばB」は「Aでない、またはB」

「AならばB」は、論理学、そして数学においてよく使われます。「もし仮定Aが正しいならばBが正しい」は、数学の定理の基本的な形です。

このような「ならば」は、論理学の用語としては含意（implication）と呼ばれ、記号では\(\Rightarrow\)と書かれます。

さて、\(A\Rightarrow B\)を否定するとどうなるでしょうか。それは、「AではあるがBではない」、つまり「AかつBでない」です。これを簡単に導くことができるでしょうか？

それは、そもそも「AならばB」が「Aでない、またはB」によって定義されることを知れば明らかです。

すなわち、

\( (A \Rightarrow B) :\Leftrightarrow (\lnot A) \lor B \)

とします。\(\lnot \)は「～でない」（否定）、\(\land \)は「かつ」（論理積）、\(\lor \)は「または」（論理和）です。

右辺が「AならばB」らしい振る舞いをすることを、真偽値の計算（Pythonによるプログラミング）で確かめてみましょう。

コードは次のようになります。

for i in [True, False]:
    for j in [True, False]:
        A = i
        B = j
        print("A, B", A, B)

        P = (not A) or B
        print("P", P, "\n")

for i in [True, False]:

for j in [True, False]:

A = i

B = j

print("A, B", A, B)

P = (not A) or B

print("P", P, "\n")

命題が取る値はTrue（真）,False（偽）のいずれかです。このような値を真偽値、あるいはブール値（boolean value）と言います。

最初のforによって、\(A,B\)が真真、真偽、偽真、偽偽の場合を総当りしています。

そして、\((\lnot A) \lor B\)を\(P\)とおき、その真偽を表示しました。

コードの実行結果は次の通り。

A, B True True
P True 

A, B True False
P False 

A, B False True
P True 

A, B False False
P True

A, B True True

P True

A, B True False

P False

A, B False True

P True

A, B False False

P True

意味を読み取ってみましょう。

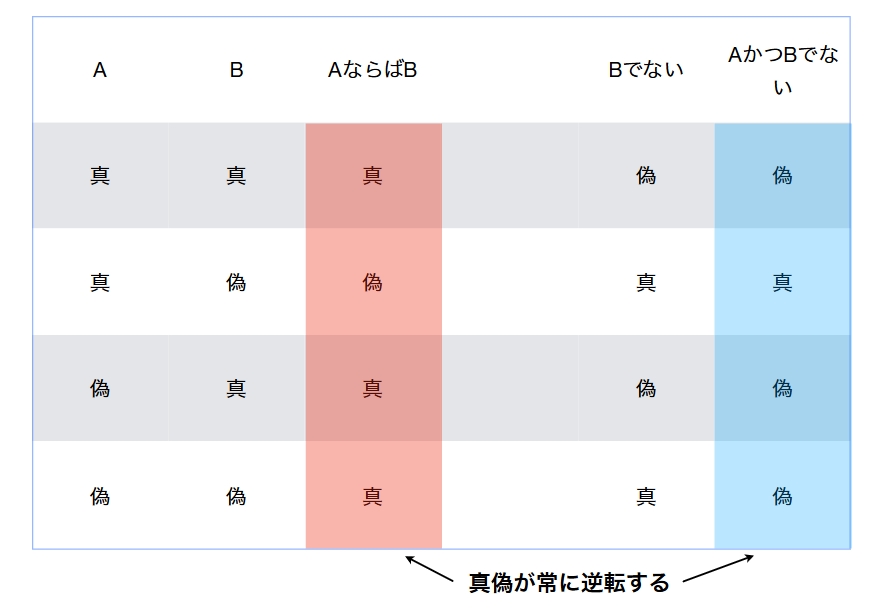
「AならばB」が正しくなるのは、A・Bともに正しいとき。または前提Aが満たされないときです。

「AならばB」が偽になるのは、前提Aが正しいにもかかわらずBが偽のときです。

これらはまさしく「AならばB」の意味するところとマッチしています。図にするとこうです。

一度、「AならばB」の定義

\( (A \Rightarrow B) :\Leftrightarrow (\lnot A) \lor B \)

がのみこめれば、その否定も簡単に導けます。

\(\begin{align*}
\lnot (A \Rightarrow B) & \Leftrightarrow \lnot ( (\lnot A) \lor B ))\\
&\Leftrightarrow \lnot(\lnot A) \land (\lnot B) \\
&\Leftrightarrow A \land (\lnot B) \\
\end{align*}\)

途中の変形に、ド・モルガンの法則を使いました。

つまり、「AならばB」の否定は、「Aでない、かつB」です。

「AならばB」が「Aでない、またはB」によって定義されることが納得できたでしょうか。「ならば」（含意）は、否定と論理和の組み合わせで表せるのです。

こうした論理の扱いに慣れれば、込み入った数学の議論でも迷いなく論理を追いやすくなるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。