どうも、木村(@kimu3_slime)です。
物が燃える現象、燃焼反応は、物質と酸素の化学反応であり、数学では反応拡散方程式として表されます。
今回は、燃焼反応に関連したモデルで起こる、解の爆発と呼ばれる現象について紹介します。
数式を交えますが、わからなくても大丈夫。雰囲気だけ感じ取っていただければ嬉しいです。
反応拡散方程式、燃焼反応、藤田方程式
反応拡散方程式は、次のように表されます。
\[ \begin{aligned}\frac{\partial u}{\partial t} = \Delta u + f(u)\end{aligned} \]
\(u(x,t)\)は温度(または物質の濃度)で、\(\Delta u\)は拡散項、\(f(u)\)は反応項と呼ばれます。
\(f(u)=0\)のときは、熱や粒子の拡散を表す熱方程式(拡散方程式)ですが、反応拡散方程式では0でない場合を考えます。
参考:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、花粉の広がりを数式で予測する、拡散方程式とは
燃焼反応では、アレニウスの法則により、\(f(u)=e^{-\frac{1}{u}}\)という形になると言われています。
参考:Mathematical Problems from Combustion Theory
このタイプの反応項は、数学的に扱うのが少し難しくなります。そこで、この反応から少し派生した次のような方程式を考えましょう。
\[ \begin{aligned}\frac{\partial u}{\partial t} = \Delta u + u ^p , \quad p>1\end{aligned} \]
式の導出について参考:非線形熱方程式の爆発問題入門—Marek Fila氏講義録—
この方程式は、それを先駆的に研究した数学者・藤田宏の名前を取って、藤田方程式と呼ばれています。
解の爆発とは?
解の爆発と呼ばれる現象を紹介しましょう。
藤田方程式から拡散項を消した常微分方程式を考えてみます。これは、加熱反応しか起こらない方程式です。
\[ \begin{aligned}\frac{du}{d t} = u ^p\end{aligned} \]
初期値\(u_0 >0\)に対応する解は、
\[ \begin{aligned}u(t) = \frac{1}{( \frac{1}{u_0 ^{p-1}} – (p-1)t)^{p-1}}\end{aligned} \]
で、有限時間\(T= 1/\{ (p-1) u_0 ^{p-1}\}\)で解は無限大に発散します。
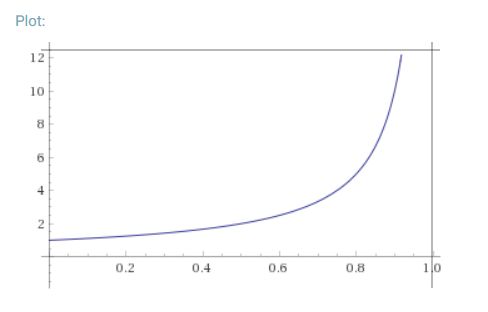
画像引用:wolframalpha
このような現象を解の爆発(blow-up)といい、その時間を爆発時刻と呼びます。逆に、爆発せずに存在し続ける解は、時間大域解と呼ばれるものです。
拡散項を加えた方程式でも、その最大値(\(L ^ \infty\)ノルム)が無限大に発散するとき、解の爆発と呼びましょう。
一般に、拡散項は解をなめらかに、平らにしていく効果があります。
藤田方程式は、拡散と反応の効果により、爆発解とそうでない解、両方が見られることがあります。どんな条件で、爆発は起こるのでしょうか?
じつは、指数\(p\)により、解の性質が大きく変わることが知られています。次の結果です。
\[ \begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial u}{\partial t} &= \Delta u + u^p \quad & x \in \mathbb{R}^N,t>0\\ u(x,0) &= u_0(x) \quad & x \in \mathbb{R}^N \\ \end{array} \right.\end{aligned} \]
初期値\(u_0\)は連続で、正値(\(u_0 \geq0, u_0 \not\equiv 0\))とする。(最大値原理より、解は\(t>0\)で正となることが保証されています。)
\(p_F:= \frac{N+2}{N}\)とする。
正値解について、
(i) \(1<p<p_F\)ならば、すべての解は有限時間で爆発する。
(ii) \(p_F <p\)ならば、時間大域解が存在する。
元論文:H. Fujita, On the blowing up of solutions of the Cauchy problem for \(u_1+\Delta u+u^{1+\alpha}\) (1966)
この指数\(p_F\)は、藤田指数(Fujita exponent)と呼ばれています。
面白いのは、指数\(p\)によって解のようすがガラッと変わってしまうことです。
\(p\)が大きい方が解が爆発しやすそうな気がしますが、違います。正値解が爆発するためには、小さい解\(0\leq u<1\)が爆発することが重要です(比較定理より、小さい解が爆発すればより大きい解は爆発する)。\(0\leq u<1\)のとき、反応項\(u^p\)は\(p\)が小さいほど強く働くのです。
指数\(p_F\)は、空間の次元\(N\)が大きくなるほど小さくなる、つまり爆発が起こりにくくなります。これは次元が上がるほど、拡散の方向が増えて効果が大きくなるためと考えられます。
このような解の爆発現象に関しては、爆発の条件、爆発時刻、爆発する点の集合、爆発の速さ、爆発するときの解の形状などについて、多くの研究がなされています。
拡散と反応を合わせた反応拡散方程式では、熱方程式では起こらない多様な現象が見られ、解の爆発はそのひとつです。
燃焼反応に関連するモデルとして見れる藤田方程式では、指数\(p\)の大きさによって爆発するかしないかが変わってくる、劇的な変化が見られます。
「爆発は何が原因で起こっているのかか?」「爆発するときに何が起こっているのか?」そんな問題に、数学からアプローチすることもできるのは、面白いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Mathematical Problems from Combustion Theory (Applied Mathematical Sciences)
Springer
売り上げランキング: 237,933
東京大学出版会
売り上げランキング: 989,417