どうも、木村(@kimu3_slime)です。
常微分方程式の教科書や授業は、どうもその解き方に焦点が当たりがちで、何の応用があるのかわかりにくい印象があります。
きっと、応用例は他のそれぞれの分野に任せ、数学の授業としては一般論をカバーする……あるいは、応用例は紙面の余裕がないし、微分方程式の本質に関係しない……ということなのでしょう。それでも、無機的に解き方を覚えるよりは、同時にその使いみちを知った方が深い理解につながるのではないでしょうか。
今回は、熱方程式を解くことを考えると、自然と2階線形常微分方程式が出てくることを紹介します。
2階線形常微分方程式の一般解
2階線形常微分方程式とは、\(a,b \in \mathbb{R}\)を定数として
\[ \begin{aligned}y^{\prime \prime} + ay’ +by =0\end{aligned} \]
と表される常微分方程式のことです。
2階とは、方程式の中に最大で2回の微分が登場すること。線形とは、\(y_1,y_2\)を任意の解とすると、\(C_1 y_1 + C_2 y_2\)も解となるような性質のことです。
この方程式の一般の解は、特性方程式(characteristic equation)と呼ばれる方程式
\[ \begin{aligned}\lambda ^2 + a\lambda +b =0 \end{aligned} \]
の解\(\lambda_1,\lambda_2\)を用いて、次のように表されることが知られています。
i) \(\lambda_1 \neq \lambda_2 , \lambda_1, \lambda_2 \in \mathbb{R}\)のとき
\[ \begin{aligned}y = C_1 e^{\lambda_1 x} +C_2 e^{\lambda_2 x}\end{aligned} \]
ii) \(\lambda_1 = \lambda_2\)のとき
\[ \begin{aligned} y= e^{\lambda_1 x} (C_1 + C_2 x)\end{aligned} \]
iii) \(\lambda_1 = p +qi, \lambda_2 = p- qi , p,q \in \mathbb{R}\)のとき
\[ \begin{aligned} y= e^{p x} (C_1 \cos {qx} + C_2 \sin {qx })\end{aligned} \]
特性方程式が導かれる理由を簡単に紹介しましょう。
\(D= \frac{d}{dx}\)と置き(微分演算子)、微分方程式を書き換えると
\[ \begin{aligned}(D ^2 + a D +b) y =0\end{aligned} \]
です。微分作用素と定数は順序交換できるので、\(D ^2 + a D +b\)を\(D\)に関する2次方程式と見て因数分解してみましょう。
解を\(\lambda_1 ,\lambda_2\)とすると、
\[ \begin{aligned} (D – \lambda_1 )(D- \lambda_2) y =0\end{aligned} \]
となります。ここで、\(a = -(\lambda_1 + \lambda_2) ,b= \lambda_1 \lambda_2\)です。
2次方程式の解と係数の関係により、\(\lambda_1, \lambda_2\)は特性方程式を満たすものです。
そして、因数分解された式\( (D – \lambda_1 )(D- \lambda_2) y =0\)は扱いやすく、両辺に順次\(e^{-\lambda_1 x} ,e^{-\lambda_2 x} \)をかけて積分することで、一般解
\[ \begin{aligned}y = C_1 e^{\lambda_1 x} +C_2 e^{\lambda_2 x}\end{aligned} \]
が求められます(\(\lambda_1 \neq \lambda_2\)のとき)。
このような方法を、(微分)演算子法と呼びます。詳しくは、微分方程式の教科書、例えば柳田-栄「常微分方程式論」を参照。
熱方程式から導かれる2階線形常微分方程式
熱方程式(拡散方程式)は、熱や粒子が時間経過とともに広がっていく現象を表した偏微分方程式です。
参考:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、花粉の広がりを数式で予測する、拡散方程式とは
これを解くときに、2階線形常微分方程式が登場します。
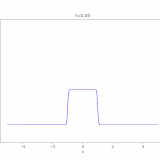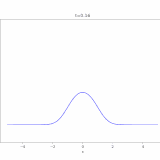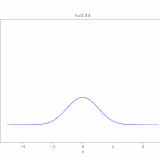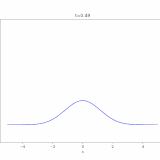
1次元の区間\([0,1]\subset \mathbb{R}\)における次のような熱方程式を考えます。
\[ \begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial u}{\partial t} &= \Delta u \quad & \text{in } (0,1)\times (0,\infty) \\ u &= 0& \text{on } \{x=0,1\}\times [0,\infty) \\ u &= g& \text{on } (0,1)\times \{t=0\} \\ \end{array} \right. \end{aligned} \]
ここで、\(\Delta u = \frac{\partial ^2 u}{\partial x^2}\)です。
解\(u\)が\(u(x,t)=v(t)w(x)\)と変数\(x,t\)が分かれているように表せたとして、関数\(v,w\)が求めてみましょう(変数分離法)。
変数が分離しているので、偏微分が簡単に計算できて、
\[ \begin{aligned} v'(t) w(x) = v(t) \Delta w (x)\end{aligned} \]
となり、\(v(t),w(x)\neq0\)となる\(x,t\)に対して割ると
\[ \begin{aligned} \frac{v'(t)}{v(t)} = \frac{ \Delta w (x)}{w(x)}\end{aligned} \]
です。
左辺は\(t\)のみの、右辺は\(x\)のみの関数にもかかわらず、これらが常に等しくなっているので、両辺は定数です。
そこで定数を\(\lambda\)とすると、
\[ \begin{aligned}v’ = \lambda v\end{aligned} \]
\[ \begin{aligned}\Delta w = \lambda w\end{aligned} \]
です。
上の方程式は一階の常微分方程式で、その解は \(v = C e^{\lambda t}\)です。
下の方程式が、二階の線形常微分方程式です。書き方を変えると、
\[ \begin{aligned}w^{\prime \prime} – \lambda w = 0\end{aligned} \]
で、\(a=0,b= -\lambda\)と対応しています。
上で紹介した線形常微分方程式の解き方により、特性方程式の解は\(\pm \sqrt{\lambda}\)なので、方程式の解は
\[ \begin{aligned} w(x) = \left\{ \begin{array}{l} C_1 e^{\sqrt{\lambda} x} + C_2 e^{\sqrt{-\lambda}x} & \lambda>0 \\ C_1 + C_2 x & \lambda =0 \\ C_1 \cos{\sqrt{-\lambda}x } + C_2 \sin {\sqrt{-\lambda}x } & \lambda <0 \end{array} \right. \end{aligned} \]
と求められます。
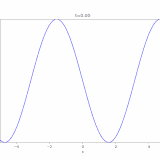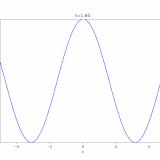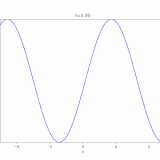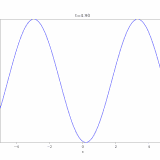
今回の方程式では、境界条件により、\(\lambda <0\)となって、\(w(x)= C_2 \sin n\pi x\)となります。
参考:熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)
一般に、
\[ \begin{aligned}w^{\prime \prime}= \lambda w \end{aligned} \]
\[ \begin{aligned}\Delta w = \lambda w\end{aligned} \]
という問題を、(ラプラシアン\(\Delta\)の)固有値問題と呼びます。
2階線形常微分方程式
\[ \begin{aligned}y^{\prime \prime} + ay’ +by =0\end{aligned} \]
というクラスは、\(a=0,b= -\lambda\)として、固有値問題を含んでいるわけです。
1次元の偏微分方程式(例:熱方程式)を解くことが、1次元の固有値問題に帰着され、それを2階線形常微分方程式の一般論で解くことができる。
この例を通して、2階線形常微分方程式を学ぶ意味を感じ取ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
朝倉書店
売り上げランキング: 236,150
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)