数学・科学における「線形・非線形」の違いを詳しく解説

どうも、木村（@kimu3_slime）です。

数学、科学全般に登場する「線形・非線形」という用語を、詳しく解説します。

この言葉を理解するポイントは、「何が」線形・非線形なのか意識することです。順に見ていきましょう。

数学に登場する「線形・非線形」
科学全般に登場する「線形・非線形」

数学に登場する「線形・非線形」

最初に、数学に登場する「線形」、線形関数、線形空間、線形方程式について紹介します。

関数が線形・非線形

最もシンプルかつ根源的なのが、関数が線形・非線形という話です。

砕けた言い方をすれば、グラフが直線形になる関数が線形関数で、そうでない関数が非線形関数です。

線形な関数の例 \(f(x)=x,2x,Ax\)
非線形な関数の例 \(f(x)=x^2,\sin x, e^x, \log x\)

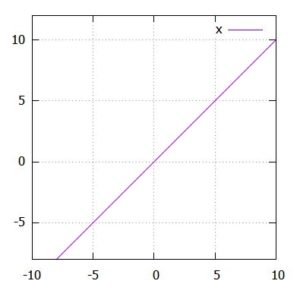
より正確には、関数\(f\)が線形（linear）であるとは、

加法性（additivity）任意の\(x,y\)に対して、\(f(x+y)=f(x)+f(y)\)
斉次性（homogeneity）任意の\(x\)、任意のスカラー\(k\)に対して、\(f(kx)=kf(x)\)

の両方が成立することです。

\(f(x)=2x\)は、加法性と斉次性を明らかに満たし、線形です。\(f(x)=x^2\)は線形ではありません。\(f(1+1)=4\neq 2= f(1)+f(1)\)なので。

関数が線形であることを、関数が線形性（linearity）を持つ、とも言います。

\(A\)を\(N\)次正方行列、\(x\in \mathbb{R}^N\)として、\(f(x)=Ax\)と定めると、\(f\)は線形関数です。これは行列の線形性によるものです。

逆に、\(x\in \mathbb{R}^N\)を変数とする一般の関数\(f\)が線形性を持つとき、それを行列によって表現することができます（これを表現行列という）。

\(f(x)=Ax\)をベクトルの変換として見るとき、これは線形変換（一次変換）とも呼ばれます。

関数\(f\)の変数\(x\)が、数やベクトル以外、例えば数列や関数のときにも、線形性の定義は同じです。

線形な写像は線形写像、線形な作用素は線形作用素（線形汎関数）と呼ばれます。例えば（単純な）微分作用素や積分作用素は、線形作用素です。

空間が線形・非線形

\(n\)次元のベクトルを集めたユークリッド空間\(\mathbb{R}^N\)は、線形空間（ベクトル空間）の一例です。

また、直線や平面といった集合は、（高次の）ユークリッド空間の線型部分空間となっています。ざっくり言えば、和やスカラー倍について閉じていて、線形に見える対象です。

より一般には、集合\(V\)が体\(K\)上の線形空間（linear space）とは、

和と呼ばれる演算が定まり、\(V\)が和について可換群
スカラー倍と呼ばれる演算が定まり、\(x,y\in V, \lambda,\mu \in K\)に対し
\[ \begin{aligned}(\lambda+\mu)x = \lambda x + \mu x \\ \lambda (x+y)= \lambda x+ \lambda y \\ (\lambda \mu)x= \lambda (\mu x) \\ 1x=x\end{aligned} \]

が成立することと定義されます。

線形空間は、ユークリッド空間の性質を取り出して一般化したものと言えます。

例としては、（一定のサイズの）行列全体のなす集合、連続関数全体のなす集合、\(K\)係数の多項式の全体、1次方程式の解の集合、線形微分方程式の解の集合などは、線形空間です。

線形空間のいくつかのベクトル\(x_1,\dots,x_k\)をスカラー倍でつなぎあわせたベクトル\(\lambda_1 x_1 +\dots+ \lambda _k x_k\)は、ベクトルの線形結合（linear combination）と呼ばれるものです。複数のベクトルの線形結合全体を集めた集合は、部分線形空間となります。

参考：基礎講義線形代数学

方程式が線形・非線形

物理現象、自然現象を説明する微分方程式ですが、線形微分方程式と非線形微分方程式に分類されています。

簡単な例で言えば、バネの運動方程式は線形方程式です。

\[ \begin{aligned} m \frac{d^2 x}{dt^2} = – kx\end{aligned} \]

一方で、振り子の運動方程式は非線形方程式です。

\[ \begin{aligned} m \frac{d^2 x}{dt^2} = – k \sin x\end{aligned} \]

線形方程式の特徴は、解の重ね合わせの原理（superposition principle）が成り立つことです。

つまり、\(x_1,x_2\)を方程式の解、\(\lambda\)を定数とするとき、\(x_1+x_2\)も解、\(\lambda x_1\)も解となる。

重ね合わせの原理が成立する方程式を、線形方程式と呼びます。そうでない方程式が、非線形方程式です。

重ね合わせの原理は、これまで説明してきた関数、空間の線形性によっても表現できます。

つまり、方程式を作用素\(F\)によって\(F=0\)となる形に表し、\(F\)が線形作用素となるとき、方程式は線形である。また、方程式の解のなす集合が線形空間となるとき、方程式は線形である。こう言っても同じです。

熱の伝搬や粒子の拡散を説明する、熱伝導方程式（拡散方程式）は線形偏微分方程式です。

\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u\end{aligned} \]

一方で、化学物質の化学反応と拡散を説明する、反応拡散方程式は、非線形偏微分方程式です。

\[ \begin{aligned}\frac{\partial u}{\partial t}= \Delta u + f(u)\end{aligned} \]

参考：花粉の広がりを数式で予測する、拡散方程式とは、生き物の模様は数式で決まる？チューリング・パターンとは

微分方程式が線形だと、多くの場合は解の存在と一意性が保証され、明示的に解を得る手法が広く知られています。（ただし、偏微分方程式においては、線形であっても解が存在しないものが知られています。参考：Lewy’s example – Wikipedia）

常微分方程式の教科書では、まずは線形状微分方程式の解放を学ぶことになるでしょう。

一方、非線形微分方程式では、解の存在と一意性すらわからないものも存在します。

例えば、流体の運動を記述する（3次元）ナビエ・ストークス方程式の解の存在となめらかさは、ミレニアム問題と呼ばれる今なお未解決の難問です。

また、解の存在と一意性が保証されたとしても、解が明示的な形（わかりやすい計算式）で表示できるとは限りません。そのため、解の表示式を得ずとも解の挙動を調べようとする、力学系理論という分野が生まれてきました。

参考：惑星の運動は数学的に「解けない」？　多体問題から力学系理論へ

総じて、線形方程式は数学的に扱いやすいけれども表す現象が単純で、非線形微分方程式は表す現象が豊かだが扱いにくい、という関係性にあります。

科学全般に登場する「線形・非線形」

数学における「線形」の概念をベースにして、科学全般に線形という用語は使われています。

線形構造解析と非線形構造解析

機械や構造物に負荷がかかったときの変形を扱う材料力学では、非線形構造解析という用語があります。

ひずみによって大きな変形が起こるときは幾何学的非線形性、金属材料を例としたひずみと応力の間の材料非線形性、滑りや摩擦といった境界の非線形性などがキーワードです。

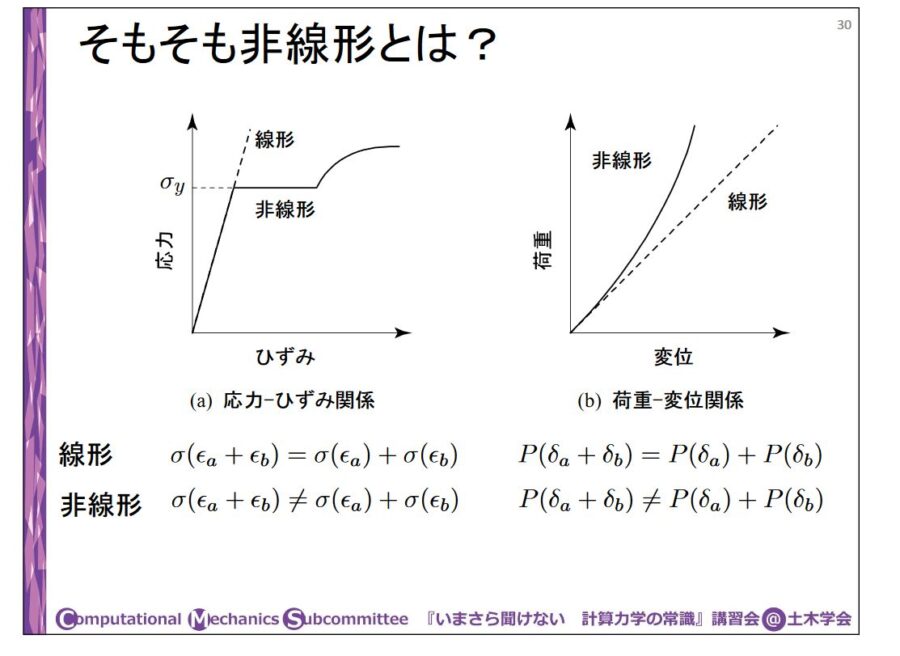
画像引用：構造解析に入る前に知っておきたい「常識」 – 土木学会

参考：3. 線形解析と非線形解析の違い – FASOTEC

線形システム

線形システムとは、一般には、連立線形微分方程式のことです。

特に制御工学の一分野として、線形システムを使ってその安定性や可制御性を調べる分野は、線形システム論と呼ばれています。

一方、非線形システムを対象とする場合、非線形子システム論と呼ばれます。

制御工学は、例えば自動運転車の制御などに応用できますね。

参考：線形システム論 I. 概論、非線形システムの表現 – システム制御理論研究室 – 北海道大学、自動運転今昔物語 – 自動車技術会

線形回帰・非線形回帰

統計学には、回帰理論と呼ばれるものがあります。

例えば、年齢と収入に関する離散的なデータがあったとして、それらをできるだけ誤差なく結びつける連続的な関数（モデル）を得るのが回帰分析です。

そして直線的な関数（線形関数）によって説明しようとするのが、線形回帰。そうでなく、多項式関数などを使って回帰を行うのが非線形回帰です。

参考：【初心者大歓迎!】線形回帰分析入門 ~ 最小二乗法から決定係数まで – Np-Urのデータ分析教室

非線形現象、非線形数理、非線形科学

非線形現象とは、非線形な方程式によって表される自然現象全般を指す言葉です。

自然現象をより正確に記述しようとすれば、ほとんどの現象は非線形現象と言えますが、あえて非線形現象というときは、次に紹介するような非線形特有の現象を指しています。

パターン形成
リズム現象、同期現象
カオス、分岐現象
爆発現象

参考：カオス理論、バタフライ・エフェクトとは何か？ローレンツ・アトラクターを例に

非線形現象を扱う数理科学は非線形数理、またその科学全般は非線形科学と呼ばれています。特にコンピュータの発展、シミュレーションと視覚化により、注目を集めるようになってきた分野です。

こうして「非線形」という用語が一般に飛び出すと、「1+1=2にならない世界」といったよくわからない説明が見られることがあります。

今回紹介したように、数学用語としての「線形」の意味を抑えて、「何が」線形なのかわかれば、一般に使われる「非線形」に惑わされることもなくなるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。