どうも、木村(@kimu3_slime)です。
「惑星の運動はいつまでも安定なのか?」を調べていくと、「それを記述する方程式は解けない」ことがわかった、という話をしました。
解けなくてもなんとか方程式の解の情報が知りたい、それが力学系の理論です。
今回は、解の安定性をテーマに力学系の理論を紹介したいと思います。
微分方程式に関する基礎知識はこちら:「運動」をイメージすればわかる、微分と積分入門、サイン、コサインは何の役に立つ? バネの振動と三角関数
解の軌跡を見てみよう
力学系の理論では、解が時間変化によって空間の中で描く軌跡(orbit,trajectory)にまず注目します。
試しに、バネの運動方程式を考えてみましょう。
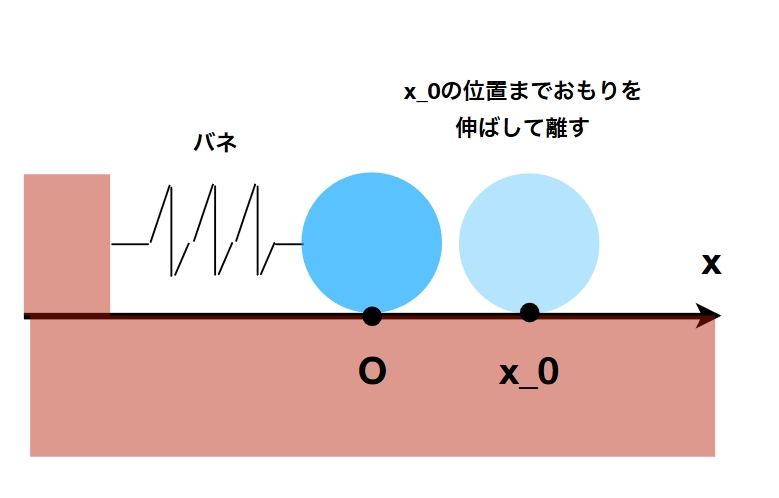
時刻\(t\)におけるおもりの位置を\(x(t)\in\mathbb{R}\)とし、簡単のため\(m=1,k=1\)のときを考えると
\[ \begin{aligned}\frac{d^2 x}{dt^2}= -x\end{aligned} \]
となります。この方程式を図示しやすくするために、\(y=\frac{d x}{dt}\)とおくと、
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} =-x \end{array} \right.\end{aligned} \]
という連立微分方程式になります。これを\(x-y\)平面に描いたのが下図です。
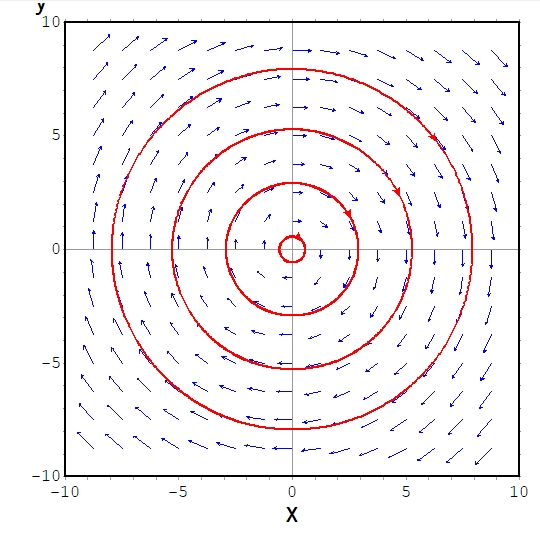
青い矢印は解が時間変化によって向かう方向を示しています。(点\((x,y)\)におけるベクトルは、\((y,-x)^T\)で決まっています。)
例えば、\(y=0,x=1\)となる点からスタートしてみましょう。矢印に沿って動かすと、時計まわりにぐるぐると回りますね。図を見ると、位置\(x\)は右から左へ動いた後、左から右へ戻ってきます。また速度\(y\)は早くなったり遅くなったりします。(\(x,y\)がマイナスであるときは、おもりが基準点から左側にある、向かっていることを意味しています。)
この周期的な運動は、まさしくバネの運動ですね。ほかのさまざまな点からスタートしてイメージしてみてください。
方程式によって決まるこのような図を、相図(phase portrait)または相空間(phase space)と言い、解の時間変化を示す赤い曲線を解曲線と言います。
相図を見れば、解がおよそどんな動きをするのか検討をつけられます。しかも、方程式を解いて解の表示式を得ていない(解いていない)にもかかわらず、です。
以前記事で紹介した「ローレンツ・アトラクター」も、相空間に解の軌跡を描いたものです。

画像引用:Chaos7 Attracteurs étranges : L’effet papillon
力学系の理論では、まず微分方程式に対応する相図をイメージし、それがどのような特徴を持っているか分析していきます。分析すべき特徴のひとつが、次に紹介する安定性の話です。
平衡解の安定性
相図の特徴をつかむには、特殊な解を調べるのが良いでしょう。
そのひとつが、平衡解(equilibrium solution)と呼ばれる時間変化しない解です。
難しいことはありません、バネの方程式では、停止状態\((x(t),y(t))=(0,0)\)は平衡解です。平衡解は、物理的には定常状態(steady state)とも呼ばれます。数学的には、不動点・固定点(fixed point)、臨界点(critical point)とも呼ばれますね。
つりあいの取れた状態はきちんと続くのか。これは、力学系の理論では平衡解の安定性と呼ばれる問題です。
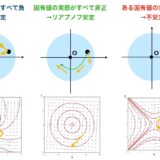
(リアプノフの意味で)安定
バネ運動の相図を見てみましょう。
原点は解です。原点の付近の解を見てみると、どんなに時間が経っても、そこから離れることはありません(一定距離を保ち続けています)。

このようなとき、平衡解は(リアプノフの意味で)安定(Lyapunov stable)であると言います。平衡解から初期状態が少し変わっても、解は離れていかないという意味での安定性を意味しています。
漸近安定
運動方程式の例からはなれ、いろいろな微分方程式の相図を見てみましょう。
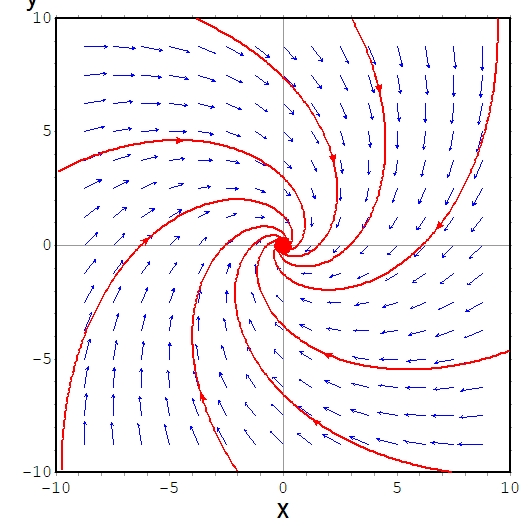
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-x+y \\ \frac{dy}{dt} =-x-y \end{array} \right.\end{aligned} \]
この方程式において、\((x(t),y(t))=(0,0)\)は平衡解です。
そして、平衡解のまわりの解は、時間が経てばすべて平衡解に向かっていきます。このような平衡解を、漸近安定(asymptotically stable)と言います。
リアプノフの意味での安定性は「離れない」という消極的なものでしたが、漸近安定性は「近づいていく」という強いものです。
平衡解が漸近安定ならばリアプノフ安定です。しかし、バネの運動の例のように、リアプノフ安定だからといって漸近安定とは限りません。
不安定
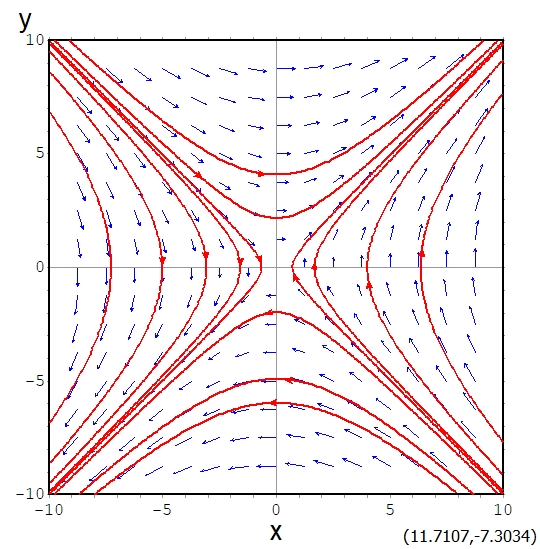
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =y \\ \frac{dy}{dt} = x \end{array} \right.\end{aligned} \]
この方程式においても、\((x(t),y(t))=(0,0)\)は平衡解です。
しかし、平衡解のまわりの解を考えると、平衡解から遠ざかっていくものがたくさんあります。
平衡解のどんなに近くにも遠くに遠ざかっていく解があるとき、平衡解は不安定(unstable)であるといいます。
上の相図とは少し状況が違いますが、単振り子の運動では不安定な平衡解があります。ちょうど真上に振り子を経てた状態というのは確かにありますが、それはほんのちょっと揺らせば下側へ向かってしまい戻ってきません。
安定性まとめ
リアプノフ安定、漸近安定、不安定という3つの安定性に関する概念を紹介しました。
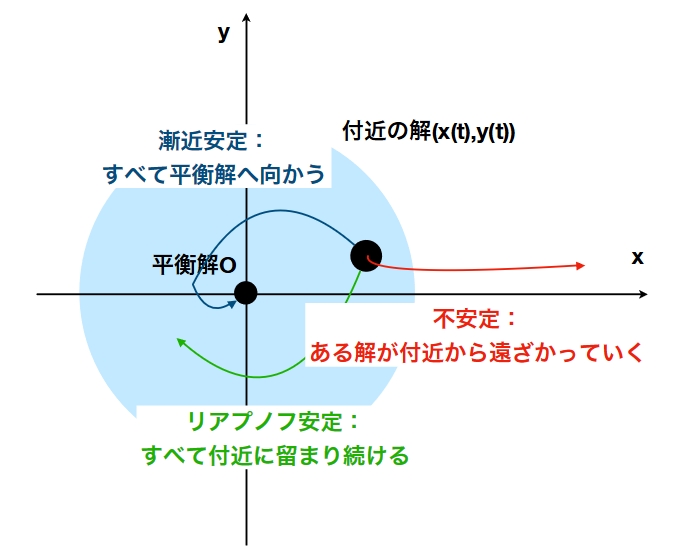
安定性とは、平衡解という状態からちょっとずれたときの解の挙動を調べましょうという話です。
ちょっとずれただけで戻らなくなるなら不安定、離れていかないならリアプノフ安定、戻っていくなら漸近安定という区分でした。
力学系の理論は、方程式を解かずに、解の挙動(例えば安定性)を調べるものだ、ということが感じられたでしょうか?
次の記事では、線形代数の固有値という考え方で、解の安定性を判別する方法を紹介したいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
解の安定性の厳密な定義
厳密な定義を追記しておきます。
微分可能な関数\(f(x):\mathbb{R}^N \to \mathbb{R}^N\)によって定まる連立常微分方程式系\(\frac{dx}{dt}=f(x)\)を考えます。
\(\bar{x}\in \mathbb{R}^N\)が平衡解(equilibrium solution)、あるいは不動点(fixed point)とは、\(f(\bar{x})=0\)を満たすこと。
\(\bar{x}\)がリヤプノフ安定(Lyapunov stable)、(あるいは単に)安定とは、任意の\(\varepsilon >0\)に対し、次のような\(\delta >0\)が存在すること。「方程式の任意の解\(y(t)\)が、\( \| y(0) – \bar{x} \|< \delta \)を満たすならば、任意の\(t>0\)に対し\( \| y(t) – \bar{x} \|< \varepsilon \)を満たす」。
\(\bar{x}\)が不安定(unstable)とは、(リヤプノフ)安定ではないこと。
\(\bar{x}\)が漸近安定(asymptotically stable)とは、次のような\(\delta >0\)が存在すること。「方程式の任意の解\(y(t)\)が、\( \| y(0) – \bar{x} \|< \delta \)を満たすならば、\( \lim _{t \to \infty}\| y(t) – \bar{x} \|=0 \)を満たす」。
上記の定義では、\(\bar{x}\)の付近(\(\delta\)-近傍)の解のみを考えているため、局所安定(locally stable)、局所漸近安定(locally asymptotically stable)とも言えます。
もし\(\delta >0\)を限りなく大きく定めることができるなら、つまり無条件な解\(y\)に対して安定性が言えるならば、大域安定(globally stable)、大域漸近安定(globally asymptotically stable)と言います。
大域安定ならば局所安定ですが、逆は一般に正しいとは限りません。
線形な方程式では、局所安定性と大域安定性は一致します。
そして、非線形な方程式ではそうとは限らず、いくつかの不動点のまわりで局所的な安定性を議論することになります。
そのため、普通は局所安定性のことを単に安定性と呼ぶわけです。
シュプリンガー・フェアラーク東京
売り上げランキング: 1,154,556
朝倉書店
売り上げランキング: 372,923
こちらもおすすめ
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ
カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に