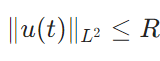どうも、木村(@kimu3_slime)です。
今回は、反応拡散方程式の力学系でアトラクターが存在することの証明を紹介します。
\(\Omega \subset \mathbb{R}^N\)をなめらかな有界領域とし、
\[\frac{\partial u}{\partial t} -\Delta u =f(u)\]
\[u(t,x)=0\quad(x\in \partial \Omega)\]
\[u(0,x)=u_0(x)\]
ただし\(f(s)=s-s^3\)といった反応拡散方程式を考えると、
- 「\(u_0 \in L^2\)に対し、「\(t \geq t_0\)ならば\(\|u(t)\|_{L^2} \leq R\)」を満たす\(t_0\)が存在する」ような\(R\)が存在する
- \(L^2\)の有界な吸収集合が存在する。
- 「\(u_0 \in L^2\)に対し、「\(t \geq t_0\)ならば\(\int_{t}^{t+1} \|u(s)\|_{H_0 ^1}^2 ds \leq R_1\)」を満たす\(t_0\)が存在する」を満たす\(R_1\)が存在する
ことを前回の記事で示しました。
今回は、\(H_0^1\)における有界な吸収集合が存在することを示し、それによって\(L^2\)におけるアトラクターが存在することを示します。
まず、解になめらかさがある、\(u \)が空間について2階微分可能として、方程式に\(-\Delta u\)をかけて空間について積分しましょう。
\[\int \frac{\partial u}{\partial t}(-\Delta u)dx +\int(-\Delta u)^2 dx =\int (u-u^3)(-\Delta u) dx\]
で、左辺は部分積分によって
\[\begin{aligned} &\int_{\Omega} \frac{\partial u}{\partial t}(-\Delta u)dx +\int_{\Omega}(-\Delta u)^2 dx \\ &= \sum_{k=1}^N \int_{\Omega} \frac{\partial^2 u}{\partial t \partial x_k} \frac{\partial u}{\partial x_k} dx+\|-\Delta u\|_{L^2}^2\\ &= \frac{1}{2}\frac{d}{dt}\|u\|_{H_0^1}^2 +\|-\Delta u\|_{L^2}^2\end{aligned}\]
となります。一方、右辺を\(f^{\prime}(s)=1-s^2 \leq 1 \)に注意して不等式評価すれば、
\[\begin{aligned} &\int_{\Omega} (u-u^3)(-\Delta u) dx \\ &= -\int_{\Omega}\sum_{k=1}^N (u-u^3) \frac{\partial^2 u}{\partial x_k^2}dx \\&= \int_{\Omega}\sum_{k=1}^N (1-u^2) \frac{\partial u}{\partial x_k} \frac{\partial u}{\partial x_k}dx \\ &\leq \int_{\Omega}\sum_{k=1}^N \frac{\partial u}{\partial x_k} \frac{\partial u}{\partial x_k}dx \\ &= \|\nabla u\|_{L^2}^2 \\&= \|u\|_{H_0 ^1}^2\end{aligned}\]
です。つまり、
\[\begin{aligned} &\frac{d}{dt}\|u\|_{H_0^1}^2 \\ &\leq 2 \|u\|_{H_0 ^1} -2\|-\Delta u\|_{L^2}^2 \\ &\leq 2\|u\|_{H_0 ^1}^2 \end{aligned}\]
です。
これを少し工夫して不等式評価します。\(t\)を実数とし、\(a\)を\(t-1 \leq a <t\)を満たす数とします。さきほどの不等式を、\(a\)から\(t\)まで時間について積分すれば、
\[\begin{aligned} &\|u(t)\|_{H_0^1}^2 \\ &\leq 2\int_{a}^t \|u(s)\|_{H_0^1}^2 ds+\|u(a)\|_{H_0^1}^2 \\ &\leq 2\int_{t-1}^t \|u(s)\|_{H_0^1}^2 ds+\|u(a)\|_{H_0^1}^2 \end{aligned}\]
です。さらに\(a\)について\(t-1\)から\(t\)まで積分すれば、
\[\begin{aligned} & \|u(t)\|_{H_0^1}^2\\ &\leq 2 \int_{t-1}^t \|u(s)\|_{H_0^1}^2 ds +\int_{t-1}^t\|u(a)\|_{H_0^1}^2da \\ &=3 \int_{t-1}^t \|u(s)\|_{H_0^1}^2 ds \end{aligned}\]
です。ここで\(L^2\)に関する評価
- 「\(u_0 \in L^2\)に対し、「\(t \geq t_0\)ならば\(\int_{t}^{t+1} \|u(s)\|_{H_0 ^1}^2 ds \leq R_1\)」を満たす\(t_0\)が存在する」を満たす\(R_1\)が存在する
を用いましょう。\(t_1 :=t_0+1\)とすれば、\(t \geq t_1\)のとき、\(t-1\geq t_0\)なので評価が使えます。したがって、
\[\begin{aligned} & \|u(t)\|_{H_0^1}^2\\ &\leq 3 \int_{t-1}^t \|u(s)\|_{H_0^1}^2 ds \\ & \leq 3R_1\end{aligned}\]
です。\(R_2 := \sqrt{3R_1}\)と置けば、それは\(u_0\)によらず、\(t \geq t_1\)のとき
\[\begin{aligned} \|u(t)\|_{H_0^1} \leq R_2\end{aligned}\]
となりました。
\(u\)になめらかさを仮定しましたが、一般のケースでも(ガラーキン)近似をすることによって同じ評価を導けます。詳しくはロビンソン「Infinite-Dimensional Dynamical Systems」を参照。
以上によって、\(H_0^1\)に有界な吸収集合が存在することが示せました。
\(\Omega\)は有界なので、ポアンカレの不等式から\(H_0^1\)と\(H^1\)のノルムは同値なので、\(H^1\)における有界な吸収集合\(B\)が存在します。
さらに、レリッヒ・コンドラショフの定理より、\(H^1\)における有界な集合は\(L^2\)におけるコンパクト集合なので、\(B\)は\(L^2\)において吸収集合です。
よって、\(L^2\)においてコンパクトな吸収集合が存在することが示せました。これにより反応拡散方程式の力学系は散逸系で、グローバルアトラクターが存在することが示せました。
以上、反応拡散方程式の力学系でアトラクターが存在することの証明を紹介してきました。
方程式の解の存在と一意性を調べることで解の長期挙動:力学系の議論を始めることができ、解のノルムの不等式評価によって吸収集合やアトラクターの存在を示すことができました。偏微分方程式の力学系の例として、今回の反応拡散方程式の話を知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
反応拡散方程式の力学系でL^2の吸収集合が存在することの証明