どうも、木村(@kimu3_slime)です。
今回は、棒グラフの読み取りと比較の問題を通して、全体の数に注意しようという話を紹介します。
ある小学校で、「進んであいさつをする」という目標を掲げ、それについて2学年ごとにアンケート調査をしました。
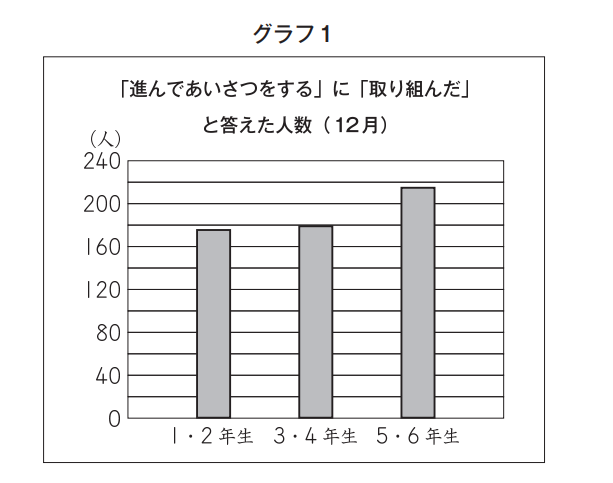
「取り組んだ」と答えた人数は、5・6年生が最も多いです。
また、1・2年生、3・4年生、5・6年生の学年の人数は、それぞれ175人、200人、250人と異なります。
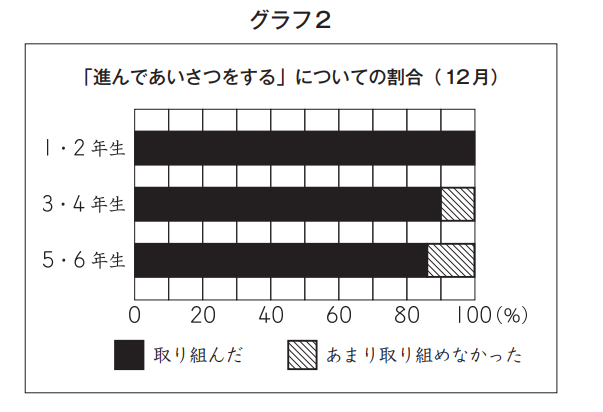
そこで、1・2年生、3・4年生、5・6年生それぞれの学年の人数を基準にしたときの「進んであいさつをする」に「取り組んだ」人数の割合を求め、グラフにしました。
2つのグラフを見て、結果のまとめとして正しい選択肢を選びましょう。
- 「進んであいさつをする」に「取り組んだ」と答えた人数が、最も少ないのは「ア」です。
- 「ア」の、「進んで挨拶をする」に「取り組んだ」と答えた人数の割合は、一番「イ」です。
アの選択肢
- 1・2年生
- 3・4年生
- 5・6年生
イの選択肢
- 小さい
- 大きい
画像引用:平成30年度 全国学力・学習状況調査
この問題は、平成30年度全国学力・学習状況調査、小学校算数Bの問題3(2)です。正答率は24.0%と低めです。
では、解説していきましょう。
まず、「進んであいさつをする」に「取り組んだ」と答えた人数が、最も少ないのはどのグループでしょうか。
おそらくよくある間違いが、選択肢の近くに書かれたグラフ2を見て、「5・6年生の取り組んだ割合が一番小さいから、答えはそれだ」というものではないでしょうか。
棒グラフなど割合の比較をするときに注意しなければならないことが、まさにこれです。つまり、割合が小さいからといって、その数が少ないとは限らないのです。これはグループ全体の人数(基準、もとになる数)が異なるときに起こりえます。
全体の数と割合から、何人が「取り組んだ」と答えたかを計算してみましょう。
| 全体(人) | 割合(%) | 「取り組んだ」(人) | |
| 1・2年生 | 175 | 100 | |
| 3・4年生 | 200 | 90 | |
| 5・6年生 | 250 | 80~90の間 |
「取り組んだ人数」は、どうやって求められるでしょうか。それは全体に割合をかけたものです。割合は%、百分率で表されているので、例えば\(90\)をそのままかけるのではなく、\(\frac{90}{100}=0.9\)であることに注意しましょう。
| 全体(人) | 割合(%) | 「取り組んだ」(人) | |
| 1・2年生 | 175 | 100 | 175 |
| 3・4年生 | 200 | 90 | 180 |
| 5・6年生 | 250 | 80~90の間 | 200~225の間 |
5・6年生の「取り組んだ」割合は、グラフ2からは正確には読み取れません。しかし、少なくとも80%よりは多いです。したがって、少なくとも200人よりは多いとわかります。比較にはこれで十分です。
この計算結果を読み取れば、
- 「進んであいさつをする」に「取り組んだ」と答えた人数が、最も少ないのは「ア 1・2年生」です。
- 「ア 1・2年生」の、「進んで挨拶をする」に「取り組んだ」と答えた人数の割合は、一番「イ 大きい」です。
と答えられますね。最も割合の大きなグループが、最も人数が少ないのです。グループごとに基準とする人数が異なるので、割合の大小と人数の大小が一致するとは限らないことに注意しましょう。
アンケート調査やニュースにおいて、割合を示した棒グラフはよく利用されています。
- 割合を提示されたら、全体(母集団)が何人かに注目する
ようにしましょう。割合とは、全体と一部分の比較をしたものです。全体が10人か、100人か、10000人かによって、同じ割合10%割合でも、その意味=一部分の人数は、1人、10人、1000人と変わります。
以上、棒グラフの読み取りと比較の問題を通して、全体に注意しようを紹介してきました。
全体の数を意識せずに、割合だけを単純に比較すると誤った理解をしてしまうかもしれません。割合とは比較をする数なので、何を基準として何を一部分としているかを意識しましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)
こちらもおすすめ
混み具合(人口密度)の計算では単位の意識を:シートの面積と人数の問題を例に