座標を使った中点の求め方、公式の証明

どうも、木村（@kimu3_slime）です。

今回は、座標を使った中点公式の証明を紹介します。

例えば、\(A=(1,1)\)と\(B= (-1,1)\)の中点は、それぞれの成分を足して2で割ったもの、\(M=(\frac{1-1}{2},\frac{1+1}{2})=(0,1)\)として求められます。

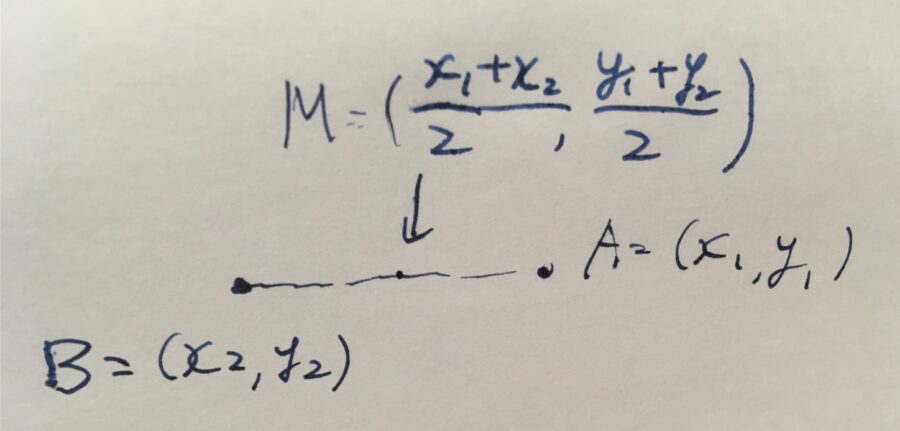
一般に2つの点を直交座標で\(A=(x_1,y_1)\)、\(B=(x_2,y_2)\)と表すとき、中点\(M\)は

\[M = (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\]

となります。\(x\)座標、\(y\)座標それぞれの平均が中点となるわけです。

では、\(M\)が線分\(AB\)の中点であることを証明しましょう。

中点であるとは、

\(M\)が線分\(AB\)上にあって
\(A\)から\(M\)への距離と、\(B\)から\(M\)への距離が等しい

ことです。

まず、\(M=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})\)が\(A,B\)によって定まる直線上にあること、3つの点が共線的であることを示しましょう。

\(A\)を基準とした幾何ベクトルを考えると、\(AB=B-A = (x_2-x_1,y_2-y_1) \)、\(AM=M-A= (\frac{x_2-x_1}{2},\frac{y_2-y_1}{2})\)と表せます。したがって、\(AB = \frac{1}{2}AM\)となるので、\(A,B,M\)は同一直線上にあり（\(AB,AM\)は線形独立でない）、\(M\)が線分\(AB\)上の点であることが示せました。

続いて、距離が等しいことを示しましょう。一般に、2点\(A,B\)の（ユークリッド）距離\(d(A,B)\)は

\[d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]

です。この一方を中点\(M\)に置き換えて計算すると、\((x_1-x_2)^2=(x_2-x_1)^2\)であることに注意して、

\[d(A,M)=\sqrt{(x_1-(\frac{x_1+x_2}{2}))^2+(y_1-\frac{y_1+y_2}{2})^2} \\ \sqrt{(\frac{x_2-x_1}{2})^2+(\frac{y_2-y_1}{2})^2}\]

\[d(B,M)=\sqrt{(x_2-(\frac{x_1+x_2}{2}))^2+(y_2-\frac{y_1+y_2}{2})^2} \\ \sqrt{(\frac{x_2-x_1}{2})^2+(\frac{y_2-y_1}{2})^2}\]

となるので、\(d(A,M)=d(B,M)\)となることが示せました。よって、\(M\)は\(A,B\)の中点です。

今回は2次元で証明しましたが、一般の次元、\(N\)次元でも同様です。\(A=(a_1,\dots,a_N)\)、\(B=(b_1,\dots,b_N)\)の中点は、

\[M = (\frac{a_1+b_1}{2},\dots, \frac{a_N+b_N}{2})\]

となります。

以上、座標を使った中点公式の証明を紹介してきました。

足して二等分するという結果は簡単なので覚えやすいかと思いますが、「中点であるとはどういうことか」を理解するとより納得しやすいでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。