平行四辺形の面積の求め方の証明

どうも、木村（@kimu3_slime）です。

今回は、平行四辺形の面積の求め方の証明を紹介します。

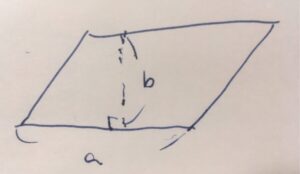
平行四辺形の面積は、一辺の長さを\(a\)、それを基準とした高さを\(b\)とするとき、\(ab\)となります。

長方形の面積がそれぞれの辺の長さの積\(ab\)になることを議論の出発点として、平行四辺形の面積の求め方を証明しましょう。

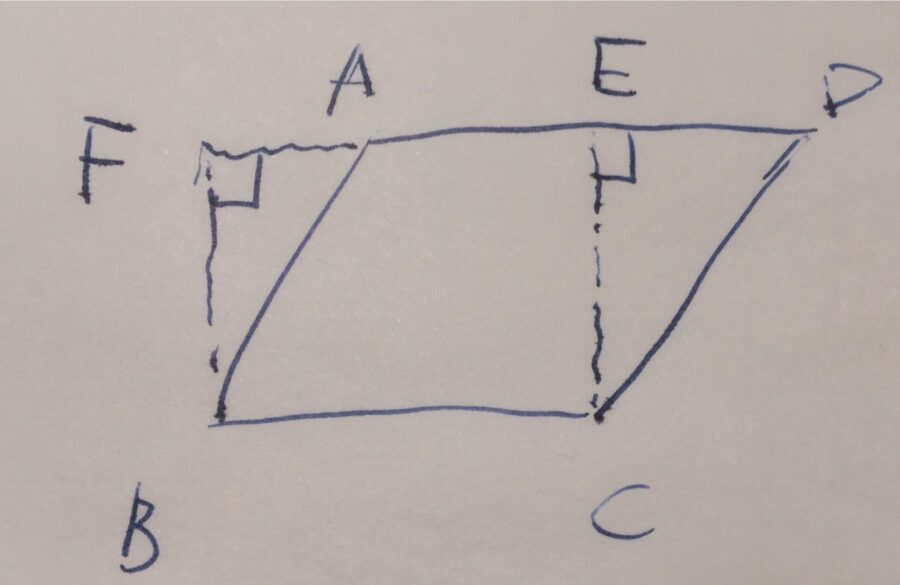
平行四辺形を\(ABCD\)とします。\(AD\)を延長した直線を引き、それに対し\(C,B\)を通る垂線を引き、交わる点を\(E,F\)としましょう。

このとき、\(ABCD\)の面積は、三角形部分を動かした\(FBCE\)に等しいことを示しましょう。

面積の原則（公準）として、

があります。したがって、\(\triangle CED,\triangle BFA\)が合同となることが示せれば、

\[\begin{aligned} & (ABCDの面積)\\ &=(ABCEの面積)+ (CEDの面積)\\&=(ABCEの面積)+ (BFAの面積)\\&= (FBCDの面積)\end{aligned}\]

となることが示せます。

まず、垂線と交わる点として\(E,F\)を定めたので、\(\angle CED=\angle BFA=90^{\circ}\)です。また、\(BC,AD\)は平行四辺形の向かい合う辺なので平行です。平行な直線の距離、垂線の長さは一定なので、\(CE=BF\)となります。また、平行四辺形の向かい合う辺の長さは等しいので、\(CD=BA\)です。

まとめれば、平行四辺形\(ABCD\)の面積は、長方形\(FBCE\)の面積に等しいです。長方形の面積は直交する2つの辺の長さの積に等しいので、平行四辺形の面積が一辺と高さの積\(ab\)に等しいことが示せました。

以上、平行四辺形の面積の求め方の証明を紹介してきました。

三角形部分を移動して長方形の面積に帰着させるというアイデアを知っておくだけでも計算に納得しやすくなるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。