どうも、木村(@kimu3_slime)です。
今回は、ピタゴラスの定理の逆、直角三角形となることの証明を紹介します。
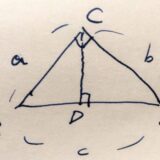
ピタゴラスの定理とは、直角三角形の辺の長さ\(a,b,c\)について、\(a^2+b^2=c^2\)が成り立つことでした。これは逆が成り立ちます。
どんな三角形であっても、辺の長さを\(a,b,c\)として、\(a^2+b^2=c^2\)が成り立つならば、その三角形は直角三角形となります。これがピタゴラスの定理の逆です。
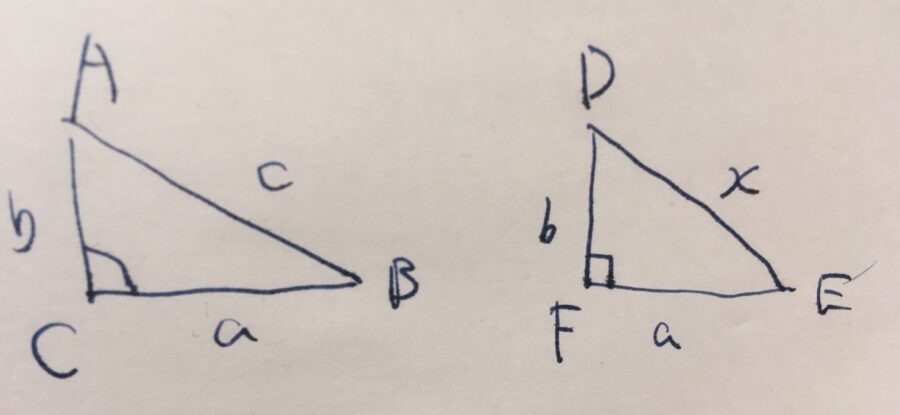
では、証明していきましょう。
まず、辺の長さを\(a,b,c\)とする三角形を\(\triangle ABC\)とします。示すべきことは、\(\angle ACB=90^{\circ}\)です。
別の三角形として、長さ\(a,b\)の辺を持ち、それらの辺が直交しているような直角三角形\(\triangle DEF\)を考えましょう。斜辺の長さはわからないので、\(x\)とします。
\(\triangle DEF\)は直角三角形とわかっているので、ピタゴラスの定理から、\(a^2+b^2= x^2\)が成り立ちます。また、仮定より\(a^2+b^2=c^2\)であったので、\(x^2=c^2\)です。辺の長さは正\(x,c>0\)なので、\(x=c\)となります。
よって、三角形の合同条件、3つの辺の長さが等しいならば合同なので(SSS)、\(\triangle ABC,\triangle DEF\)は合同です。
合同な三角形の対応する角度は等しいので、\(\angle ACB=\angle DFE=90^{\circ}\)であることが示せました。
以上、ピタゴラスの定理の逆の証明を紹介してきました。
「直角三角形ならば\(a^2+b^2=c^2\)」だけでなく、その等式が成り立つならば直角三角形である、という角度を決めるような等式ですね。これはピタゴラスの定理の一般化、(第二)余弦定理にも通じるような視点と言えます。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)