相似な三角形の高さが辺の長さに比例することの証明

どうも、木村（@kimu3_slime）です。

今回は、相似な三角形の高さが辺の長さに比例することの証明を紹介します。

相似な三角形\(\triangle ABC, \triangle DEF\)について考えましょう。\(BC,EF\)を基準とした高さを、\(AG,AH\)とします。

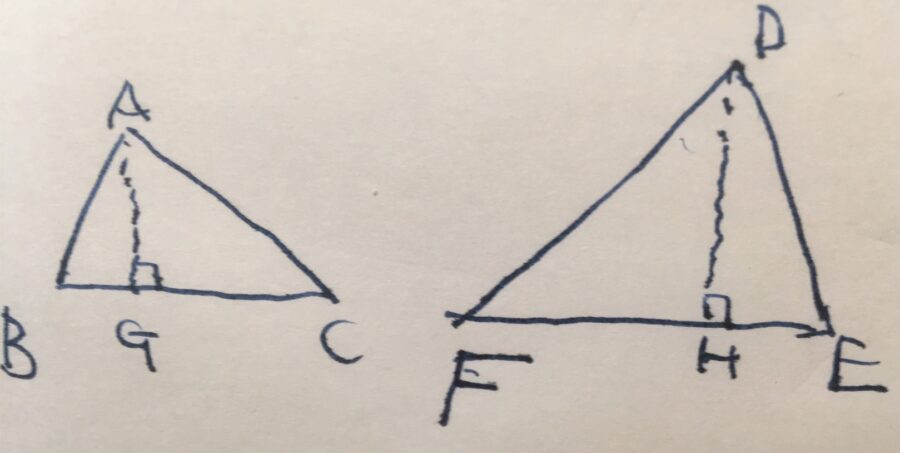
このとき、それらの高さは辺の長さに比例し、\(\frac{AG}{DH}=\frac{AB}{DE}\)となります。

ちなみに、ある辺を基準とした高さ（altitude）とは、その辺の垂線で、隣接しない頂点を通る線分の長さのことです。

では、証明していきましょう。垂線によってできる三角形が相似になることを示します。

\(\triangle ABG,\triangle DEH\)に注目します。

\(\triangle ABC, \triangle DEF\)が相似で、対応する角度は等しいことから、\(\angle ABG=\angle DEH\)です。また、\(AG,BH\)は\(BC,EF\)の垂線であることから、\(\angle AGB =\angle DHE\)です。

よって、三角形の相似条件、2つの角度が等しいこと（AA）から、\(\triangle ABG,\triangle DEH\)は相似です。

相似な三角形の対応する辺の長さの比は一定なので、\(\frac{AG}{DH}=\frac{AB}{DE}\)が示せました。

以上、相似な三角形の高さが辺の長さに比例することの証明を紹介してきました。

図を描くと当たり前のように見えますが、相似の考え方を使って証明できるとすっきりしますね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ