どうも、木村(@kimu3_slime)です。
一般に、平行四辺形の向かい合う辺の長さは等しくなります。逆に、どんな条件を満たせば四角形は平行四辺形となるのでしょうか?
今回は、平行で長さの等しい2つの辺を持つ四角形は平行四辺形であることの証明を紹介します。
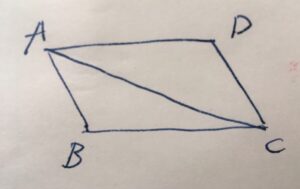
四角形\(ABCD\)があり、長さが等しく平行な2つの辺があるとします。例えば、\(AB =CD\)で、\(AB,CD\)は平行とします。
このとき、\(ABCD\)は平行四辺形になります。つまり、\(BC,DA\)も平行となることが証明できます。
証明していきましょう。
対角線\(AC\)を引き(定規公準)、それによってできる三角形\(\triangle ABC, \triangle CDA\)に注目します。
2つの線分\(BC,DA\)が平行であることを示すには、その錯角\(\angle ACB ,\angle CAD\)の大きさが等しいことを示せば良いです。
まず、仮定より\(AB =CD\)です。また、\(AB ,CD\)は平行で、一般に錯角の大きさは等しいので、\(\angle BAC = \angle DCA\)です。さらに、共通する辺として、\(AC=CA\)です。
よって、三角形の合同条件、2つの辺の長さとその間の角度が等しいので(SAS)、\(\triangle ABC, \triangle CDA\)は合同です。
特に、対応する角度は等しいので、\(\angle ACB =\angle CAD\)です。以上によって、錯角の大きさが等しいので、\(BC,DA\)が平行であることが示せました。つまり、\(ABCD\)は平行四辺形です。
以上、平行で長さの等しい2つの辺を持つ四角形は平行四辺形であることの証明を紹介してきました。
これは三角形の中点連結定理の証明において、平行四辺形ができることの証明に使えます。
「向かい合う辺が平行」が平行四辺形の定義ですが、別の部分的な情報からも平行四辺形であると判定できることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)