三角形の中点連結定理の証明

どうも、木村（@kimu3_slime）です。

今回は、三角形の中点連結定理の証明を紹介します。

\(\triangle ABC\)を考え、2つの辺\(AB,AC\)の中点を\(M,N\)とします。つまり、\(AM=BM,AN=CN\)とします。

このとき、中点同士をつなぐ線分\(MN\)の長さはもうひとつの辺\(BC\)の長さの半分である\(MN= \frac{1}{2}BC\)であり、さらに\(MN,BC\)は平行となります。これが中点連結定理（midpoint theorem）と呼ばれる性質です。

証明していきましょう。方針は補助線を引き、合同な三角形、平行四辺形を見出すことです。

まず、\(B\)を通り\(AC\)に平行な直線を引きましょう（平行線公準）。その直線と\(MN\)を延長した直線の交点を\(D\)、平行線上の\(D\)から見て\(B\)側でない点を\(E\)とします。

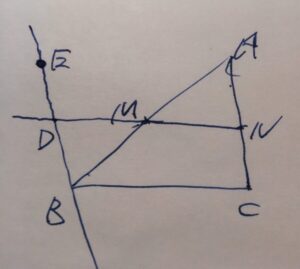
\(\triangle AMN, \triangle BMD\)が合同であることを示しましょう。

\(M\)は\(AB\)の中点であることから、\(AM =BM\)です。\(M\)は2つの直線の交点であり、一般に対頂角は等しいので、\(\angle AMN = \angle BMD\)です。

さらに、\(AN,BN\)は平行であり、平行線の錯角は等しいです。したがって、\(\angle MAN =\angle MBD\)となります。

よって、三角形の合同条件、1辺の長さとその両端の角度が等しい（ASA）から、\(\triangle AMN, \triangle BMD\)は合同です。

特に、対応する辺の長さは等しいので、\(AN= DB\)です。さらに\(N\)は\(AC\)の中点なので、\(AN =NC\)です。したがって、\(NC, DB\)は平行で長さが等しくなります。

よって、\(BC,ND\)は平行で、特に\(BC,BM\)が平行であることがわかりました。

また、三角形の合同から\(MN= DM\)で、平行四辺形\(BCND\)の向かい合う辺の長さは等しいので\(DM+MN =BC\)です。これらを合わせれば、\(MN = \frac{1}{2}BC\)であることが示せました。

以上、三角形の中点連結定理の証明を紹介してきました。

長さについては三角形、平行については平行四辺形を見出すことで、中点をつないだ線分の性質が理解できますね。

木村すらいむ（@kimu3_slime）でした。ではでは。

posted with AmaQuick at 2022.05.16

()

￥13,970 (中古品)

こちらもおすすめ