合同な三角形の垂線の長さが等しいことの証明

どうも、木村（@kimu3_slime）です。

今回は、合同な三角形の垂線の長さが等しいことの証明を紹介します。

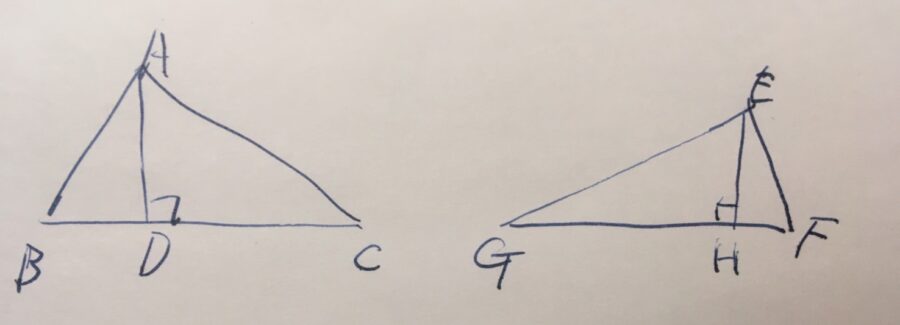
2つの合同な三角形、\(\triangle ABC\)と\(\triangle EFG\)があるとしましょう。対応する頂点からの垂線と辺の交点を、\(D,H\)とします。

このとき、必ず垂線の長さは等しい\(AD = EH\)です。

ちなみに、垂線（altitude）とは、ある頂点を通り、その反対側の辺に垂直な線分のことです。

では、証明していきましょう。端的に言えば、垂線によって合同な2つの三角形ができて、垂線はその対応する辺なので長さが等しい、という流れです。

\(AD,EH\)は垂線であることから、\(\angle ADB = 90^\circ\)、\(\angle EHF = 90^\circ\)です。つまり、\(\angle ADB =\angle EHF \)です。

また、\(\triangle ABC\)と\(\triangle EFG\)が合同であることから、\(AB=EF\)、\(\angle ABD = \angle EFH\)です。

三角形の内角の和は180度なので、\(\angle ADB+ \angle ABD+ \angle BAD=180^\circ\)、\(\angle EHF+ \angle EFH+ \angle FEH=180^\circ\)です。したがって、これまでの角度が等しい情報を用いれば、\(\angle BAD = \angle FEH\)となります。

よって、三角形の合同条件、1組の辺の長さとその両端の角度が等しい（AAS）ので、\(\triangle ABD\)と\(\triangle EFH\)は合同です。特に対応する辺の長さは等しく、\(AD = EH\)が示せました。

以上、合同な三角形の垂線の長さが等しいことの証明を紹介してきました。

図を書くと当たり前に見えるかもしれませんが、角度や合同条件を用いることできちんと証明できるのは嬉しいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。