傾きが等しい直線は交わらない（平行）ことの証明、平行の定義

どうも、木村（@kimu3_slime）です。

今回は、傾きが等しい直線は交わらない（平行）であることの証明、平行の定義について紹介します。

傾きと平行の関係
傾きが等しいとき交わらない証明
平行の定義
こちらもおすすめ

傾きと平行の関係

例として、次の図のような直線\(\ell , m\)を考えましょう。

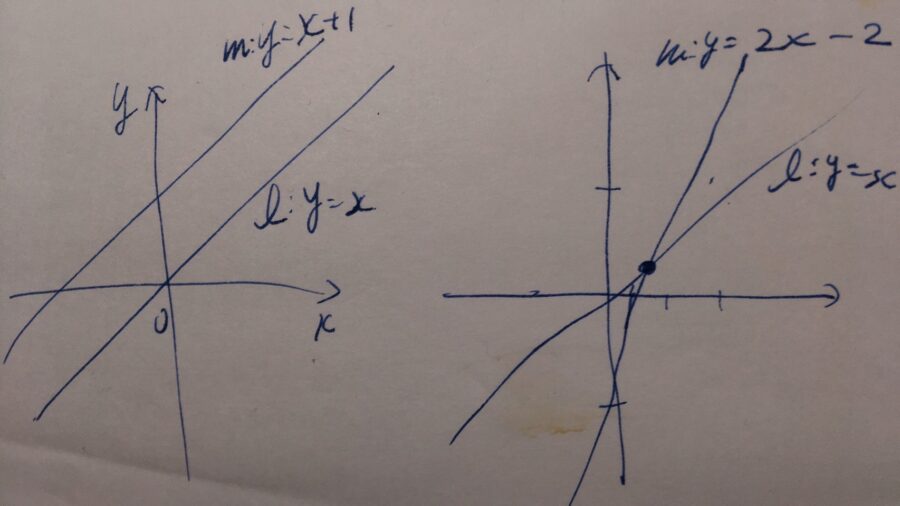
平面上の直線は、座標を用いることによって、\(y=ax+b\)という形で表せます。そして、係数\(a\)を直線の傾きと呼びます。

図の左側において、\(\ell\)の傾きは1、\(m\)の傾きは1と等しいです。これらの直線は、交わりません。交わらない直線のことを、平行であると呼びます。

もし交わる点\((x,y)\)があるならば、\(y\)座標が等しく、\(x = x+1\)が成りたちます。しかし、それは\(0=1\)を満たします。これは矛盾なので、そのような点\((x,y)\)は存在しない、つまり交わらないということです。

一方で、図の右側において、\(\ell\)の傾きは2、\(m\)の傾きは1と等しくありません。これらの直線は、交わる点を持ちます。

実際、\(x = 2x-2\)を満たす点は存在します。\(x=2\)かつ\(y=2\)となる点\((2,2)\)ですね。

傾きが等しいとき交わらない証明

ここまでの議論を一般化しましょう。

直線\(y= a_1 x +b_1\)と直線\(y = a_2 x+b_2\)について考えます。

これらの直線は、傾きが等しく\(a_1 =a_2\)、かつ完全に重ならない（\(b_1 \neq b_2\)）のとき、交わる点を持ちません（平行です）。

もし交わる点があったとすると、\(a_1 x +b_1 = a_1 x +b_2\)が成りたちます。したがって、\(b_1 =b_2\)が導かれますが、これは仮定に反します。よって、交わる点を持たないことが示せました。

（ちなみに、\(b_1=b_2\)のときは、直線は完全に重なり、直線上のすべての点で交わっていると言えます。）

また、2つの直線は、傾きが異なる\(a_1 \neq a_2\)とき、交わる点を持ちます（平行でない）。

交わる点は\(a_1 x +b_1 = a_2 x+b_2\)を満たします。\(a_1 \neq a_2\)であることに注意して、\(a_1 -a_2\)で割れば、\(x = \frac{b_2-b_1}{a_1 -a_2}\)です。対応する\(y\)座標は、\(a_1 \frac{b_2 -b_1}{a_1-a_2}+b_1\)ですね。よって、交わる点が存在することが示せました。

平行の定義

2つの直線が平行であることの定義は、いくつかの種類が知られています。

交わらない
第3の直線と同じ角度で交わる（傾きが等しい）
等距離である（一定の距離を保つ）

さきほどは、直線の傾きが等しいことと、交わらないことが同値であることを示しました。傾きが等しいなら交わらないし、傾きが等しくないなら交わります（対偶を考えれば、交わらないならば傾きは等しくない）。

傾きが等しいとは、第3の直線と同じ角度で交わることと（平行線公理を用いれば）言い換えられます。例えば、傾きが1の直線は、\(x\)軸という直線となす角度が\(45^{\circ}\)です。

さらに、傾きが等しいことは、等距離であることと同値であることも示せますね。確かめてみましょう。

\(a_1 =a_2\)のとき、2つの直線の\(y\)座標の差は、\((a_1x+b_1)-(a_1 x+b_2)= b_1 -b_2\)であり、\(x\)によらず一定となります。

\(a_1 \neq a_2\)のとき、2つの直線の\(y\)座標の差は、一定ではありません。\(x=0\)のときの差は\(d_1 =b_1 -b_2\)で、\(x=1\)のときの差は\(d_2 = a_1 -a_2 +b_1 -b_2= a_1-a_2 +d_1\)です。よって、これらの差は\(d_1 -d_2 = a_1 -a_2 \neq 0\)なので、一定ではないことが示せました。

以上、傾きが等しい直線は交わらない（平行）であることの証明、平行の定義について紹介してきました。

平面におけるよく知られた幾何学、ユークリッド幾何学では、