どうも、木村(@kimu3_slime)です。
今回は、弦の基本振動とは何か、三角関数と波動方程式による説明をします。
高校物理における基本振動
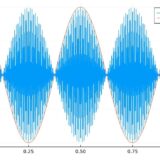
両端を固定した弦をはじくと、波の山が時間とともに上下する形で弦が振動します(定常波)。
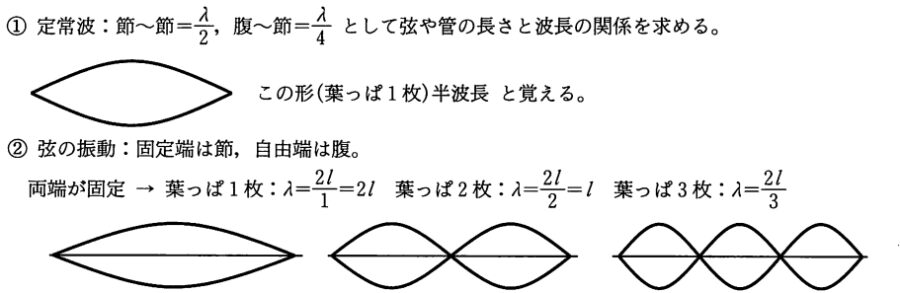
画像引用:実戦物理重要問題集 物理基礎・物理
山が1個の振動は基本振動と呼ばれます。山が2個ならば2倍振動、3個ならば3倍振動、n個ならばn倍振動です。
次の動画は、\(-\pi < x < \pi\)の区間での振動と考えれば、2倍振動です。
波動方程式による基本振動の説明
波動方程式の解は、三角関数の和
弦の振動現象は、波動方程式という偏微分方程式によって説明できることが知られています。
\(u(t,x)\)を時間\(t\)位置\(x\)における弦の変位とすると、
\[ \begin{aligned}\frac{\partial ^2 u}{\partial t^2} = \frac{\partial ^2 u}{\partial x^2}\end{aligned} \]
という方程式を満たします。
元の長さを\(\ell\)とし、区間\([0, \ell] =\{x \mid 0 \leq x \leq \ell\}\)における波動方程式を考えましょう。
固定端の振動を考えることは、境界条件を\(u(t,0)=u(t,\ell)= 0\)とすることに対応します。
この条件で波動方程式を解くと、
\[u_n(t,x) = \cos (\frac{n\pi }{\ell}t) \sin (\frac{n \pi }{\ell} x)\]
という三角関数の足し合わせが解となることが知られています。
複雑な音や振動は、実は単純な三角関数の足し合わせ(フーリエ級数)として捉えられるわけですね。
参考:1次元波動方程式の解き方:変数分離法、フーリエ級数展開
基本振動とn倍振動
実は、これらが基本振動、n倍振動を表す関数です。
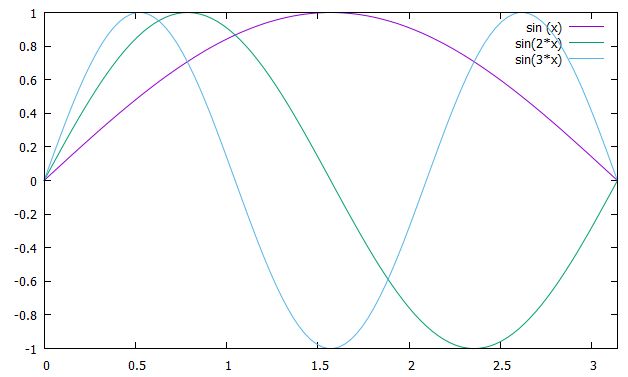
\(n=1\)のとき、
\[u_1(t,x) = \cos (\frac{\pi }{\ell}t) \sin (\frac{ \pi }{\ell} x)\]
を基本振動と呼びます。
\(x=0\)のとき、\(\sin\)の偏角は0なので、\(u_1(t,0)=0\)です。\(x=\ell\)のとき、\(\frac{ \pi }{\ell} \ell = \pi\)なので、\(u_1(t,\ell)=0\)です。確かに固定端の条件を満たした、山がひとつの振動となっていますね。
偏微分(特定の変数に関する微分)をすると、
\[ \begin{aligned} \frac{\partial u_1 }{\partial t } =\frac{\pi }{\ell} \cos (\frac{\pi }{\ell}t) \sin (\frac{ \pi }{\ell} x) \\ \frac{\partial^2 u_1 }{\partial t^2 }= – (\frac{\pi }{\ell})^2\sin (\frac{\pi }{\ell}t) \sin (\frac{ \pi }{\ell} x) \end{aligned} \]
\[ \begin{aligned} \frac{\partial u_1 }{\partial x } = \frac{\pi }{\ell}\sin (\frac{\pi }{\ell}t) \cos (\frac{ \pi }{\ell} x) \\ \frac{\partial^2 u_1 }{\partial x^2 }= – (\frac{\pi }{\ell})^2 \sin (\frac{\pi }{\ell}t) \sin (\frac{ \pi }{\ell} x) \end{aligned} \]
となるので、波動方程式
\[ \begin{aligned}\frac{\partial ^2 u_1}{\partial t^2} = \frac{\partial ^2 u_1}{\partial x^2}\end{aligned} \]
を確かに満たしています。
\[u_n(t,x) = \cos (\frac{n\pi }{\ell}t) \sin (\frac{n \pi }{\ell} x)\]
が\(n\)倍振動を表す解です。
基本振動と同様にして、波動方程式を満たすことが確かめられます。
基本振動、n倍振動はあわせて、固有振動と呼ばれるものです。
波長と弦の長さの関係
基本振動
\[u_1(t,x) = \cos (\frac{\pi }{\ell}t) \sin (\frac{ \pi }{\ell} x)\]
の波長を\(\lambda_1\)とします。弦の長さ\(\ell\)との関係を調べてみましょう。
波長とは三角関数1周期の空間的な長さなので、\(\frac{ \pi }{\ell} \lambda_1 =2 \pi\)を満たします。したがって、\(\lambda_1 = 2 \ell\)です。
\(n\)倍振動
\[u_n(t,x) = \cos (\frac{n\pi }{\ell}t) \sin (\frac{n \pi }{\ell} x)\]
の波長\(\lambda_n\)を求めてみましょう。
同様に、\(\frac{n \pi }{\ell} \lambda_n =2 \pi\)を満たすので、\(\lambda_n = \frac{2}{n} \ell\)です。
固有振動の振動数\(f_n\)について考えましょう。これらは固有振動数と呼ばれています。
振動数は波長の逆数なので、
\[f_1 = \frac{1}{\lambda_1} = \frac{1}{2 \ell}\]
\[f_n = \frac{1}{\lambda_n} = \frac{n}{2 \ell}\]
となり、
\[f_n = n f_1\]
となっています。n倍振動の振動数は基本振動のn倍である、これが基本振動やn倍振動という名前の由来ですね。
以上、弦の基本振動とは何か、三角関数と波動方程式による説明をしてきました。
波動方程式の話は難しかったかもしれませんが、弦の振動や基本振動について考えるときに、三角関数の性質を用いていることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥1,990 (コレクター商品)