うなりの原理、回数の理由：三角関数による証明

どうも、木村（@kimu3_slime）です。

高校物理では、周波数（振動数）\(f_1,f_2\)の音波があり、それらが近いとき、うなりと呼ばれる干渉が起こることを学びます。

そして、1秒間あたりのうなりの回数は\(|f_1-f_2|\)となると説明されます。

この理由を、三角関数によって説明しましょう。

2つの物体が振動する現象は、振動する物体に周期的な外力が加わる現象、強制振動として捉えられます。

つまり、2つの物体の振動の角周波数を\(\omega_1 ,\omega_2\)とするとき、振動を表す関数\(x(t)\)は次の微分方程式を満たします。

\[ \begin{aligned}\frac{dx^2}{dt^2}+\omega _1 ^2 x = F \cos \omega_2 t\end{aligned} \]

この方程式の一般解は、次の通りです。

\[ \begin{aligned}x(t) =C_1 \cos \omega_1 t +C_2 \sin \omega_1 t\\+ \frac{F}{ \omega_1 ^2 -\omega_2 ^2} \cos \omega_2 t \end{aligned} \]

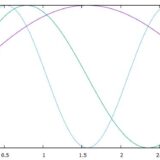
この解を調べることによって、うなりの回数を求めます。単純化のため、係数がシンプルになるケース（音の大きさが等しいケース）を考えましょう。

\[ \begin{aligned}x(t) = \cos \omega_1 t +\cos \omega_2 t \end{aligned} \]

三角関数の加法定理、和積の公式

\[\cos A +\cos B = 2 \cos \frac{A+B}{2} \cos \frac{A-B}{2}\]

を用いると、

\[ \begin{aligned}x(t) &= 2 \cos (\frac{\omega _1+\omega_2}{2}t) \cos (\frac{\omega _1-\omega_2}{2}t) \\ &= 2 \cos ( \frac{f_1+f_2}{2} 2\pi t) \cos (\frac{f _1 – f_2}{2}2\pi t)\end{aligned} \]

となります。ここで各周波数と周波数の関係\(\omega = 2 \pi f\)を用いました。

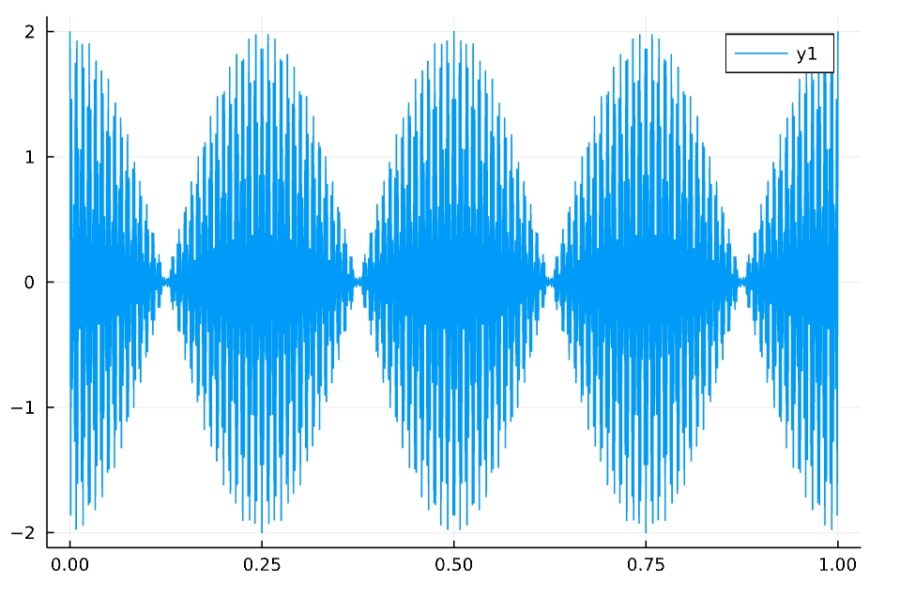
この式がうなりの原理の説明です。

\(f_1,f_2\)が近いとき、\(\frac{f _1 – f_2}{2}\)は小さくなるので、\(\cos (\frac{f _1 – f_2}{2}2\pi t)\)の音は極めて低く、聞き取りにくい音になります。\(\frac{f_1+f_2}{2}\)は平均なので、音の高さはほぼ変化せず、\(\cos ( \frac{f_1+f_2}{2} 2\pi t) \)の項が聞こえます。

ただし、音の強弱が目立つようになります。\(\cos (\frac{f _1 – f_2}{2}2\pi t)\)の周期は、\(T=\frac{2\pi}{\frac{|f _1 – f_2|}{2}2\pi}= \frac{2}{|f_1-f_2|}\)です。分母小さいので、これは人間でも聞き取れる周期となります。

三角関数には1周期あたり2回のピークがあるので、1秒あたりのうなりの回数（周波数）は、\(\frac{1}{T}\frac{1}{2} = |f_1-f_2|\)と求めることができました。

以上、うなりの回数の理由と原理について、三角関数による証明を紹介してきました。

微分方程式の議論をのぞけば、三角関数の加法定理を用いて理解できる話です。うなりとはどういう現象なのか、数式で理解するために役に立てば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。