平面波の干渉の性質を三角関数を用いて証明

どうも、木村（@kimu3_slime）です。

今回は、平面波の干渉の性質を三角関数を用いて証明します。

高校の物理学では、次のような図で波の干渉が説明されます。

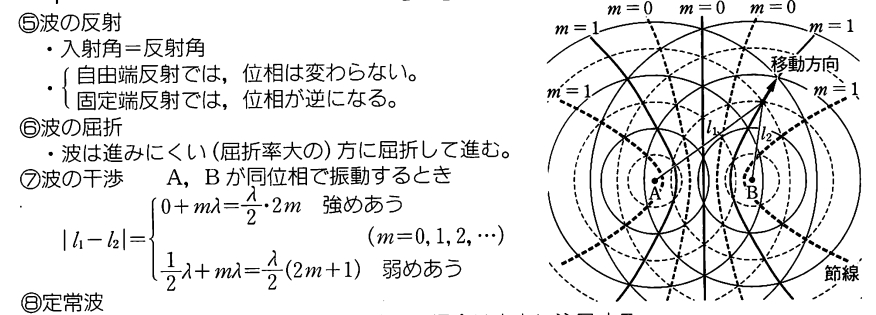
同位相で振動する波源\(A,B\)によって、平面波が発生している状況を考えます。\(A\)からの距離が\(\ell _1\)、\(B\)からの距離が\(\ell _2\)となる点に注目しましょう。その点で波が干渉するか、次の条件で決まります。

\[|\ell_1 -\ell_2|= \begin{cases}m \lambda & 強めあう\\ \frac{1}{2}\lambda +m\lambda & 弱めあう\end{cases}\]

\(\lambda\)は波の波長、\(m\)は整数です。波源からの距離の差が、波長の整数倍ならば強めあい、波長の整数倍から波長の半分だけずれるならば弱めあう、という主張となります。

では、この性質を証明していきましょう。

波の性質は、理論的には波動方程式によって説明されます。

今回考えているのは、\(u(x,t)= A\sin (x-t)\)のような空間的に広がっていく波、進行波です。

\(u(x,t)= \sin (x-t)\)という式は、空間変数\(x\)が1次元です。平面の進行波は、波源からどの方向にも同じように伝わるため、同じ形の式で表せます。つまり、波源からの距離が\(\ell_1\)ならば、\(u(\ell_1 ,t) = \sin (\ell_1 -t)\)といった形です。

波には振幅\(A\)、波長（空間的な周期）\(\lambda\)と、時間的な周期\(T\)があります。今回は、それらが等しい状況を考えています。すると、2つの波は

\[u_1(\ell_1 ,t) =A \sin (2\pi (\frac{\ell_1}{\lambda} – \frac{t}{T}))\]

\[u_2(\ell_2 ,t) =A \sin (2\pi (\frac{\ell_2}{\lambda} – \frac{t}{T}))\]

と表せるわけです。

波には重ね合わせの原理があるので、2つの波源からの波を合わせた波\(U\)は

\[\begin{aligned} U(x,y,t)&= u_1(\ell_1 ,t)+u_2(\ell ,t)\\&=A \sin (2\pi (\frac{\ell_1}{\lambda} – \frac{t}{T}))+A \sin (2\pi (\frac{\ell_2}{\lambda} – \frac{t}{T})) \end{aligned}\]

となります。

これを変形していきましょう。三角関数の加法定理

\[\sin \alpha +\sin \beta = 2 \cos (\frac{\alpha -\beta}{2}) \sin (\frac{\alpha +\beta}{2})\]

より、

\[U = 2A \cos (\frac{\pi}{\lambda}(\ell_1 -\ell_2)) \sin(\pi(\frac{\ell_1+\ell_2}{\lambda}-\frac{2t}{T}))\]

後半の\(\sin \)の部分は時間変化しますが、前半の\(\cos\)の部分は時間変化せず、波長と\(\ell_1,\ell_2\)によってのみ決まっています。

振幅を評価すると、コサインの性質から

\[|\cos (\frac{\pi}{\lambda}(\ell_1 -\ell_2))|= \begin{cases}1 & (|\ell_1 -\ell_2|=m \lambda )\\0 & (|\ell_1 -\ell_2| = \frac{\lambda}{2}+m\lambda)\end{cases}\]

となります。前者が干渉によって強めあう点、後者が弱めあう点なので、

\[|\ell_1 -\ell_2|= \begin{cases}m \lambda & 強めあう\\ \frac{1}{2}\lambda +m\lambda & 弱めあう\end{cases}\]

という性質を導くことができました。

以上、平面波の干渉の性質を三角関数を用いて証明してきました。

重ね合わせの原理と三角関数を知っていれば理解できる話なので、知っておくと干渉の性質が納得しやすいでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。