どうも、木村(@kimu3_slime)です。
今回は、理論分布(正規分布)の当てはめの適合度検定について、Juliaによる計算例を紹介します。
理論分布への当てはめの適合度検定
あるテストを100人に受けてもらったところ、そのヒストグラムは次のようになっていたとしましょう。
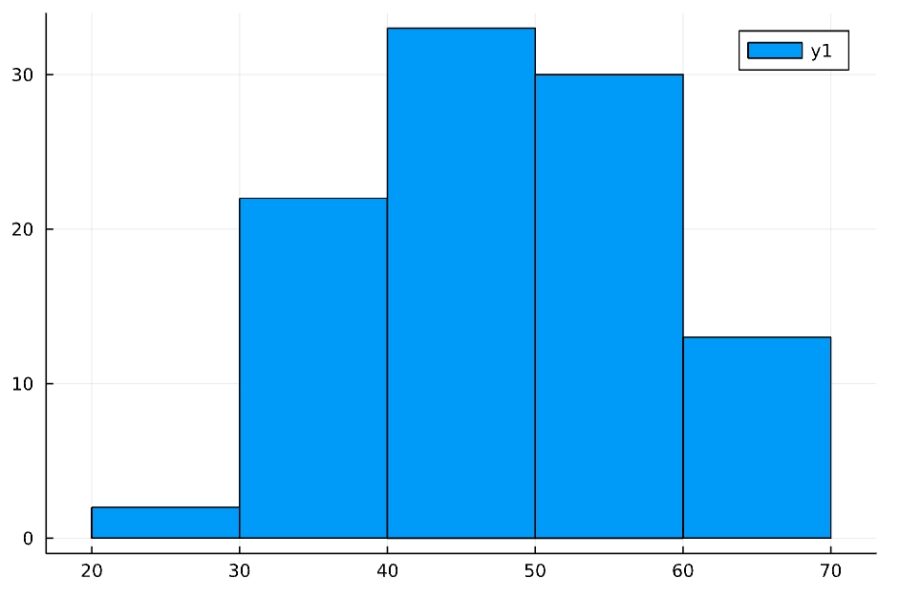
このデータは、平均50、分散10の正規分布から得られたものではないか、と推測してみます。
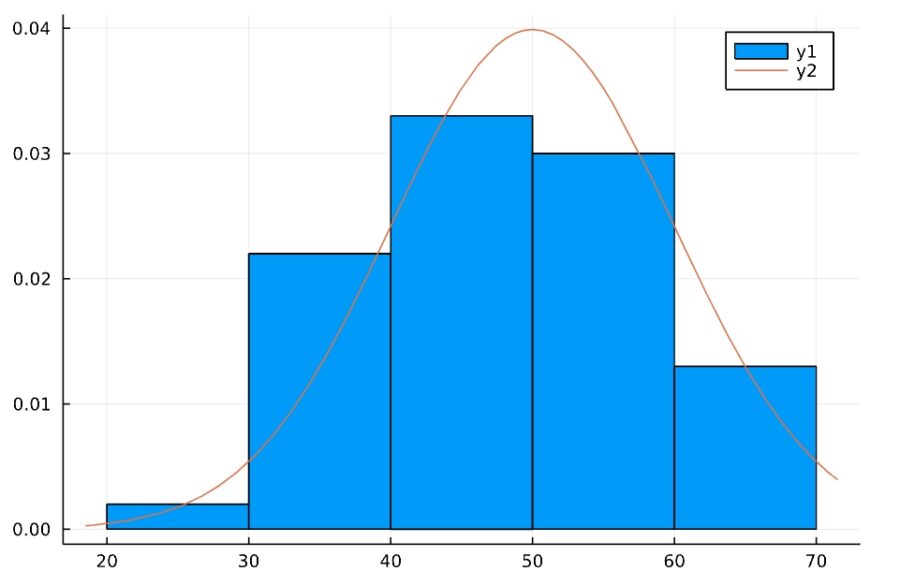
経験分布関数と理論的な正規分布を合わせて描いてみると、上の図のようになりました。かなり近いように見えますが、果たしてこの推論は妥当なのでしょうか。
このサンプルから得られる経験分布は、理論分布にフィットしていると言えるのでしょうか? それを検証するのに、適合度の検定、カイ二乗検定が利用できます。
適合度検定の考え方は、次のようなものです。
一般に、\(k\)個の取りうる値がある試行を、\(n\)回行ったとしましょう。
それぞれの値が観測された回数(サンプルの度数)を\(n_1,\dots,n_k\)とします。また、1回の試行でそれぞれの値を取る経験的な確率が\(p_1,\dots,p_k\)(多項分布)であったとします。
それぞれの値を取る理論的な確率を、\(\theta_1,\dots,\theta_k\)としましょう。調べたい仮説は、
\[H_0 : p_i = \theta_i \quad(i =1,\dots,k)\]
です。対立仮説\(H_1\)は、\(H_0\)が成り立たないこととします。
\(e_i = n \theta_i\)を、それぞれの値の理論的な期待値としましょう。帰無仮説\(H_0\)が正しいとき、統計量
\[\chi^2 = \sum_{i=1}^k \frac{(n_i -e_i)^2}{e_i}\]
は、\(n\)を大きくすると、自由度\(k-1\)のカイ二乗分布に近づくことが知られています。
この近似による適合度の検定は、ピアソンのカイ二乗検定と呼ばれるものです。
この考え方を、データと理論的な分布の問題に応用しましょう。
今回のデータでは、取りうる値は連続的ですが、実数全体を有限個の区間\(I_1,\dots,I_k\)に分けて考えれば良いです。
例えば、\((-\infty,40),(40,45),(45,50),(50,55),(55,60),(60,\infty)\)のように。それぞれの区間内に値を取るデータの個数を数えれば、\((n_1,\dots,n_6)=(24,18,15,20,10,13)\)となります。
想定する理論的な分布(ここでは正規分布)の累積分布関数を\(F\)としましょう。各区間に対応する理論的な確率\(\theta_i\)は、\(F\)を使って求めることができます。例えば、40以上45以下となる確率は\(\theta_2 = F(45)-F(40)\)です。
有限個の区間に分けて考えることで、経験的な頻度と理論的な確率を比較して、それらの適合度の検定が行なえますね。
Juliaによる計算例
ここからは、コンピュータ、Juliaを使って適合度検定、カイ二乗検定を実行してみましょう。
テストを100人に受けてもらった結果のサンプルを作ります。
1 2 3 4 | using Distributions, HypothesisTests, Random, Plots Random.seed!(2022) s = rand(Normal(50,10),100) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 100-element Vector{Float64}: 50.6912301164913 38.84399961848597 42.84480604223728 60.9769650429804 54.978651946367876 33.951339022096505 40.96806064167559 32.42960541746047 49.11909337153176 48.368593011534614 45.130463442688736 66.0313475290611 69.28907743700123 ⋮ 46.79927731213494 57.536857062367844 39.28597115377097 38.35659723735428 58.75013584844163 38.12985098735682 50.12197944102362 44.03918158496799 49.692328132341224 43.26677023980149 32.848246943470684 50.378377672704886 |
冒頭で示したヒストグラムは、このサンプルを使って作られました。
1 2 | histogram(s, bins=6,normalize=true) plot!(x-> pdf(Normal(50,10),x)) |

このサンプルによる経験分布が、正規分布\(\mathrm{Normal}(50,10)\)の理論分布に適合するか、カイ二乗検定してみましょう。
まず、サンプルがそれぞれの区間の値を取る回数をまとめたベクトル\((n_1,\dots,n_6)=(24,18,15,20,10,13)\)に変換する必要があります。これはサンプルから「count」を使うことで可能です。
区間の分け方は、40以下、40から60までは長さ5の等間隔、60以上としました。
1 2 3 4 | x = [count(y->(i<=y<i+5),s) for i in 40:5:55] pushfirst!(x,count(y->(y<40),s)) push!(x,count(y->(y>60),s)) x |
1 2 3 4 5 6 7 | 6-element Vector{Int64}: 24 18 15 20 10 13 |
累積分布関数を利用することで、各区間の値を取る理論的な確率\(\theta_0 = (\theta_1,\dots ,\theta_6)\)を求められます。
1 2 3 4 | theta0 = [cdf(Normal(50,10),i+5)-cdf(Normal(50,10),i) for i in 40:5:55] pushfirst!(theta0, cdf(Normal(50,10),40)) push!(theta0, 1-cdf(Normal(50,10),60)) theta0 |
1 2 3 4 5 6 7 | 6-element Vector{Float64}: 0.15865525393145702 0.14988228479452986 0.19146246127401312 0.19146246127401312 0.14988228479452992 0.15865525393145696 |
xの合計は100(サンプルサイズ)、theta0の合計は1(実数全体の確率)となっていることを、sum関数でチェックしておくと良いでしょう。
また、区間の分け方が悪く理論的な確率が小さくなりすぎると、\(e_i = n\theta_i\)が5以下となり、近似(カイ二乗検定)の妥当性が成り立たなくなることに注意しましょう。今回は、そうならないような区間の選び方をしました。
Hypothetistests.jlパッケージでは、「ChisqTest(x, theta0)」で帰無仮説を\(H_0 : p_i = \theta_i \quad(i =1,\dots,k)\)とするカイ二乗検定を行えます。
1 | ChisqTest(x, theta0) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.158655, 0.149882, 0.191462, 0.191462, 0.149882, 0.158655] point estimate: [0.24, 0.18, 0.15, 0.2, 0.1, 0.13] 95% confidence interval: [(0.15, 0.3397), (0.09, 0.2797), (0.06, 0.2497), (0.11, 0.2997), (0.01, 0.1997), (0.04, 0.2297)] Test summary: outcome with 95% confidence: fail to reject h_0 one-sided p-value: 0.1624 Details: Sample size: 100 statistic: 7.889500604079792 degrees of freedom: 5 residuals: [2.04222, 0.777941, -0.947574, 0.195115, -1.28846, -0.719411] std. residuals: [2.22646, 0.843737, -1.05381, 0.216991, -1.39744, -0.784314] |
帰無仮説は棄却されない、つまりデータは正規分布に従っている可能性があることが示せました。
この検定では、確率分布での各区間での形状の違いは検出できないことに気をつけましょう。あくまで、各区間での理論的な確率がサンプルの度数とマッチするかどうかを調べているだけです。
確率(面積)が等しいけれども、曲線として異なるような違いは検出されません。
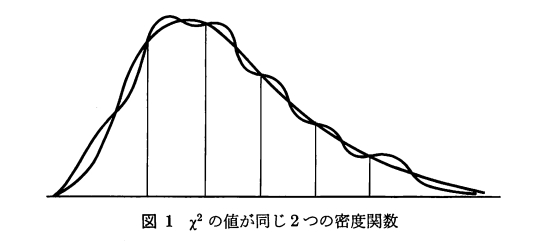
画像引用:ホーエル「入門数理統計学」 第9章 適合度の検定
別の例として、次のようなデータが得られたとしましょう。(自由度1のt分布、コーシー分布によるサンプルです。)
1 2 | Random.seed!(2022) s = rand(TDist(1),100) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 100-element Vector{Float64}: 16.152155646068486 1.6016516881079645 3.655678453995231 -3.669493976554157 -12.65095123291242 -0.3504802249145816 -8.99242194318552 0.3410538631454207 -2.1573730489649976 -0.6406845062994627 -2.9357114630087167 11.004585523845993 -1.2706724304598294 ⋮ 1.7864222894293502 -0.31944381026082946 110.88377026638199 0.02605006656255294 -0.9547951169066855 -0.2882853928376707 -0.2968785914822648 0.07973048320038773 0.10722654838126307 -2.4382997456912285 -2.8329314154232095 2.153461724288959 |
1 2 | histogram(s, bins=10,normalize=true) plot!(x-> pdf(Normal(mean(s),std(s)),x)) |

最尤推定量としてサンプル平均と分散を利用した正規分布は、このデータとマッチしているのでしょうか。検定によって調べてみましょう。
実数全体の区間分けとして、-10以下、-10から10までは長さ5の等間隔、10以上という分け方を考えます。
それぞれの区間に値を取るデータの個数は、次の通りです。
1 2 3 4 | x = [count(y->(i<=y<i+5),s) for i in -10:5:5] pushfirst!(x,count(y->(y<-10),s)) push!(x,count(y->(y>10),s)) x |
1 2 3 4 5 6 7 | 6-element Vector{Int64}: 4 3 46 37 6 4 |
正規分布を理論的な分布とするとき、各区間に対応する確率は次の通りです。
1 2 3 4 5 | d = Normal(mean(s),std(s)) theta0 = [cdf(d,i+5)-cdf(d,i) for i in -10:5:5] pushfirst!(theta0, cdf(d,-10)) push!(theta0, 1-cdf(d,10)) theta0 |
1 2 3 4 5 6 7 | 6-element Vector{Float64}: 0.26560618206854636 0.11211928769150908 0.12356565549121029 0.1234409049849915 0.11178004635994776 0.263487923403795 |
この数字を見るだけでも、データよりも正規分布は裾が厚いことが感じられますね。
適合度検定を行うと、次のようになりました。
1 | ChisqTest(x, theta0) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Pearson's Chi-square Test ------------------------- Population details: parameter of interest: Multinomial Probabilities value under h_0: [0.265606, 0.112119, 0.123566, 0.123441, 0.11178, 0.263488] point estimate: [0.24, 0.18, 0.15, 0.2, 0.1, 0.13] 95% confidence interval: [(0.15, 0.3397), (0.09, 0.2797), (0.06, 0.2497), (0.11, 0.2997), (0.01, 0.1997), (0.04, 0.2297)] Test summary: outcome with 95% confidence: reject h_0 one-sided p-value: 0.0054 Details: Sample size: 100 statistic: 16.55724483142758 degrees of freedom: 5 residuals: [-0.496851, 2.02724, 0.752003, 2.17905, -0.352342, -2.60053] std. residuals: [-0.579777, 2.15144, 0.803267, 2.32743, -0.373856, -3.0302] |
ここで注意したいのが、理論分布\(F\)の\(r\)個のパラメータが未知であり、それを最尤推定量によって推測するときは、検定に用いる自由度が変化することです。
そのとき、統計量\(\chi ^2\)は自由度\(\nu = k-1\)ではなく、\(\nu = k -r-1\)のカイ二乗分布に従うことが知られています。
したがって、今回は正規分布の平均、分散という2つのパラメータを考えたので、自由度は\(6-1=5\)ではなく\(6-2-1=3\)を考える必要があります。
HypothesisTests.jlのChisqTestでは、自由度は指定できないようです。しかしながら、統計量は約17と求められいます。
自由度3のカイ二乗分布の累積分布関数が\(1-\alpha =0.95\)となる値(臨界値)\(c\)は、
1 | quantile(Chisq(3),0.95) |
1 | 7.814727903251177 |
です。検定統計量の約17はこれを上回っているので、帰無仮説は棄却されます。
よって、このサンプルは正規分布に従っているとは考えがたいことが示せました。
以上、理論分布(正規分布)の当てはめの適合度検定について、Juliaによる計算例を紹介してきました。
今回は理論分布として正規分布のみを考えましたが、同じ手順によって、理論分布による当てはめが妥当かどうか検定できますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)