どうも、木村(@kimu3_slime)です。
今回は、抜き取り検査、OC曲線とは何か、Juliaによる実践例をもとに紹介します。
抜き取り検査
抜き取り検査(acceptance sampling)は、工業製品など大量の生産物が不良品を含みすぎないかどうかを、そこからtリ出した少数のサンプルをもとに判断する検査です。
たとえば1ロット(1まとまり)1000個のネジを作り、その長さ(cm)が次のようであったとしましょう。
1 2 3 4 | using Distributions, Plots, Random Random.seed!(2022) x = rand(Normal(10,0.05),1000) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 1000-element Vector{Float64}: 10.003456150582457 9.94421999809243 9.964224030211186 10.054884825214902 10.02489325973184 9.919756695110483 9.954840303208378 9.912148027087301 9.995595466857658 9.991842965057673 9.975652317213443 10.080156737645305 10.096445387185007 ⋮ 10.064302344981755 10.028005553505979 10.085731947696551 10.03670139774842 10.001567423386525 9.915551771891801 10.076122554493042 10.050421303921842 10.015964934151237 10.036566370113123 9.95133478978373 9.94622379129642 |
そして、10(cm)から誤差が約0.1cmを超えるものを不良品とするとしましょう。
このとき、ロットから20個のサンプルを取り出し、不良品が1つ含まれるかどうかで、そのロットが合格か不合格か判断するのは、どのくらい妥当なのでしょうか?
抜き取り検査では、不良品(defectives)の個数\(x\)が、許容個数\(c\)(acceptance number)以下であるかどうかによって、ロットを合格(accept)とするか不合格(reject)とするかを決めます。\(x \leq c\)なら合格、\(x>c\)なら不合格です。
例えば不良品の基準を10(cm)から誤差が約0.1cmを超えるもの、許容個数を\(1\)とするとき、20個のサンプル
1 | s = rand(x,20) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | 20-element Vector{Float64}: 9.922400467041394 9.934728042199371 9.95353274957312 10.022188221072462 10.003456150582457 9.980410538509055 10.076164182885538 9.91732512816269 9.990010239866903 10.083399453028186 9.925501511174676 10.08925288717408 9.99752860636217 9.945708438840613 10.09673239477927 10.061537494295626 9.949123881953046 9.892182909273245 9.932938233945395 10.087868792485734 |
は合格です。不良品は「9.892182909273245」のみで、不良品の個数は1個なので。
OC曲線
ロットが合格となる確率について、理論的に考えていきましょう。
ロットのサイズを\(N\)、サンプルのサイズを\(n\)、許容個数を\(c\)、不良品の個数を\(X\)とします。このとき、不良品の個数が従う確率分布は、超幾何分布であることが知られています。ロットが合格になる確率は、
\[P(X \leq c) =\sum_{k=0}^c \frac{C(M,k)C(N-M,n-k)}{C(N,n)}\]
です。
ここで\(M\)はロットに含まれる不良品の個数、\(C\)は2項係数です。
そして、不良品率(defect rate)を\(\theta = \frac{M}{N}\)と置いて書き直すと、
\[P_\theta(X \leq c) =\sum_{k=0}^c \frac{C(N\theta,k)C(N-N\theta,n-k)}{C(N,n)}\]
となります。\(N,n, c\)を固定して、これを\(\theta\)の関数と見るとき、そのグラフはOC曲線(OC curve; operating characteristic curve ,検査特性曲線)と呼ばれます。
例えば\(N=1000, n=20, c=1\)のときのOC曲線は次の通りです。「Hypergeometric(s, f, n)」で超幾何分布、「cdf」でその累積分布が計算できます。
1 2 3 4 5 6 7 | N = 1000 n = 20 c = 1 θ = 0:1/100:1 f(x) = cdf(Hypergeometric(N*x, N-N*x, n),c) plot(θ,f,xlabel="defect ratio θ", ylabel="probability of acceptance") |
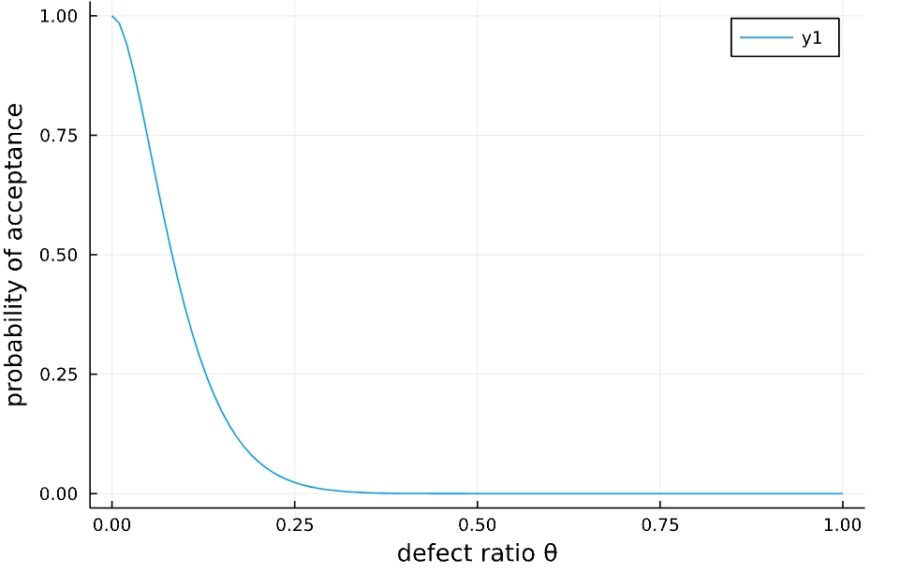
例えば、\(\theta =0.02\)のとき、関数の値は
1 | f(0.02) |
1 | 0.9417807413678954 |
となりますが、これはロットの不良品率が\(0.02\)であるとき、抜き取り検査によってロットが合格になる確率は約\(0.94\)であることを意味しています。
\(N\)に対して\(n, \theta\)が十分小さいとき、ロットが合格になる確率はポアソン分布\(\mathrm{Poisson}(n\theta)\)で近似できることが知られています。
\[P_\theta(X \leq c) \sim e^{-n\theta}\sum_{k=0}^c \frac{(n\theta)^k}{k!}\]
実際グラフを描いて比較してみると、特に\(\theta < 0.1\)のときは良い近似になっていることがわかります。
1 2 3 4 5 6 7 8 9 | N = 1000 n = 20 c = 1 θ = 0:1/100:1 f(x) = cdf(Hypergeometric(N*x, N-N*x, n),c) plot(θ,f,label = "Hypergeometric") g(x) = cdf(Poisson(n*x),c) plot!(θ,g, label = "Poisson" ,xlabel="defect ratio θ", ylabel="probability of acceptance") |
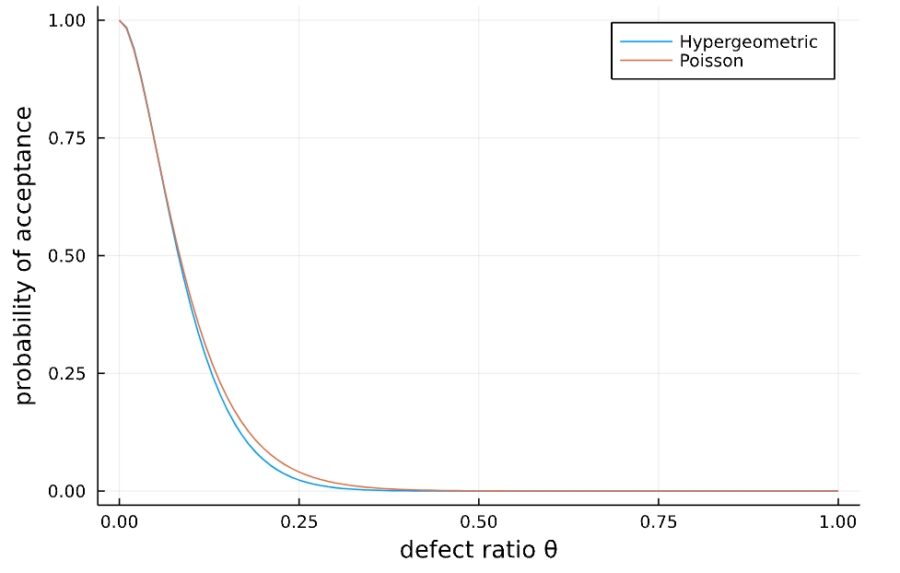
以降では、ポアソン近似を用いて計算してみましょう。
抜き取り検査の考え方は、仮説検定の考え方によく似ています。
仮説検定で二種類の過誤があったように、抜き取り検査には二種類のリスクがあります。
1 2 3 4 5 6 7 8 | N = 1000 n = 20 c = 1 f(x) = cdf(Poisson(n*x),c) plot(f,xlims=[0,0.25], xlabel="defect ratio θ", ylabel="probability of acceptance") vline!([0.02,0.15], xticks=([0,0.02,0.15,0.25],[0,0.02,0.15,0.25])) |
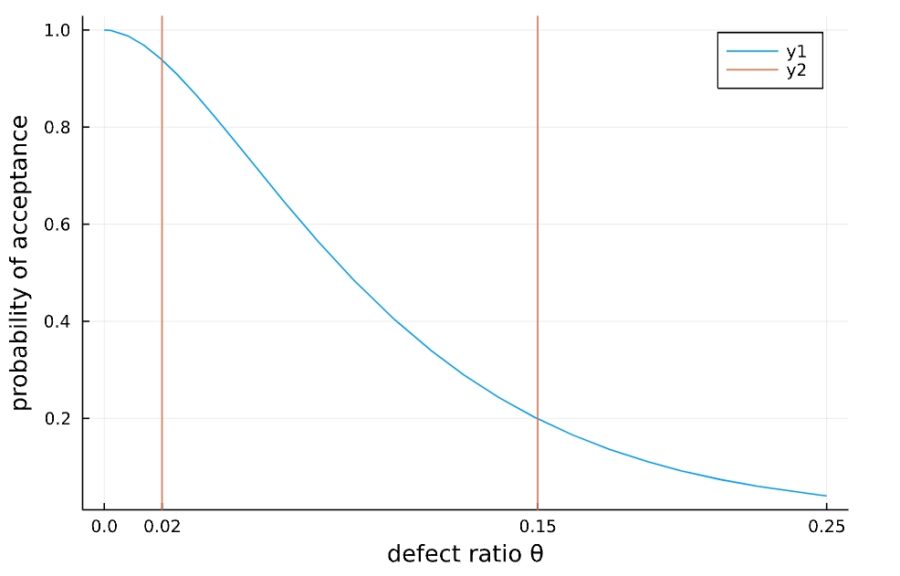
不良品率が\(\theta_0 =0.02\)、\(\theta _1 = 0.15\)のところに垂直線を引きました。
\(\theta_0\)より小さな不良品率を、良い品質のロットと生産者は考えるとしましょう。この基準\(\theta_0\)を合格品質水準(AQL; acceptable quality level)と呼びます。
仮に不良品率が合格品質水準のロットであったとしても、抜き取り検査によって
1 | α = 1-f(0.02) |
1 | 0.061551935550104964 |
約6%が不合格となります。合格ロット(合格品質水準を超えるロット)を、不合格とする確率\(\alpha\)は、生産者リスク(producer’s risk)と呼ばれるものです。これは検定でいう第一種の過誤に対応します。
一方で、\(\theta_1\)より大きな不良品率を持つロットを、消費者は受け入れたくないとしましょう。\(\theta_1\)を不合格品質水準(ROL; rejectable quality level, LTPD)と呼びます。
仮に不良品率が不合格品質水準のロットであったとしても、抜き取り検査によって
1 | β = f(0.15) |
1 | 0.19914827347145578 |
約20%が合格になります。不合格ロット(不合格品質水準より悪いロット)が合格となる確率は、消費者リスク(consumer’s risk)と呼ばれるものです。検定でいう、第二種の過誤に対応します。
Juliaによる実践例
コンピュータ、Juliaによって抜き取り検査を実験し、OC曲線や生産者・消費者リスクの意味を確かめてみましょう。
冒頭で示した\(N=1000\)個のネジを1つのロットとし、そこから\(n=20\)個のサンプルを取り出し、許容個数を\(c=1\)とします。
サンプルに含まれる不良品の個数は
1 | length(s)-count(i->(10-0.1<=i<=10+0.1),s) |
1 | 1 |
といったように数えることができます。
ロットの不良品率が合格品質水準(\(\theta_0 =0.02\))となるような、不良品の範囲を設定しましょう。
今回は正規分布に従う乱数によってロットを生成しているので、そのような範囲が設定できます。
1 2 | γ = 1-0.02 r = quantile(Normal(10,0.05),(1+γ)/2)-10 |
1 | 0.11631739370204208 |
不良品の個数をカウントする関数、不良品率を求める関数を作りましょう。
1 2 3 | function count_defective(s) length(s)-count(i->(10-r<=i<=10+r),s) end |
1 2 3 | function defect_rate(s) count_defective(s)/length(s) end |
試しにロットを10個作り、不良品率が約0.02となることを確認してみましょう。
1 2 3 4 | for i in 1:10 x = rand(Normal(10,0.05),1000) println(defect_rate(x)) end |
1 2 3 4 5 6 7 8 9 10 | 0.014 0.023 0.021 0.017 0.016 0.023 0.023 0.02 0.015 0.027 |
また、抜き取り検査が合格か不合格か判別する関数を作ります。
1 2 3 4 5 6 7 | function acceptance_sampling(s,c) if count_defective(s) <= c return 0 else return 1 end end |
合格なら0、不合格なら1としました。さきほどのサンプルは
1 | acceptance_sampling(s,1) |
1 | 0 |
となるので合格です。
さまざまなロットとサンプルで抜き取り検査を行い、ロットの不良品率が\(\theta_0 =0.02\)のとき、抜き取り検査によって不合格となる割合を計算します。
1 2 3 4 5 6 7 8 9 10 11 | k=10^5 acc = 0 for i in 1:k x = rand(Normal(10,0.05),1000) s = rand(x,20) if acceptance_sampling(s,1) == 0 acc += 1 else end end 1-acc/k |
1 | 0.06245999999999996 |
これが生産者リスク\(\alpha \)の意味ですね。
同様に、不良品率が\(\theta_1 =0.15\)(不合格品質水準)のロットからサンプルを抜き取り検査することを繰り返し、合格となった割合を計算します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | γ = 1-0.15 r = quantile(Normal(10,0.05),(1+γ)/2)-10 k=10^5 acc = 0 for i in 1:k x = rand(Normal(10,0.05),1000) s = rand(x,20) if acceptance_sampling(s,1) == 0 acc += 1 else end end acc/k |
1 | 0.17922 |
これが生産者リスクの意味ですね。
「約18%が不良品であることを生産者は受け入れる」といった誤解をしないように気をつけましょう。ロットの不良品率が15%であるにもかかわらず、抜き取り検査をすり抜けて合格になってしまう確率が約18%という意味です。
サンプルサイズ\(n\)や許容個数\(c\)を変えることで、消費者リスクや生産者リスクは変わります。
1 2 3 4 5 6 7 8 9 10 | N = 1000 c = 1 k=100 plot() for i in 10:20:k f(x) = cdf(Poisson(i*x),c) plot!(f,xlims=[0,1], label="$i") end plot!() |

サンプルサイズを増やせば消費者リスクは下がりますが、その分サンプルを調べるコストが生産者側にかかる、というトレードオフの関係です。
指定された合格品質水準に対し、サンプルサイズをできるだけ小さくする\(n,c\)は数値計算によって表にまとめられています。詳しくは「入門数理統計学」など。
以上、抜き取り検査、OC曲線とは何か、Juliaによる実践例をもとに紹介してきました。
統計学、検定の考え方の応用として、少ないサンプルで不良品のリスクできるだけ減らす抜き取り検査の考え方は、知っておくと面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
統計的仮説検定とは:平均の検定、t検定を例に、Juliaを使って
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に