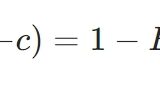t分布とその性質、Juliaによる計算方法

どうも、木村（@kimu3_slime）です。

今回は、t分布とその性質、Juliaによる計算方法を紹介します。

t分布とは
t分布の性質
累積分布関数の計算
こちらもおすすめ

t分布とは

スチューデントのt分布（t-distribution）は、確率密度関数

\[f(x)= \frac{\Gamma(\frac{\nu +1}{2})}{\sqrt{\nu \pi} \Gamma (\frac{\nu}{2})} (1+\frac{x^2}{\nu})^{-\frac{\nu+1}{2}}\]

を持つ確率分布です。ここで$\Gamma$はガンマ関数です。

パラメータ$\nu$（ニュー）は1以上の自然数で、自由度（degrees of freedom）と呼ばれています。

少し複雑な式に見えるかもしれませんが、およそ$\frac{1}{1+x^2}$を調整した形です。

$f(x)=-f(x)$が成り立ち、$x=0$について対称なグラフ、偶関数となっています。

特に$\nu =1$のときは、$\Gamma(\frac{1}{2})= \sqrt{\pi}$、$\Gamma(1)=1$なので、

\[f(x)= \frac{1}{\pi} \frac{1}{1+x^2}\]

となります。このケースは、（標準）コーシー分布（Cauchy distribution）とも呼ばれるものです。

いくつかの自由度でのt分布のグラフを、コンピュータ、Juliaで描いてみましょう。

「TDist(ν)」で自由度$\nu$のt分布が表せます。その確率質量関数は、「pdf(TDist(ν),x)」です。

using Distributions, StatsPlots

function Tplot(k)
    p = plot()
    x = -5:0.1:5
    for n in 1:5:k
        f(x) = pdf(TDist(n),x)
        p = plot!(x,f,label="ν=$n", xlims=[-5,5])
    end
    p = plot!(Normal(0,1),label="Normal(0,1)")
    display(p)
end

Tplot(21)

using Distributions, StatsPlots

function Tplot(k)

p = plot()

x = -5:0.1:5

for n in 1:5:k

f(x) = pdf(TDist(n),x)

p = plot!(x,f,label="ν=$n", xlims=[-5,5])

end

p = plot!(Normal(0,1),label="Normal(0,1)")

display(p)

end

Tplot(21)

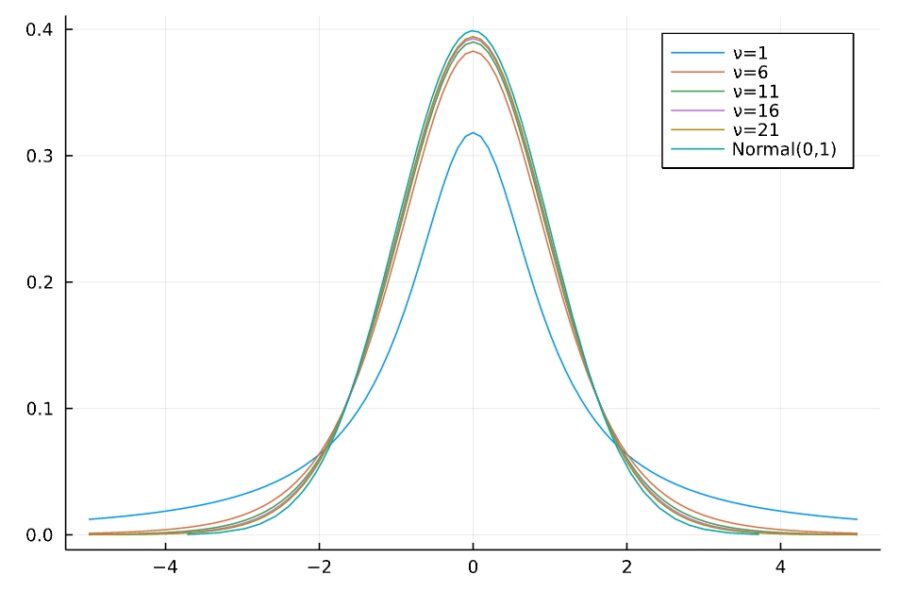
比較のために標準正規分布を描きました。$\nu$が大きくなると、t分布は標準正規分布に近づいていきます。逆に言えば、$\nu$が大きくないときは、正規分布との違いがある分布です。

t分布の性質

t分布を考えるメリットは、正規分布からのサンプルを変換するとそれに従うことがあります。

母集団分布$X$の分散$\sigma^2$がわかっているとき、それに従う独立な確率変数族$X_1,\dots,X_n$について、標準誤差

\[Z= \frac{M_n -\mu}{\frac{\sigma}{\sqrt{n}} }\]

は、正規分布に従うという良い性質があります。これは区間推定に応用されるものです。

この式における母集団分布の分散$\sigma^2$を、サンプル分散（不偏分散）

\[S^2 = \frac{1}{n-1}\sum_{k=1}^n(X_j -M_n)^2\]

に置き換えた確率変数

\[T= \frac{M_n -\mu}{\frac{S}{\sqrt{n}} }\]

について考えましょう。$\sigma$が$S$に変わったのですから、従う分布は正規分布ではなくなるはずです。実は$T$は、自由度$n-1$のt分布に従うことが知られています。

t分布を使えば、母集団分布の分散が未知の場合でも、正規分布に従うサンプルを使って平均の区間推定をすることができます。

正規分布に従う乱数によって得られたサンプルから$T$を計算し、それがt分布に従っているか確かめてみましょう。

「サンプル10個を取り出し、$T$を計算する」ことを10000回行い、それを正規化したヒストグラムとして図示し、自由度$10-1=9$のt分布と比較してみました。

d = Normal(50,10)
n = 10
k = 10000
T = zeros(k)
for i in 1:k
    x = rand(d,n)
    T[i] = (mean(x)-mean(d))/(std(x)/sqrt(n))
end
histogram(T, normalize=true)
plot!(TDist(n-1))

d = Normal(50,10)

n = 10

k = 10000

T = zeros(k)

for i in 1:k

x = rand(d,n)

T[i] = (mean(x)-mean(d))/(std(x)/sqrt(n))

end

histogram(T, normalize=true)

plot!(TDist(n-1))

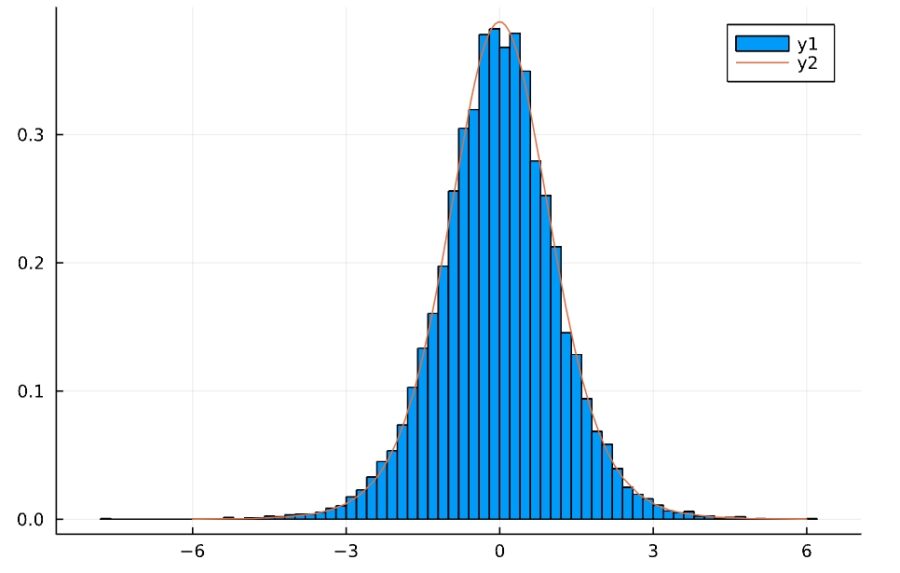
見事にt分布に従っていることがわかりますね。

累積分布関数の計算

t分布を使った区間推定などでは、その累積分布関数$F$に関する計算が必要です。

t分布の数値は教科書やウェブ上でまとまっていますが、ここではJuliaで求めてみましょう。

「cdf」で累積分布関数が作れます。

F(x) = cdf(TDist(19),x)
plot(F)

1 2	F(x) = cdf(TDist(19),x) plot(F)

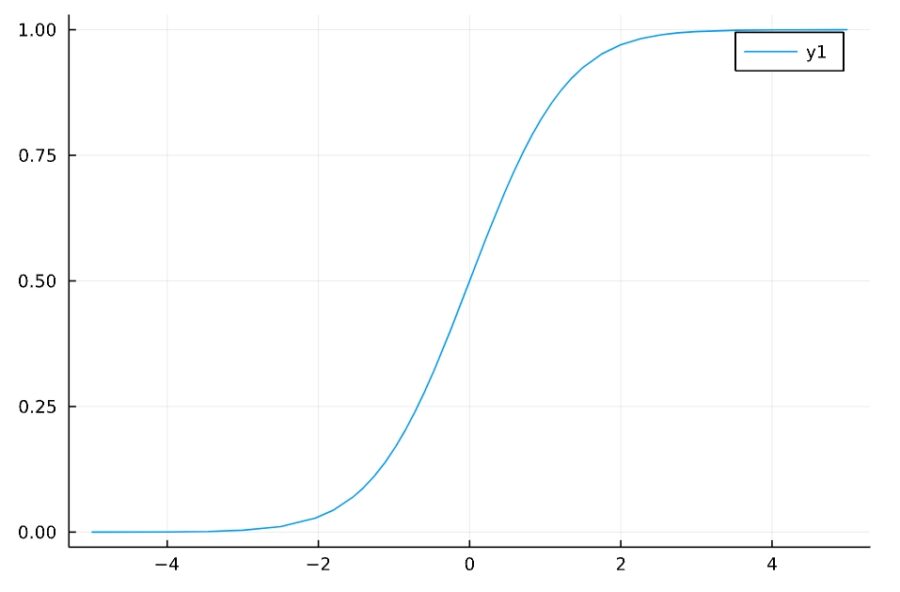
区間推定では、与えられた$\gamma$に対し、$F(c)-F(-c)=\gamma$を満たす$c$を求める必要があります。

$f$は偶関数なので、$F(-c)=1-F(c)$となり、$2F(c)=\gamma+1$、逆関数を使って$c= F^{-1}(\frac{\gamma+1}{2})$です。

「quantile」で累積分布関数の逆関数が求められます。

サンプルサイズが20のとき、つまり自由度19のt分布について、いくつかの$\gamma$について$c$を求めてみましょう。

n = 20
Γ = [0.9,0.95,0.99,0.999]
for γ in Γ
    println(quantile(TDist(n-1) , (γ+1)/2))
end

n = 20

Γ = [0.9,0.95,0.99,0.999]

for γ in Γ

println(quantile(TDist(n-1) , (γ+1)/2))

end

1.729132811521369
2.093024054408309
2.860934606464979
3.88340585259213

1.729132811521369

2.093024054408309

2.860934606464979

3.88340585259213

この結果は、t分布表の自由度19、信頼水準$\gamma$のところに対応したものです。確かに一致していますね。

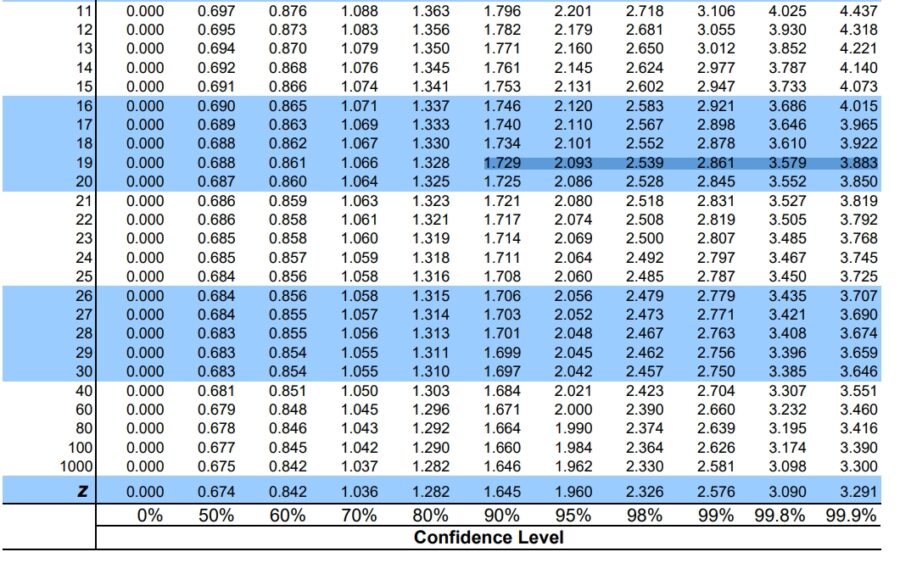
これによって、自由度や$\gamma$がいくつであろうが、$c$の値が計算できるようになりました。

以上、t分布とその性質、Juliaによる計算方法を紹介してきました。

確率密度関数が少し複雑に見えるかもしれないので、コンピュータを使って図を描いたり計算して馴染むと良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。

Probability and Statistics: Pearson New International Edition

posted with AmaQuick at 2022.03.24

DeGroot, Morris(著), Schervish, Mark(著)
Pearson Education Limited (2013-07-30T00:00:01Z)

￥10,792 (中古品)

Amazon.co.jpで詳細を見る

入門数理統計学

posted with AmaQuick at 2022.03.27

P.G.ホーエル(著), 浅井晃(翻訳), 村上正康(翻訳)
培風館 (1978-01-01T00:00:01Z)

￥5,280

Amazon.co.jpで詳細を見る

Advanced Engineering Mathematics

posted with AmaQuick at 2022.03.14

Kreyszig, Erwin(著)
John Wiley & Sons Inc (2011-05-03T00:00:01Z)

￥5,862 (中古品)

Amazon.co.jpで詳細を見る

こちらもおすすめ

広義積分とは何か、なぜ学ぶか（ガウス積分とガンマ関数）

独立な正規分布の和、平均が正規分布に従うこと（再生性）の証明

区間推定、信頼区間とは：分散既知の正規分布における平均の推定を例に

点推定、不偏推定量とは：平均と分散を例に、なぜn-1で割るのか