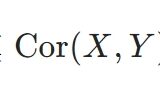どうも、木村(@kimu3_slime)です。
今回は、2変数の確率変数の分散とは何か、和と積の性質、証明を紹介します。
\[V(X+Y)=V(X)+V(Y)+2\mathrm{Cov}(X,Y)\]
\[V(XY) = V(X)V(Y)+(E(Y))^2 V(X) +(E(X))^2 V(Y)\]
2変数の分散
2つの確率変数\(X,Y\)があって、その和\(X+Y\)や積\(XY\)などの分散を考えたいとしましょう。
一般に、連続関数\(g\)を組み合わせた確率変数\(g(X,Y)\)の分散(variance)は、
\[V(g(X,Y)):= E((g(X,Y)-E(g(X,Y)))^2)\]
と定義されます。
期待値の線形性(和の性質、平行移動)を使って計算することで、
\[\begin{aligned} &\quad V(g(X,Y))\\&=E((g(X,Y))^2)-2 E(g(X,Y))E(g(X,Y))\\&\quad+(E(g(X,Y)))^2\\&=E((g(X,Y))^2) -(E(g(X,Y)))^2\end{aligned}\]
が成り立ちます。
和の性質
\(g(X,Y)=X+Y\)のケースで、
\[V(X+Y)=V(X)+V(Y)+\mathrm{Cov}(X,Y)\]
が成り立つことを紹介しましょう。ここで、\(\mathrm{Cov}\)は共分散
\[\mathrm{Cov}(X,Y)=E(XY)-E(X)E(Y)\]
です。
さきほど示した分散の関係式と、期待値の和の性質から
\[\begin{aligned} &\quad V(X+Y)\\ &= E((X+Y)^2) -(E(X+Y))^2\\&=E(X^2)+2E(XY)+E(Y^2)\\ &\quad -(E(X))^2-2E(X)E(Y)-(E(Y))^2 \\&=E(X^2)-(E(X))^2+E(Y^2)-(E(Y))^2\\ &\quad 2(E(XY)-E(X)E(Y))\\ &=V(X)+V(Y)+2\mathrm{Cov}(X,Y) \end{aligned}\]
となります。最後に1変数の分散の性質、共分散の性質(定義)を用いました。
\[V(X+Y)=V(X)+V(Y)\]
が成り立ちます。
積の性質
\(X,Y\)が独立であるとき、
\[V(XY) = V(X)V(Y)+(E(Y))^2 V(X) +(E(X))^2 V(Y)\]
が成り立つことを証明しましょう。
\(X,Y\)が独立であるときは、\(X^2 ,Y^2\)も独立になります。
一般に、\((X^2 \in A_1) = (X \in \sqrt{A_1})\)といったように言いかえられます(\(\sqrt{}\)は\(f(x)=x^2\)の逆像\(f^{-1}\)の意味)。したがって、\(A_1,A_2 \subset \mathbb{R}\)として、
\[\begin{aligned} &P(X^2 \in A_1 , Y^2 \in A_2) \\&=P(X \in \sqrt{A_1}, Y \in \sqrt{A_2}) \\&= P(X \in \sqrt{A_1}) P(Y \in \sqrt{A_2}) \\ &= P(X^2 \in A_1)P(Y^2 \in A_2)\end{aligned}\]
となるので独立です。
期待値の独立な変数の積に関する性質に注意して、
\[\begin{aligned} &V(XY)\\&=E(X^2Y^2) -(E(XY))^2 \\&= E(X^2)E(Y^2) -(E(X))^2 (E(Y))^2\\ &= (E(X^2 -(E(X))^2)+(E(X))^2) \\&\quad(E(Y^2 -(E(Y))^2)+(E(Y))^2)\\ &\quad-(E(X))^2 (E(Y))^2 \\&=(V(X)+(E(X))^2)(V(Y)+(E(Y))^2)\\ &\quad – (E(X))^2 (E(Y))^2 \\ &= V(X)V(Y)+(E(Y))^2 V(X) +(E(X))^2 V(Y)\end{aligned}\]
が成り立つことが示せました。
以上、2変数の確率変数の分散とは何か、和と積の性質、証明を紹介してきました。
ベルヌーイ分布の分散から二項分布の分散を求めるときに使える性質です。期待値の加法性は無条件で成り立ちますが、分散の加法性には共分散0(例えば独立性)という条件が必要であることに注意しましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)