どうも、木村(@kimu3_slime)です。
今回は、Juliaで確率分布に従う乱数、確率関数、累積分布関数を描く方法を紹介します。
前提知識:離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に、連続確率分布とは:一様分布、正規分布を例に
準備
StatsPlots, Distributionsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("StatsPlots") Pkg.add("Distributions") |
準備として、以下のコードを実行しておきます。
1 | using StatsPlots, Distributions, Random |
確率分布に従う乱数、グラフ、累積分布関数を描く方法
離散確率分布
Distributions.jlにはさまざまな確率分布が用意されています。
\(a\)以上\(b\)以下の値を取る離散確率分布は、DiscreteUniform(a,b)です。
「rand(確率分布,個数)」で、確率分布に従う乱数を指定した個数作ります。「histogram」で、それを図示しましょう。
「Random.seed!(シード)」で、乱数のシードを指定すると、実行結果が再現されます。
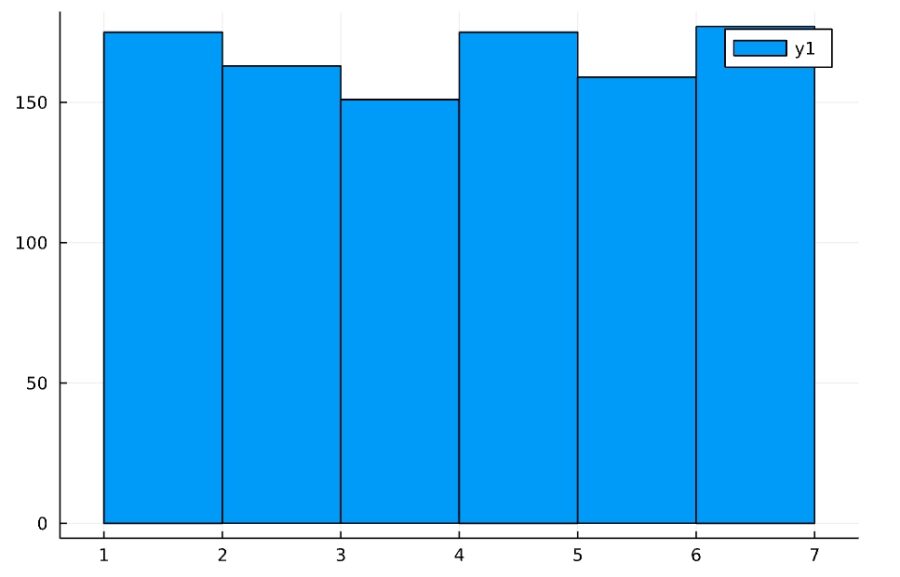
1 2 3 4 | Random.seed!(2022) d = DiscreteUniform(1,6) x = rand(d, 1000) histogram(x) |
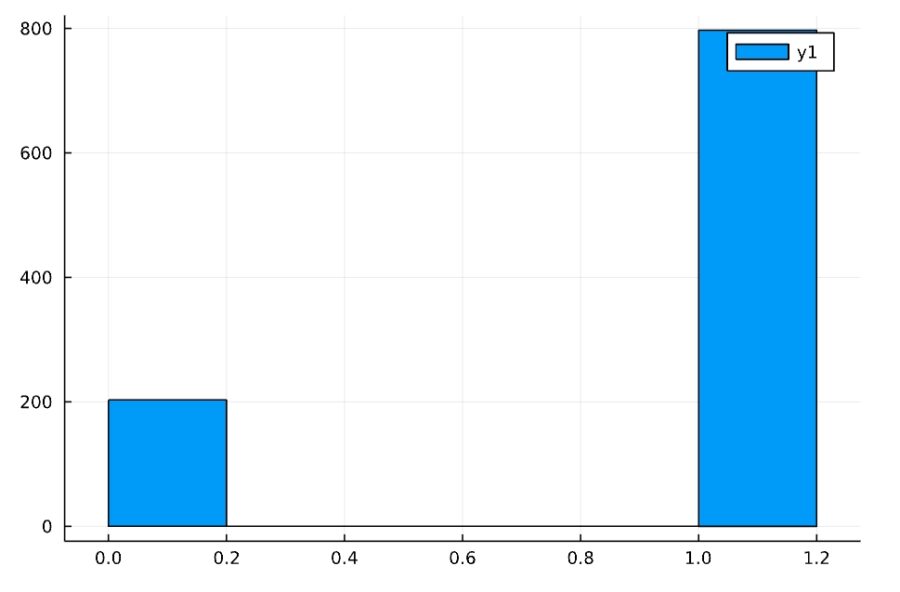
Bernoulli(p)が、確率pのベルヌーイ分布です。
1 2 3 4 | Random.seed!(2022) d = Bernoulli(0.8) x = rand(d, 1000) histogram(x) |
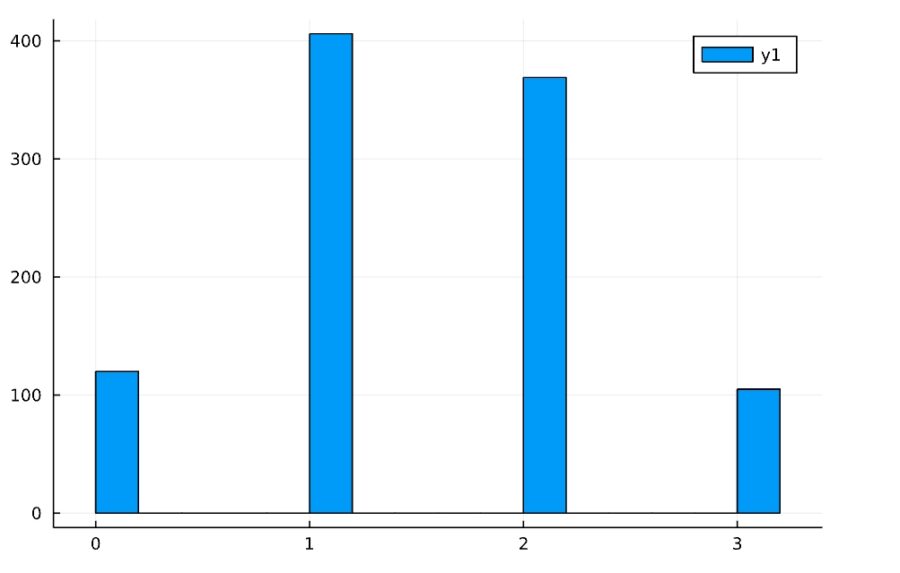
Binomial(n,p)が、試行回数n、確率pの二項分布です。
1 2 3 4 | Random.seed!(2022) d = Binomial(3,0.5) x = rand(d, 1000) histogram(x) |
Poisson(λ)が、一定時間における平均の発生頻度λのポアソン分布です。
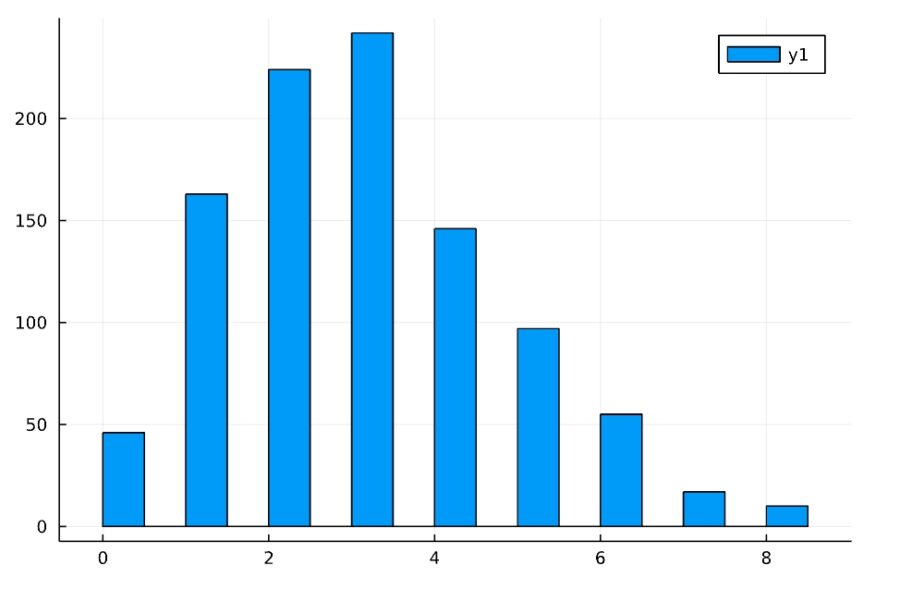
「plot(離散確率分布)」で、離散確率分布の確率質量関数をプロットできます。
1 | plot(DiscreteUniform(1,6)) |
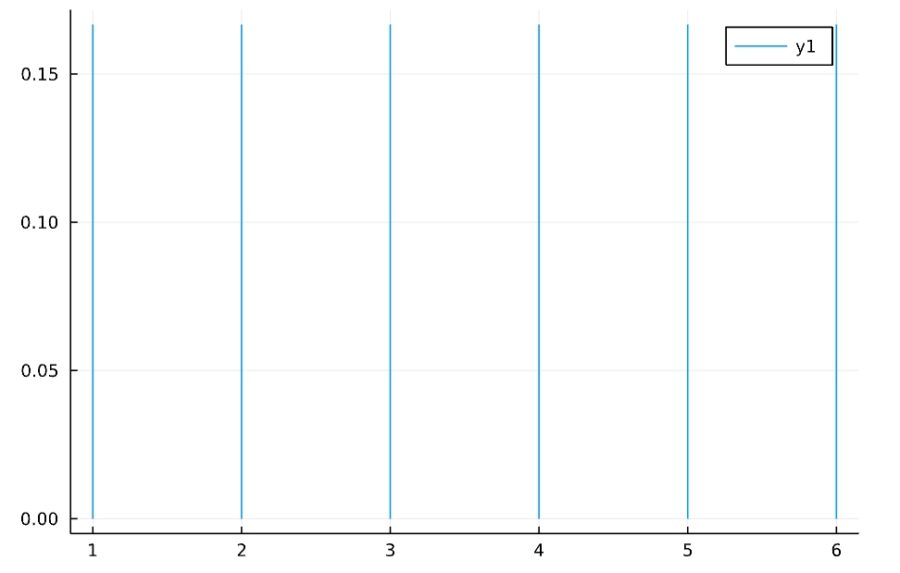
1 | plot(Bernoulli(0.8)) |
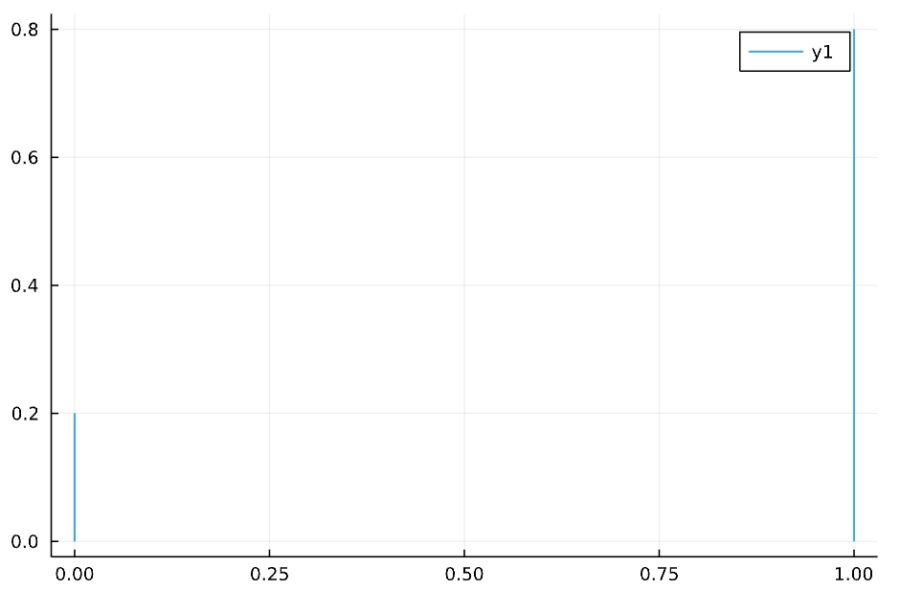
1 | plot(Binomial(100,0.5)) |
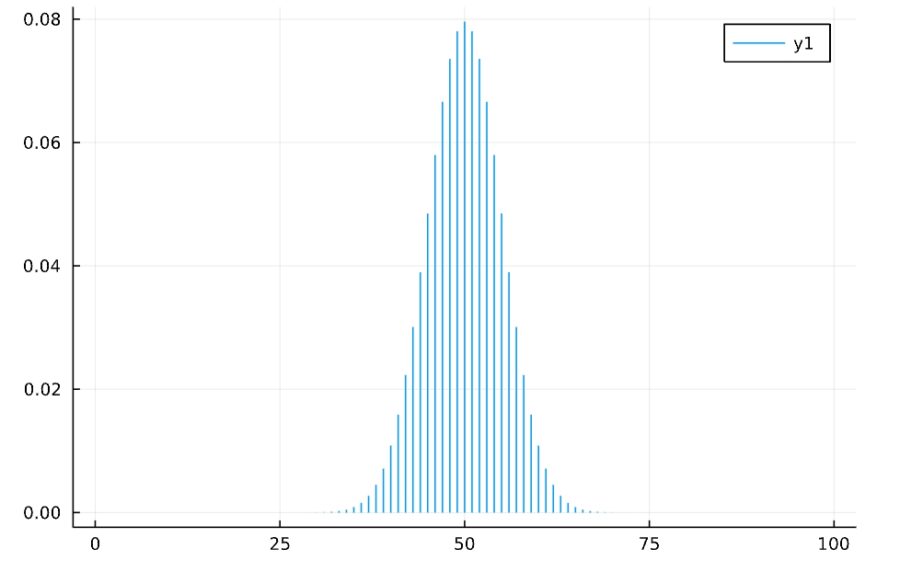
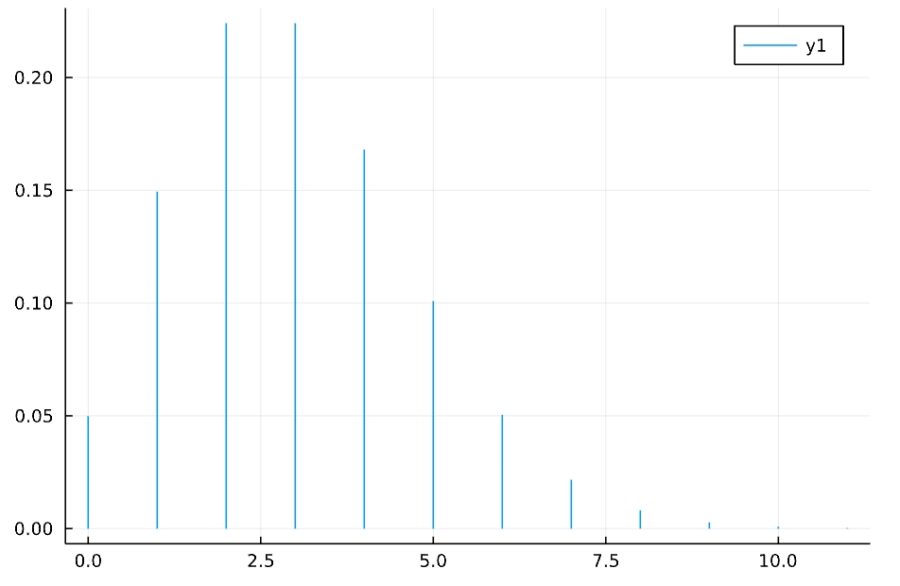
1 | plot(Poisson(3)) |
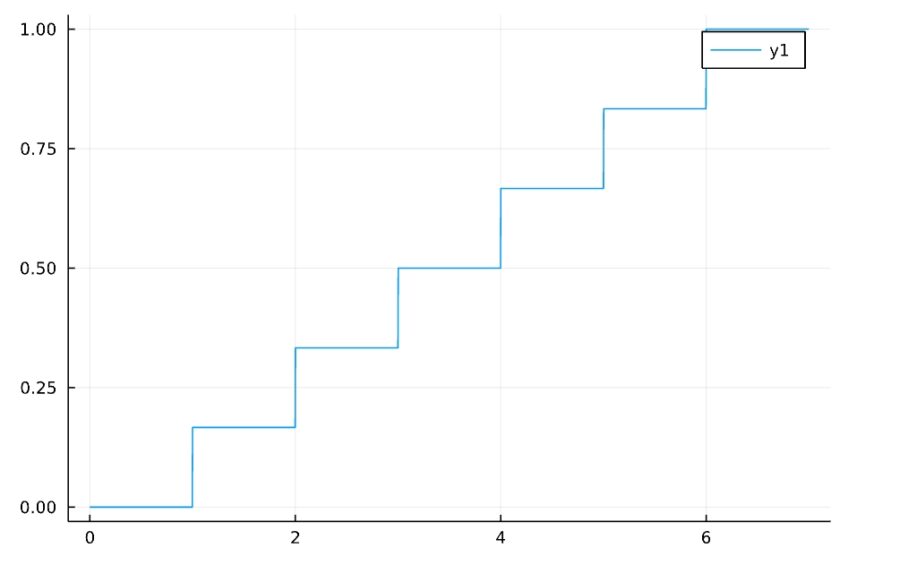
「cdf(確率分布,変数の値)」で、累積分布関数(cdf)が使えます。
1 2 | f(x) = cdf(DiscreteUniform(1,6),x) plot(f, xlims= [0,7]) |
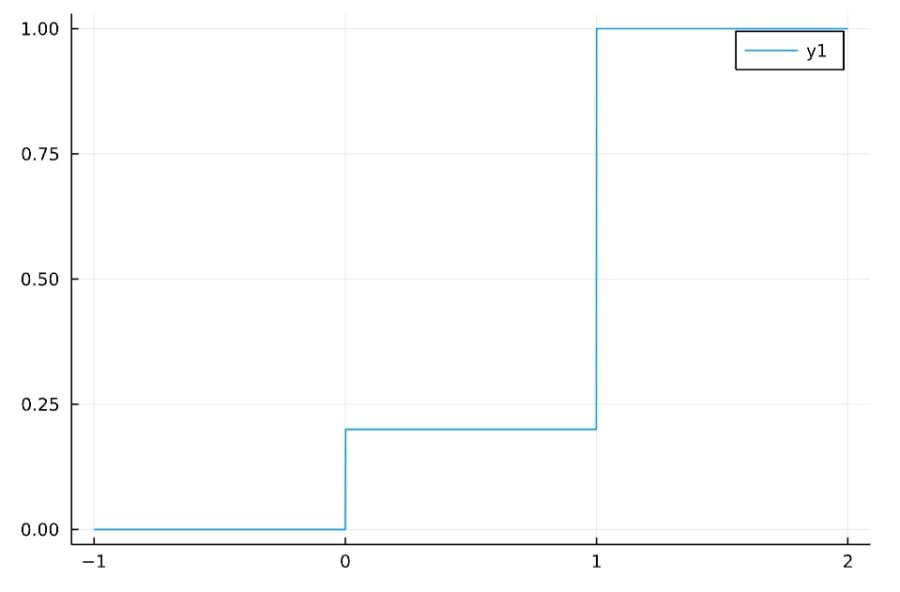
1 2 | f(x) = cdf(Bernoulli(0.8),x) plot(f, xlims= [-1,2]) |
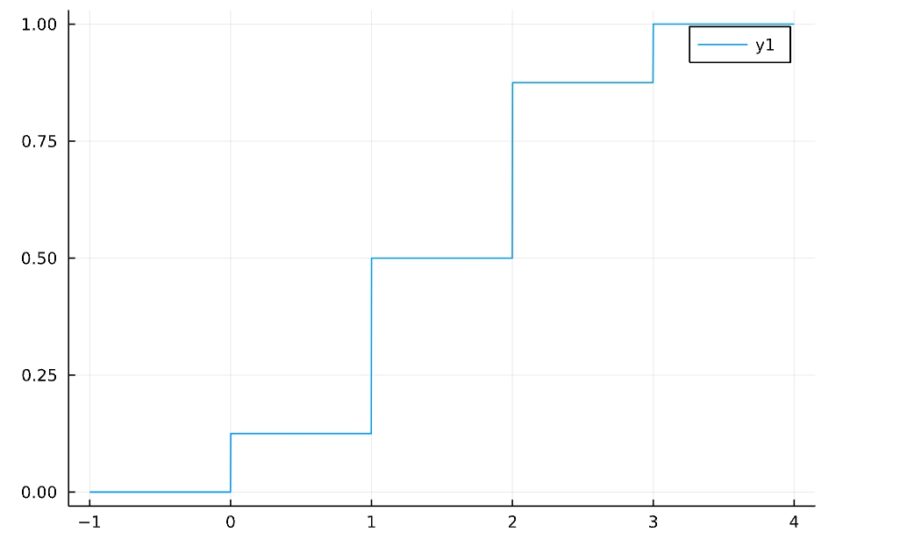
1 2 | f(x) = cdf(Binomial(3,0.5),x) plot(f, xlims= [-1,4]) |
1 2 | f(x) = cdf(Poisson(3),x) plot(f, xlims= [-1,10]) |
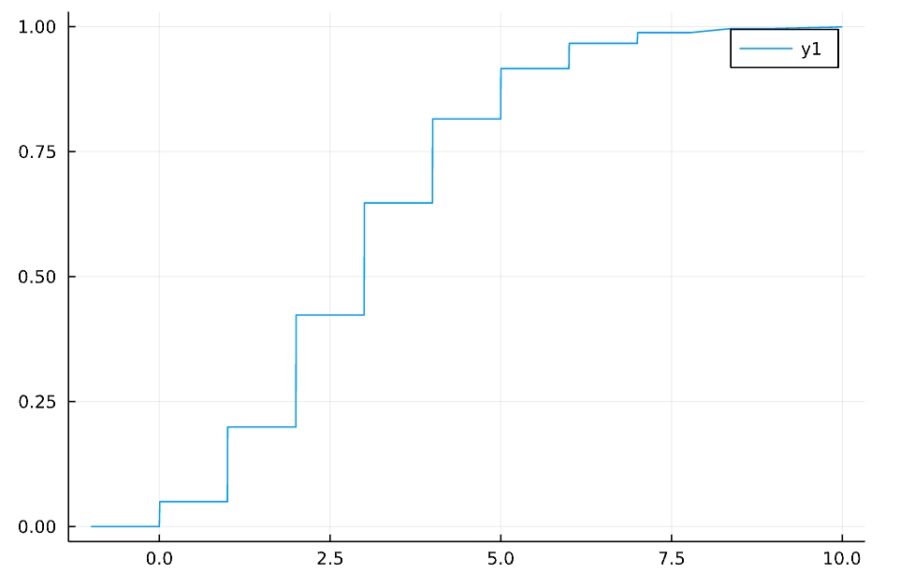
連続確率分布
連続確率分布についても、同様に描くことができます。
a以上b以下の連続一様分布は、Uniform(a,b)です。
1 2 3 4 | Random.seed!(2022) d = Uniform(0,360) x = rand(d, 500) histogram(x,bins=0:30:360) |
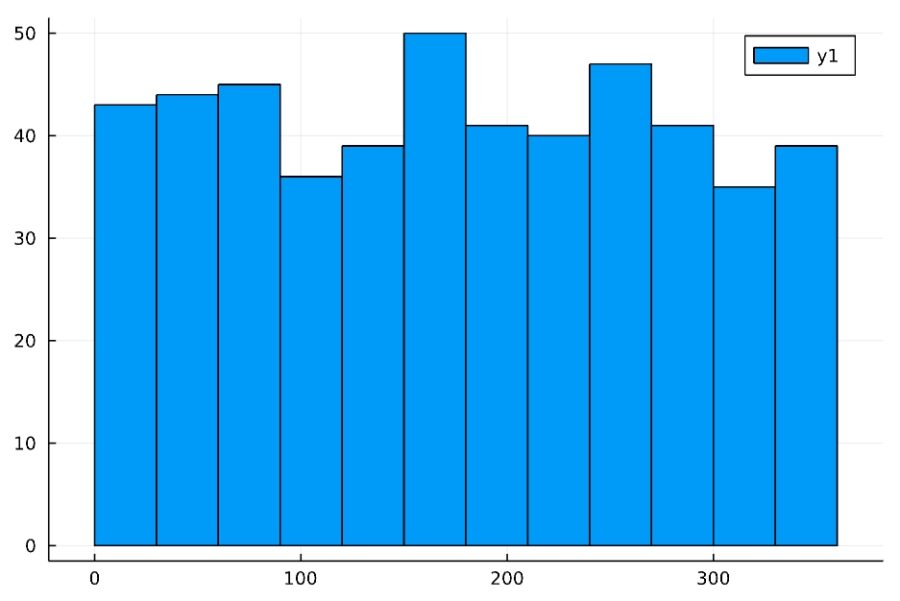
平均μ,分散σの正規分布は、Normal(μ,σ)です。
1 2 3 4 | Random.seed!(2022) d = Normal(50,20) x = rand(d, 100) histogram(x,bins=10) |
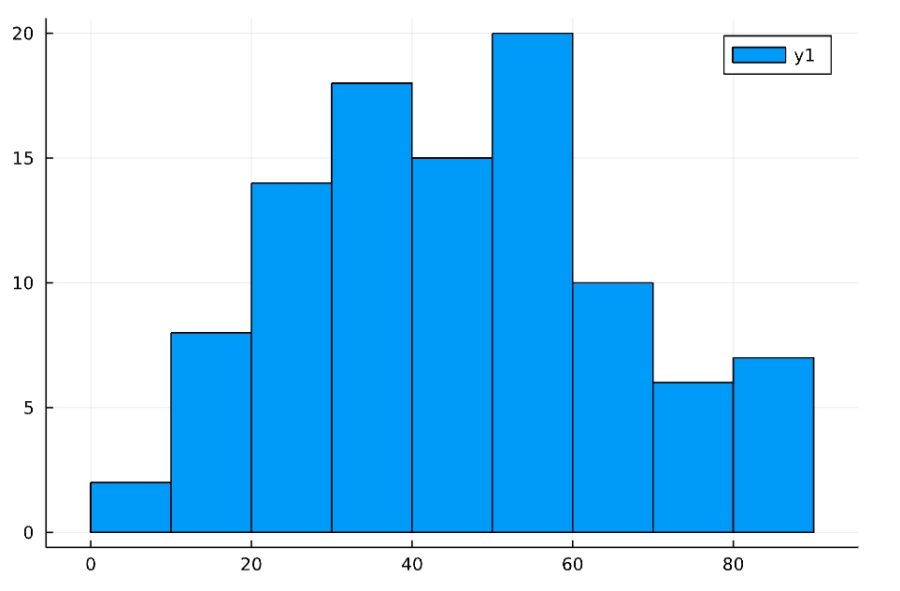
確率密度関数(pdf)の図示は、さきほどと変わって、「pdf(確率分布,変数の値)」です。
1 2 | f(x) = pdf(Uniform(0,360),x) plot(f,xlims=[-360,720]) |
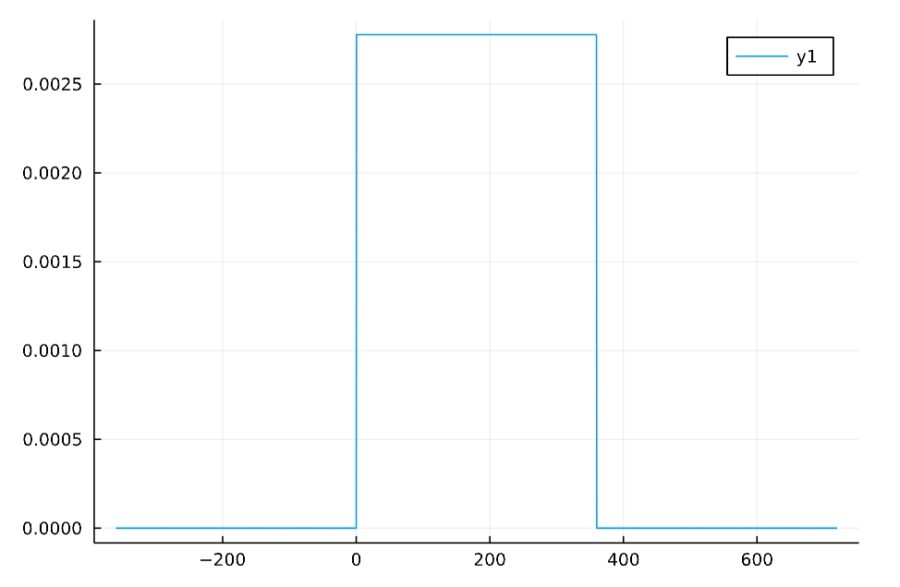
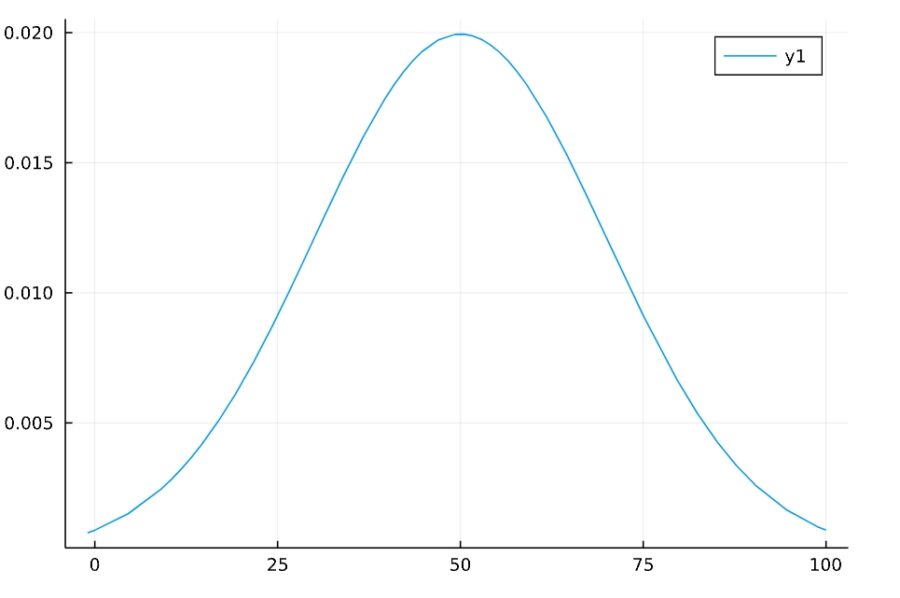
1 2 | f(x) = pdf(Normal(50,20),x) plot(f,xlims=[-1,100]) |
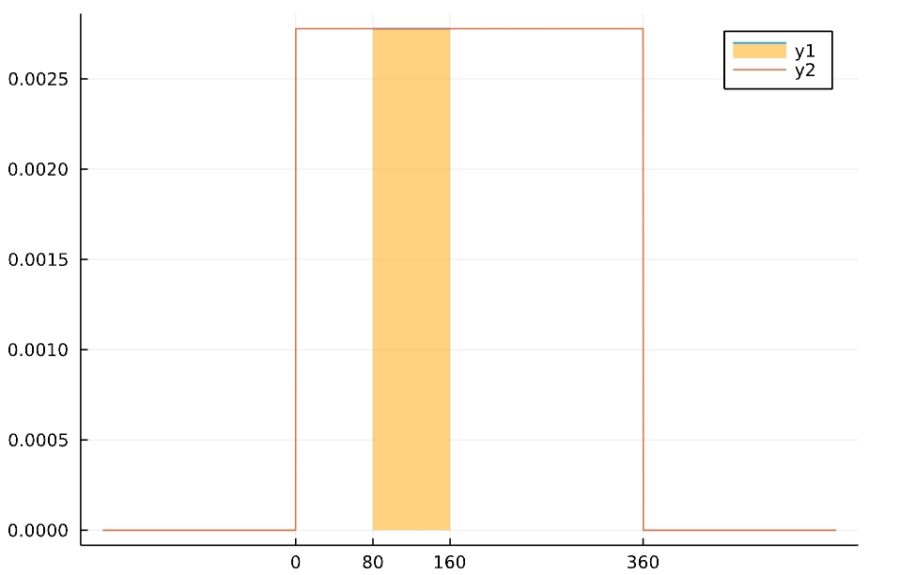
分布の一部分の区間を色を塗って図示するには、次のようにします。
前半のプロットのfillで、0と関数の値を、透明度0.5、オレンジ色で塗りつぶす指定をしました。それに確率密度関数全体を重ねて表示させる流れです。
1 2 3 | f(x) = pdf(Uniform(0,360),x) plot(f,xlims=[80,160],fill=(0, .5,:orange)) plot!(f,xlims=[-200,560],xticks =([0,80,160,360])) |
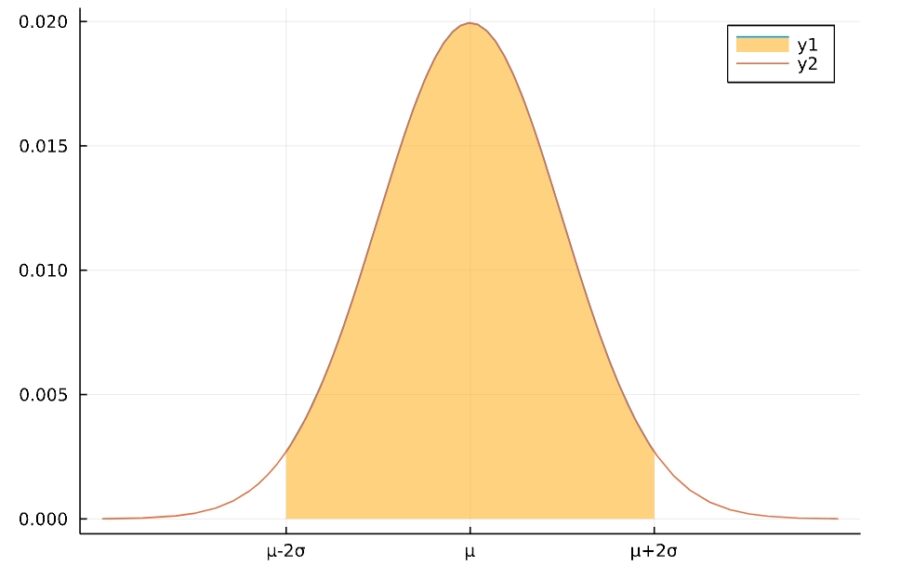
xticksを指定することで、x軸の目盛りの特定の値を指定した表示に変えることができます。
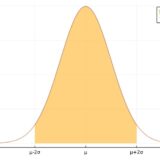
1 2 3 | f(x) = pdf(Normal(50,20),x) plot(f,xlims=[10,90],fill=(0, .5,:orange)) plot!(f,xlims=[-30,130],xticks =([10,50,90],["μ-2σ","μ","μ+2σ"])) |
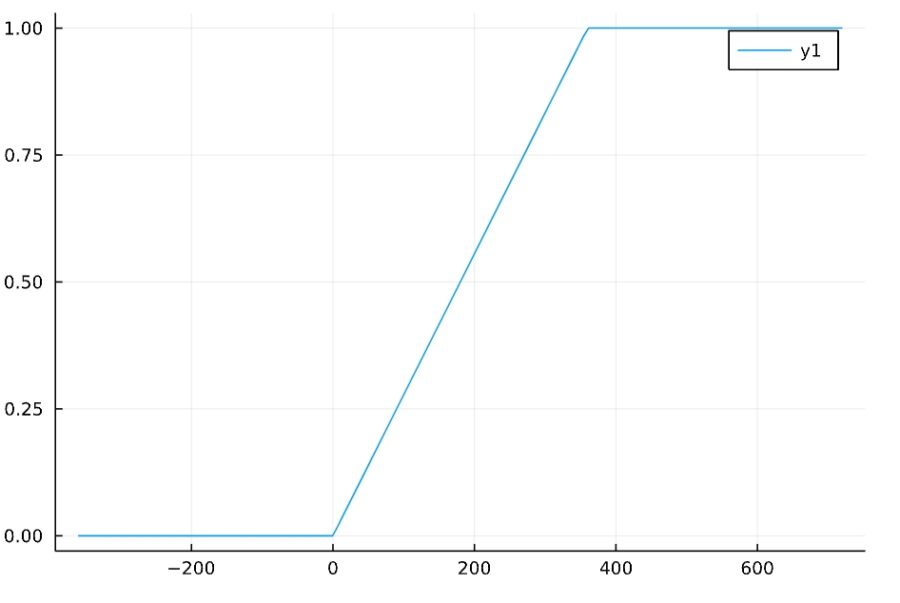
累積分布関数のプロットは、さきほどと同じです。
1 2 | f(x) = cdf(Uniform(0,360),x) plot(f,xlims = [-360,720]) |
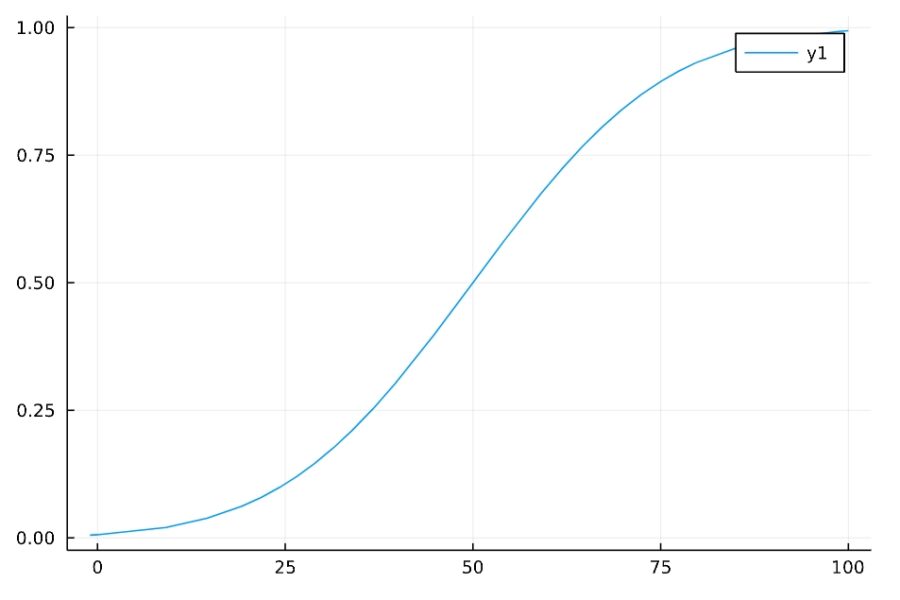
1 2 | f(x) = cdf(Normal(50,20),x) plot(f,xlims=[-1,100]) |
以上、Juliaで確率分布に従う乱数、グラフ、累積分布関数を描く方法を紹介してきました。
今回紹介した分布以外にもたくさんの分布が用意されているので、試してみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に
Juliaでデータのヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法