どうも、木村(@kimu3_slime)です。
今回は、Juliaでデータ(iris)のヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法を紹介します。
準備
RDatasets, StatsPlotsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("RDatasets") Pkg.add("StatsPlots") |
準備として、以下のコードを実行しておきます。
1 | using Statistics, RDatasets, StatsPlots |
データのヒストグラムを描く
RDatasets.jlには様々なデータセットがあります。今回は、アイリス(iris, アヤメ)のデータを使いましょう。
1 | iris = dataset("datasets","iris") |
150 rows × 5 columns
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species | |
|---|---|---|---|---|---|
| Float64 | Float64 | Float64 | Float64 | Cat… | |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
この表形式のデータは、DataFrame(データフレーム)と呼ばれる型で、2次元の配列(行列)のように操作できますが、特有の操作も持っています。
iris以外にも、たくさんのデータセットがあります:Available datasets – Rdatasets
第1列、SepalLength(がく片の長さ)をデータ(ベクトル)として取り出しましょう。
1 | SepalLength = iris[:,1] |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 150-element Vector{Float64}: 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 ⋮ 6.0 6.9 6.7 6.9 5.8 6.8 6.7 6.7 6.3 6.5 6.2 5.9 |
150成分のデータがあります。この全体像を知るには、データの階級ごとの頻度を図示した、ヒストグラム(histogram)を使うのが手っ取り早いです。
「histogram(データ)」でヒストグラムが描けます。binsによって、ビン(棒)の個数を指定できます。
1 | histogram(SepalLength,bins =30) |
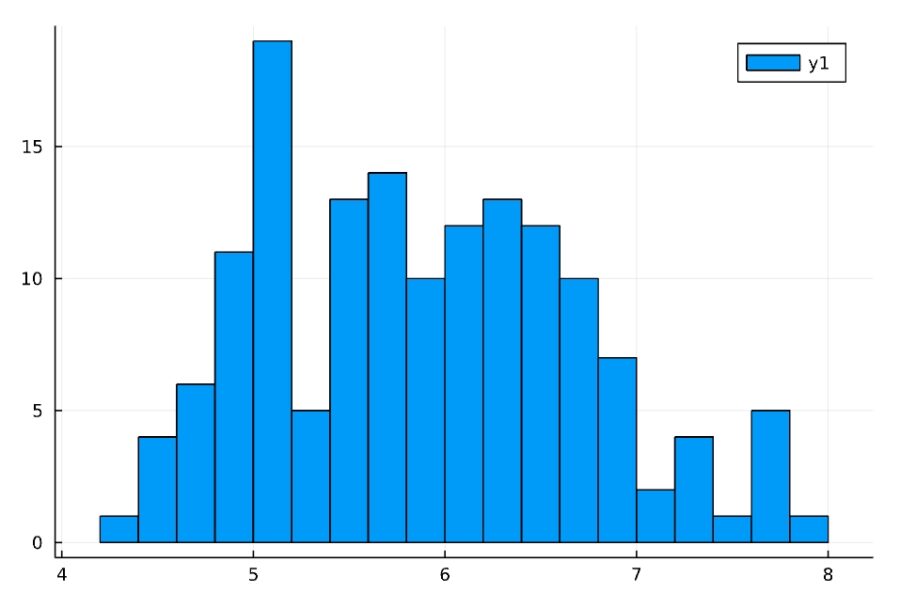
花弁の長さ(PetalLength)を、同様にプロットしてみましょう。
1 2 | PetalLength = iris[:,3] histogram(PetalLength, bins=30) |

ばらつきがあるのがわかりますね。
このばらつきは、アイリスの中でも品種による違いが大きく表れたものです。
データフレームの第5行にはSpecies(品種)の情報がありますが、さきほどの簡略表示では「setosa」しか見えませんでした。
カテゴリ分けされたデータの名前、値の種類を取り出すには、「levels(データ)」です。
1 | levels(iris[:,5]) |
1 2 3 4 | 3-element Vector{String}: "setosa" "versicolor" "virginica" |
「@df データフレーム histogram(:列名, group=:分類列)」で、分類列に応じてヒストグラムを描くことができます。
1 | @df iris histogram(:PetalLength, group=:Species) |
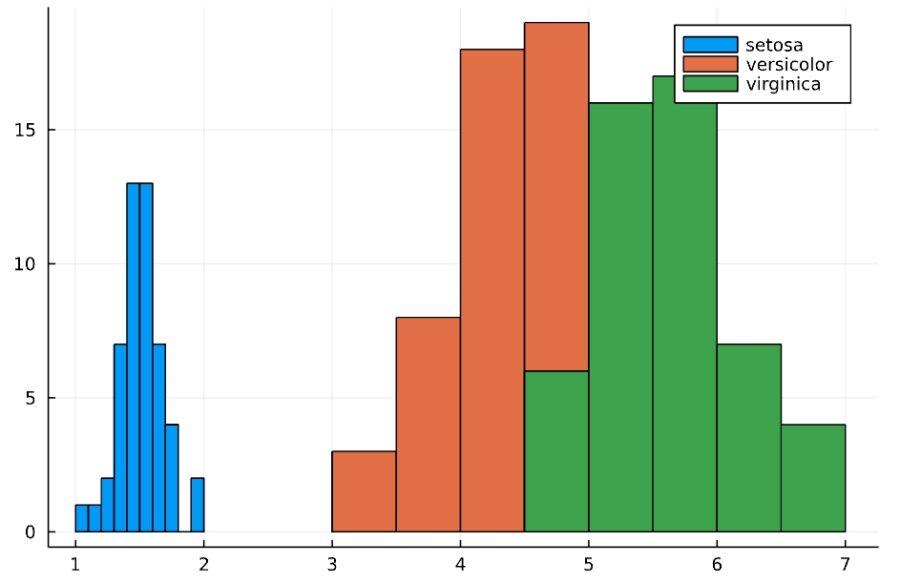
品種による違いが明確になりました。
データの箱ひげ図を描く
データをその大きさ順に並び替えたときのようすを説明する箱ひげ図(box plot)を描くには、「boxplot(データ)」です。
1 | boxplot(SepalLength) |
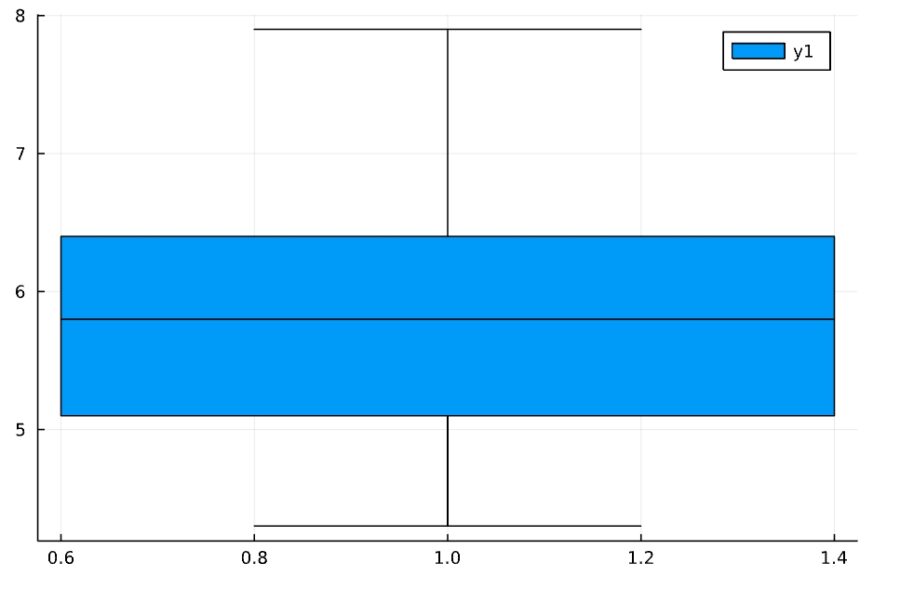
上下にある横線が、データの範囲(range)を示しています。上側が最大値、下側が最小値です。
箱(色塗られた長方形)に含まれる部分に、全体の50%個のデータがあります。箱の下側が全体の25%:第1四分位数\(Q_1\)、真ん中が50%(中央値 median)\(Q_2\)、上側が75%:第3四分位数\(Q_3\)です。
箱の範囲\(Q_3 -Q_1\)を、四分位範囲(IQR; interquartile range)と呼びます。
品種による違いを見るために、品種ごとに箱ひげ図を描いてみましょう。
「groupby(データフレーム, グループ分けに使う列)」で、データフレームをそのグループ毎に分けることができます。
1 | iris_group=groupby(iris, :Species) |
1 2 3 4 | GroupedDataFrame with 3 groups based on key: Species First Group (50 rows): Species = CategoricalArrays.CategoricalValue{String, UInt8} "setosa" ⋮ Last Group (50 rows): Species = CategoricalArrays.CategoricalValue{String, UInt8} "virginica" |
例えば、その3番目は品種virginica(バージニカ)のみを集めたデータフレームです。
1 | iris_group[3] |
50 rows × 5 columns
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species | |
|---|---|---|---|---|---|
| Float64 | Float64 | Float64 | Float64 | Cat… | |
| 1 | 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 2 | 5.8 | 2.7 | 5.1 | 1.9 | virginica |
| 3 | 7.1 | 3.0 | 5.9 | 2.1 | virginica |
| 4 | 6.3 | 2.9 | 5.6 | 1.8 | virginica |
| 5 | 6.5 | 3.0 | 5.8 | 2.2 | virginica |
この情報を使って、各品種の花弁の長さのデータの箱ひげ図をプロットしましょう。
1 2 3 | boxplot(iris_group[1][:,5],iris_group[1][:,3]) boxplot!(iris_group[2][:,3]) boxplot!(iris_group[3][:,3]) |
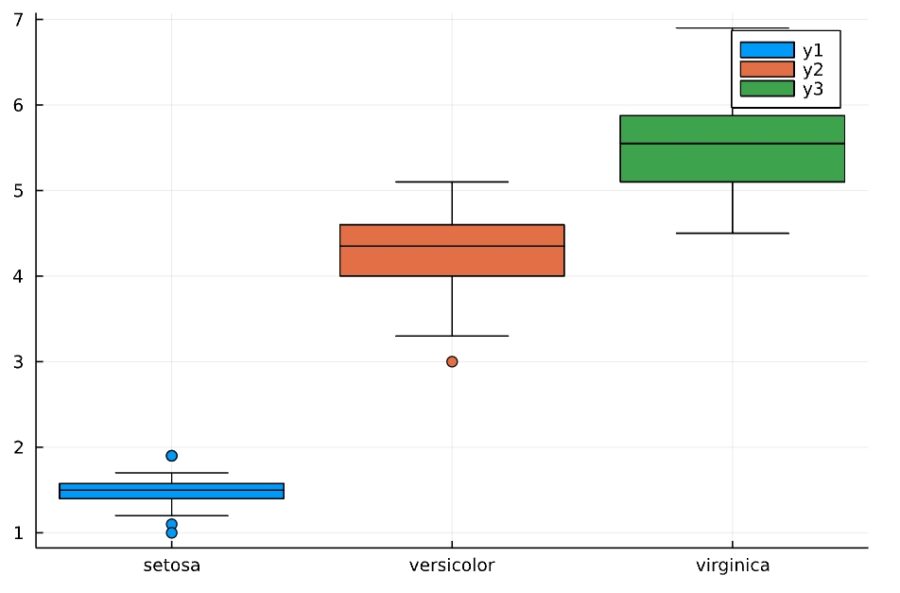
丸(ドット)で示されているのは、外れ値(outlier)です。デフォルトでは、箱から四分位範囲×1.5以上の外側が外れ値として扱われています。
したがって、上下のひげは、(外れ値を取り除いたあとでの)最大値、最小値を表しています。
平均、中央値、分散を求める方法
データを図示して全体像を見てきたので、続いては数値的にデータを分析しましょう。
データフレームの概要を知るには、「describe(データ)」が便利です。
1 | describe(iris) |
5 rows × 7 columns
| variable | mean | min | median | max | nmissing | eltype | |
|---|---|---|---|---|---|---|---|
| Symbol | Union… | Any | Union… | Any | Int64 | DataType | |
| 1 | SepalLength | 5.84333 | 4.3 | 5.8 | 7.9 | 0 | Float64 |
| 2 | SepalWidth | 3.05733 | 2.0 | 3.0 | 4.4 | 0 | Float64 |
| 3 | PetalLength | 3.758 | 1.0 | 4.35 | 6.9 | 0 | Float64 |
| 4 | PetalWidth | 1.19933 | 0.1 | 1.3 | 2.5 | 0 | Float64 |
| 5 | Species | setosa | virginica | 0 | CategoricalValue{String, UInt8} |
meanが平均値、minが最小値、medianが中央値、maxが最大値を表しています。
品種ごとに平均値や中央値を見ると、その違いが数値的にわかりやすいです。
1 2 3 | for i in 1:3 display(describe(iris_group[i])) end |
個別のデータに対し、平均値、最小値、中央値、最大値は次のような関数で計算できます。
1 2 3 4 | mean(iris[:,1]) minimum(iris[:,1]) median(iris[:,1]) maximum(iris[:,1]) |
1 2 3 4 | 5.843333333333334 4.3 5.8 7.9 |
\[\mathrm{mean}(x) := \frac{1} {n} \sum_{i=1} ^n x_i\]
分散と標準偏差は、「var(データ)」「std(データ)」で計算できます。
1 2 | var(iris[:,1]) std(iris[:,1]) |
1 2 | 0.6856935123042507 0.828066127977863 |
ここで計算される分散は、分母が\(n-1\)の不偏分散(unbiased variance)です。
\[\mathrm{var}(x) := \frac{1} {n-1} \sum_{i=1} ^n (x_i – \mathrm{mean}(x))^2\]
\[\mathrm{std}(x) := \sqrt{\mathrm{var}(x) }\]
品種グループごとに、がく片の長さのデータの分散を求めてみましょう。
1 2 3 | for i in 1:3 println(iris_group[i][1,5]," ",var(iris_group[i][:,1])) end |
1 2 3 | setosa 0.12424897959183674 versicolor 0.2664326530612245 virginica 0.4043428571428572 |
全体の分散(約0.69)と比べると、グループごとの方が分散が小さくなっていますね。その中でも、setosaは分散が比較的小さく、virginicaは分散が比較的大きいことがわかりました。
以上、Juliaでデータのヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法を紹介してきました。
データを図と数値の両面から理解するのは大事です。今回の説明が、Juliaでデータ・統計分析するのに役立てば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう