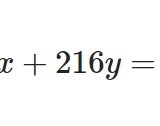どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で1変数関数の最大値最小値を求める方法を紹介します。
準備
SymPy, Plotsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("SymPy") Pkg.add("Plots") |
準備として、以下のコードを実行しておきます。
1 | using SymPy, Plots |
1変数関数の最大値最小値を求める方法
まず、変数として用いる記号を用意しておきましょう。
1 | @syms x |
関数の最大値は、「sympy.maximum(関数,x ,sympy.Interval(範囲))」で求められます。最小値は「minimum」です。
1 2 | sympy.maximum(x^2 - 2*x + 1,x ,sympy.Interval(2,3)) sympy.minimum(x^2 - 2*x + 1,x ,sympy.Interval(2,3)) |
\[ \begin{aligned}4\end{aligned} \]
\[ \begin{aligned}1\end{aligned} \]
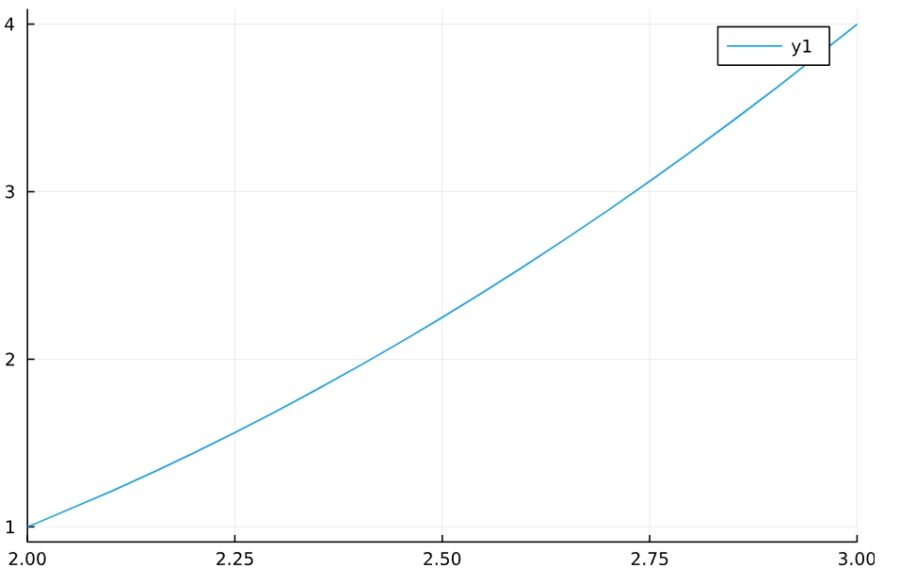
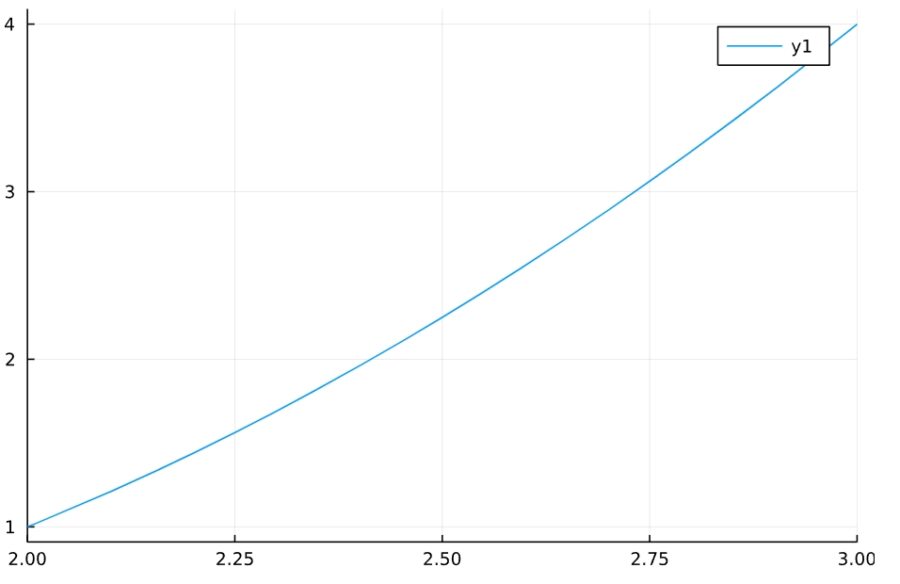
この結果が正しいことは、そのグラフからも読み取れます。
1 | plot(x^2 - 2*x + 1, xlims=(2,3)) |
最大値を使って、最大値を取る点(最大点)を求めてみましょう。まず、最大点の方程式は
1 | Eq(x^2 - 2*x + 1,sympy.maximum(x^2 - 2*x + 1,x ,sympy.Interval(2,3))) |
\[ \begin{aligned}x^{2} – 2 x + 1 = 4\end{aligned} \]
と表せます。これを「solveset(方程式,x, 区間)」で解けば、
1 | solveset(Eq(x^2 - 2*x + 1,sympy.maximum(x^2 - 2*x + 1,x ,sympy.Interval(2,3))) , x, sympy.Interval(2,3) ) |
\[ \begin{aligned}\left\{3\right\}\end{aligned} \]
と、\(x=3\)で最大値\(4\)を取ることがわかります。最小点についても同様です。
1 | solveset(Eq(x^2 - 2*x + 1,sympy.minimum(x^2 - 2*x + 1,x ,sympy.Interval(2,3))) , x, sympy.Interval(2,3) ) |
\[ \begin{aligned}\left\{2\right\}\end{aligned} \]
関数の定義域は有界(有限)とは限らなくても求められます。2つのオー「oo」がSymPyにおいて\(\infty\)を表します。「sympy.Interval(-oo,oo)」が実数全体\(\mathbb{R} = (-\infty ,\infty)\)です。
1 2 | sympy.maximum(x^2 - 2*x + 1,x ,sympy.Interval(-oo,oo)) sympy.minimum(x^2 - 2*x + 1,x ,sympy.Interval(-oo,oo)) |
\[ \begin{aligned}\infty\end{aligned} \]
\[ \begin{aligned}0\end{aligned} \]
ただし、プロットの範囲で「oo」を用いるとエラーが出てしまいます。
1 | plot(x^2 - 2*x + 1, xlims=(-oo,oo)) |
1 | ArgumentError: start and stop must be finite, got -Inf and Inf |
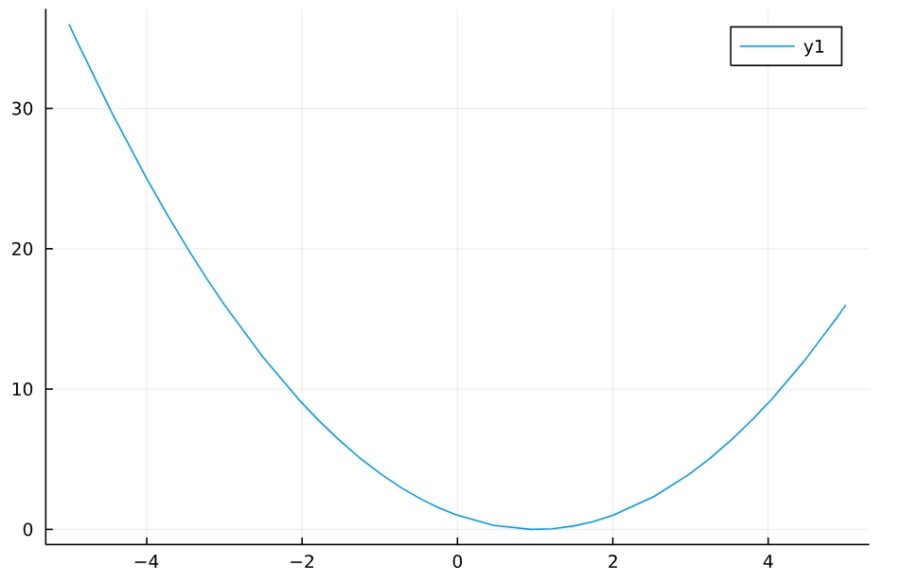
これを回避するには、範囲指定なしで描けば良いでしょう。
1 | plot(x^2 - 2*x + 1 ) |
以上の結果をまとめて、与えられた範囲における関数の最大点、最大値、最小点、最小値を求め、グラフを描く関数を作ってみましょう。
端点が無限大ooを含むかどうかによって、グラフの描き方を変えています。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | function maxmin(f,a,b) max_v = sympy.maximum(f,x ,sympy.Interval(a,b)) min_v = sympy.minimum(f,x ,sympy.Interval(a,b)) max_p = solveset(Eq(f,max_v) , x, sympy.Interval(a,b)) min_p = solveset(Eq(f,min_v) , x, sympy.Interval(a,b)) println("最大点 ",max_p) println("最大値 ",max_v) println("最小点 ",min_p) println("最小値 ",min_v) if a == -oo || b== oo plot(f, label="f") else plot(f, xlims =(a,b) , label="f") end end |
これを使えば、今までの結果が簡単に得られます。
1 | maxmin(x^2-2*x +1 ,2,3) |
1 2 3 4 | 最大点 {3} 最大値 4 最小点 {2} 最小値 1 |
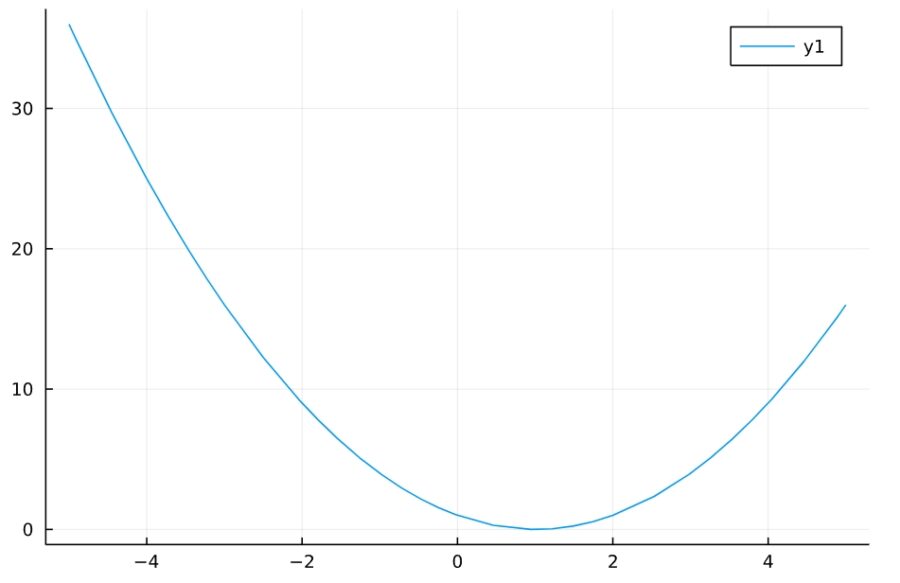
1 | maxmin(x^2-2*x +1 ,-oo,oo) |
1 2 3 4 | 最大点 EmptySet 最大値 oo 最小点 {1} 最小値 0 |
3次関数についても、問題なく計算できます。
1 | maxmin(x^3 - 6x^2 + 11x - 6 ,2,3) |
1 2 3 4 | 最大点 {2, 3} 最大値 0 最小点 {sqrt(3)/3 + 2} 最小値 -6*(sqrt(3)/3 + 2)^2 + 11*sqrt(3)/3 + 16 + (sqrt(3)/3 + 2)^3 |

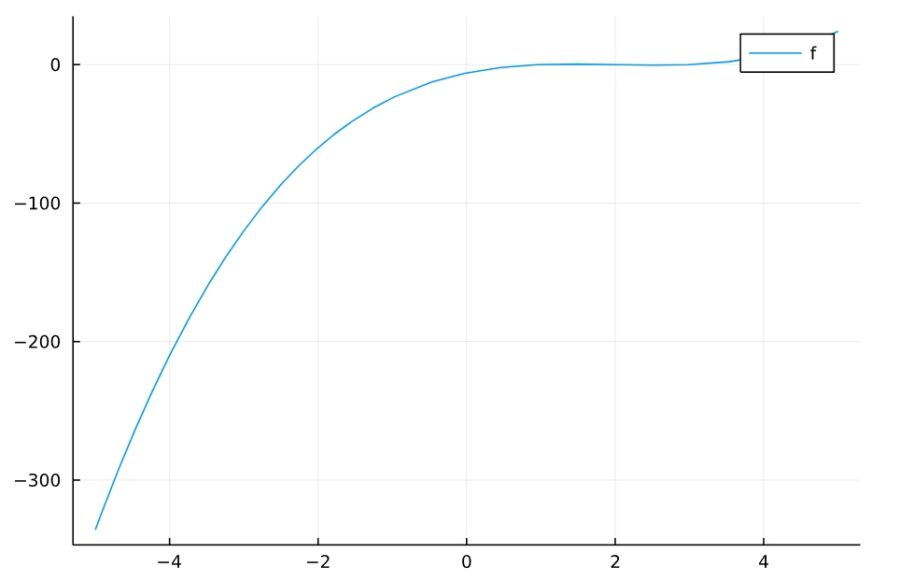
1 | maxmin(x^3 - 6x^2 + 11x - 6 ,-oo,0) |
1 2 3 4 | 最大点 {0} 最大値 -6 最小点 EmptySet 最小値 -oo |
指数関数や対数関数でも可能です。
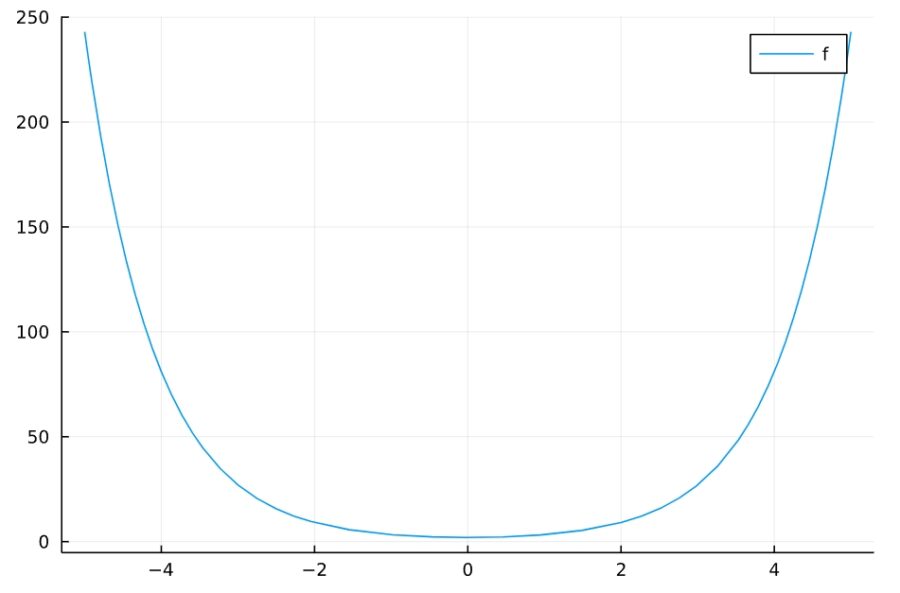
1 | maxmin(3^x +3^(-x) ,-oo,oo) |
1 2 3 4 | 最大点 EmptySet 最大値 oo 最小点 {0} 最小値 2 |
1 | maxmin(log(x)*log(x^2) ,1,3) |
1 2 3 4 | 最大点 ConditionSet(x, Eq(log(x)*log(x^2) - log(3)*log(9), 0), Interval(1, 3)) 最大値 log(3)*log(9) 最小点 {1} 最小値 0 |
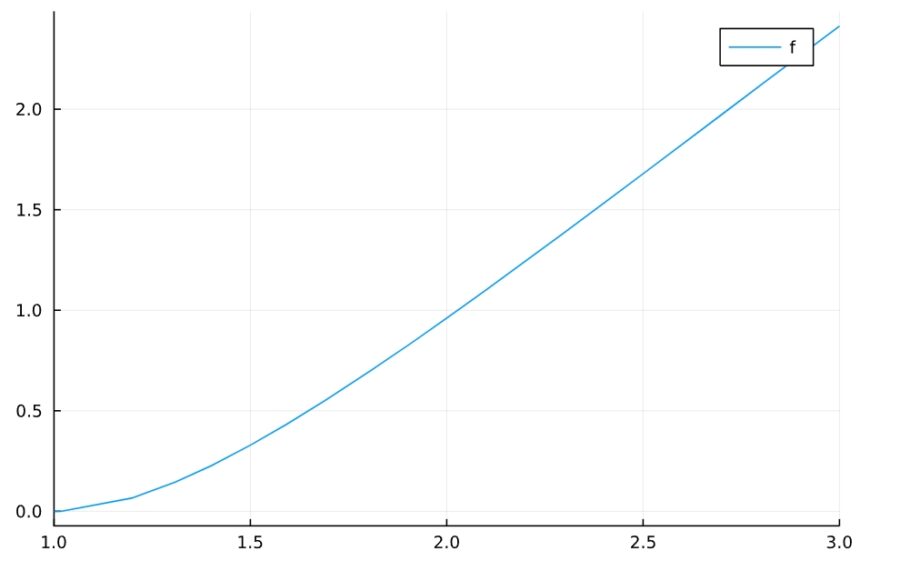
対数関数の例では、最大点の計算がうまくできていませんね。
有理関数の場合は、計算する範囲によって、うまく求められたり、求められなかったりします。
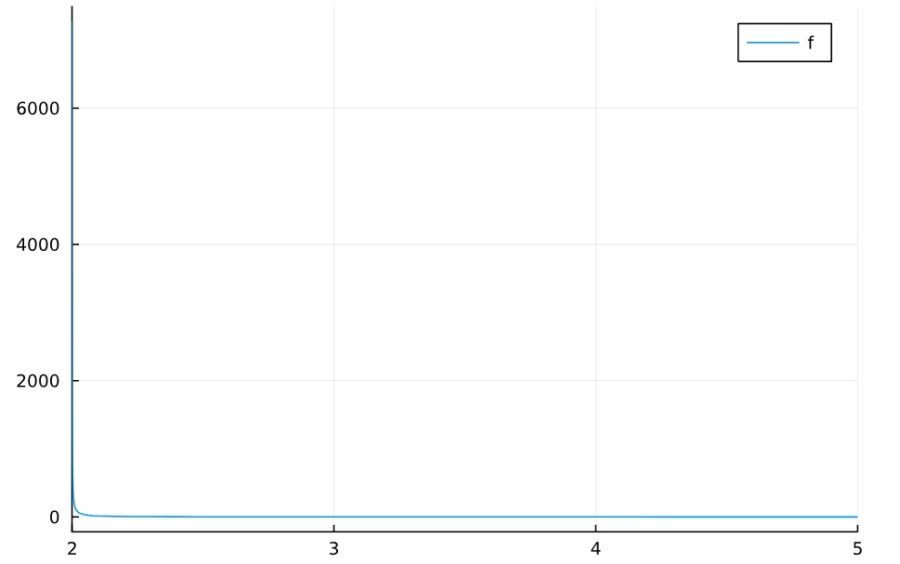
1 | maxmin((2x+1)/((x-2)*(x-1)*(x+1)) ,2,5) |
1 2 3 4 | 最大点 EmptySet 最大値 oo 最小点 {5} 最小値 11/72 |
1 | maxmin((2x+1)/((x-2)*(x-1)*(x+1)) ,-1//10,1//10) |
1 2 3 4 | 最大点 EmptySet 最大値 0.637958532695375 最小点 {-0.1} 最小値 0.384800384800385 |
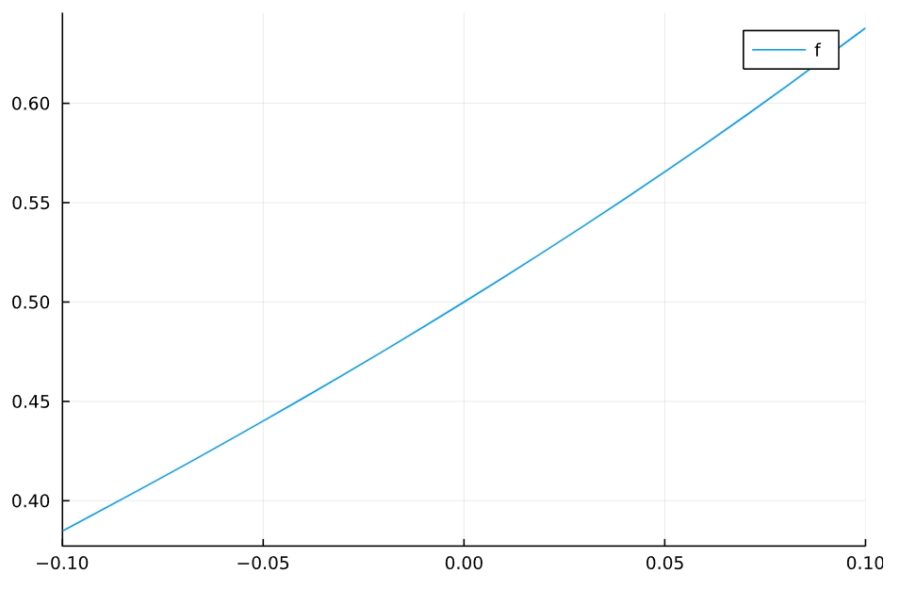
この例では、最大値が存在するのに、最大点が存在しないことになってしまっています。
1 | sympy.maximum((2x+1)/((x-2)*(x-1)*(x+1)),x ,sympy.Interval(-1//10,1//10)) |
\[ \begin{aligned}0.637958532695375\end{aligned} \]
最大値が代数的にきれいに解けず、数値的に求められているので、誤差によって最大点の方程式の解がなくなってしまうのでしょう。
また、範囲によっては時間がかかりすぎて、結果が得られません。
1 | maxmin((2x+1)/((x-2)*(x-1)*(x+1)) ,1,2) |
特殊関数、例えばガンマ関数の最大値、最小値を求めることもできません。
1 2 | sympy.gamma(x) maxmin(sympy.gamma(x) ,1,3) |
\[ \begin{aligned}\Gamma\left(x\right)\end{aligned} \]
1 | NotImplementedError('Unable to find critical points for gamma(x)') |
勾配降下法を使えば、極小値を数値的に求めることはできます。
参考:勾配降下法(Python)でガンマ関数の極小値を調べてみよう
以上、Julia(SymPy)で1変数関数の最大値最小値を求める方法を紹介してきました。
限界はありますが、ある程度の問題ならば最大点、最小点も合わせて素早く求めてくれるので、便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(SymPy)で多項式の展開・因数分解、方程式を解く方法
Juliaで1変数関数のグラフを描く方法(多項式、指数対数、三角関数)
勾配降下法(Python)でガンマ関数の極小値を調べてみよう