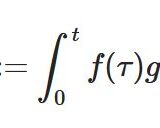どうも、木村(@kimu3_slime)です。
今回は、ヴォルテラの積分方程式とは何か、そのラプラス変換による解き方を紹介します。
ヴォルテラの積分方程式
積分方程式(integral equation)とは、
\[ \begin{aligned}y(x)+\int _0^x y(\tau)(x-\tau)d\tau =x\end{aligned} \]
といった未知関数\(y\)に関する積分を含む方程式です。
一般に、
\[ \begin{aligned}y(x)=\lambda \int _0^x K(x,\tau )y(x)d\tau +f(\tau)\end{aligned} \]
と表される方程式は、(第二種)ヴォルテラの積分方程式(Volterra integral equation of the second kind)と呼ばれています。ここで積分内に登場する関数\(K(x,\tau)\)は積分核(integral kernel)と呼ばれるものです。
積分の端点が変数なものはヴォルテラの積分方程式、固定されているものはフレドホルムの積分方程式と分類されています。
第二種のヴォルテラ積分方程式は、例えば波動方程式を解く中で登場します。
ラプラス変換による解き方
一般には、積分方程式を解くためには級数解法が有効です。
ただし、簡単な問題ならば、ラプラス変換を使って明示的に解くことができます。
\[ \begin{aligned}y(x)+\int _0^x y(\tau)(x-\tau)d\tau =x\end{aligned} \]
という積分方程式を、ラプラス変換によって解いてみましょう。
積分の部分は\(y\)と\(f(x)=x\)の畳み込みの形になっているため、
\[ \begin{aligned}y(x)+(y*f)(x) =x\end{aligned} \]
となります。両辺をラプラス変換しましょう。畳み込みの性質\(L(f*g)=L(f)L(g)\)、\(L(x)=\frac{1}{s^2}\)に注意して、
\[ \begin{aligned}L(y)+L(y)\frac{1}{s^2}=\frac{1}{s^2}\end{aligned} \]
\[ \begin{aligned}L(y)= \frac{1}{s^2+1}\end{aligned} \]
となります。\(L(\frac{1}{\omega} \sin \omega x) = \frac{1}{s^2+\omega^2}\)を使って逆ラプラス変換すれば、
\[ \begin{aligned}y(x)= \sin x\end{aligned} \]
と解を求めることができました。
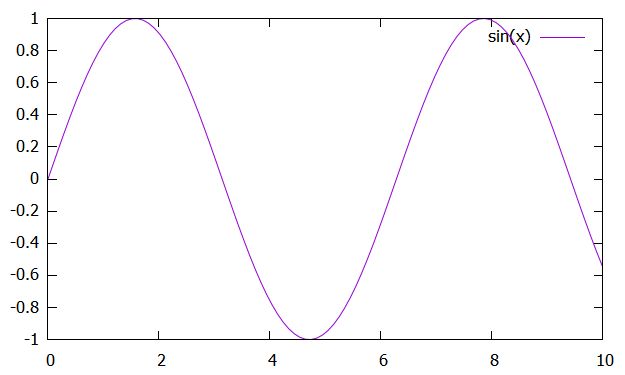
この結果を少し一般化すれば、
\[ \begin{aligned}y(x)+\omega ^2\int _0^x y(\tau)(x-\tau)d\tau =\omega x\end{aligned} \]
の解が
\[ \begin{aligned}y(x) = \sin \omega x\end{aligned} \]
であることがわかりますね。
以上、ヴォルテラの積分方程式とは何か、そのラプラス変換による解き方を紹介しました。
積分核\(K(x,\tau)\)が\(K(x-\tau)\)という形をしているときは、積分が畳み込みの形で表せるので、ラプラス変換によって計算できます。ラプラス変換の応用として、この手の積分方程式が解けると知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)