どうも、木村(@kimu3_slime)です。
今回は、ニュートンの冷却法則について、その意味と解き方を紹介します。
ニュートンの冷却法則
熱したフライパンの冷却について考えてみましょう。時間が経てば、やがて外気温まで冷めていくことでしょう。そのとき、温度差が大きいほど熱は速く冷めることが経験的に知られています。さらに、単にそのまま放置して冷やすか、風を送るか、水につけるか、また物質の種類によって、冷めるまでの速度も違うはずです。
このような性質を説明する法則が、ニュートンの冷却法則(Newton’s law of cooling)と呼ばれる微分方程式です。
\[ \begin{aligned}\frac{dT}{dt}= -k (T-T_{s})\end{aligned} \]
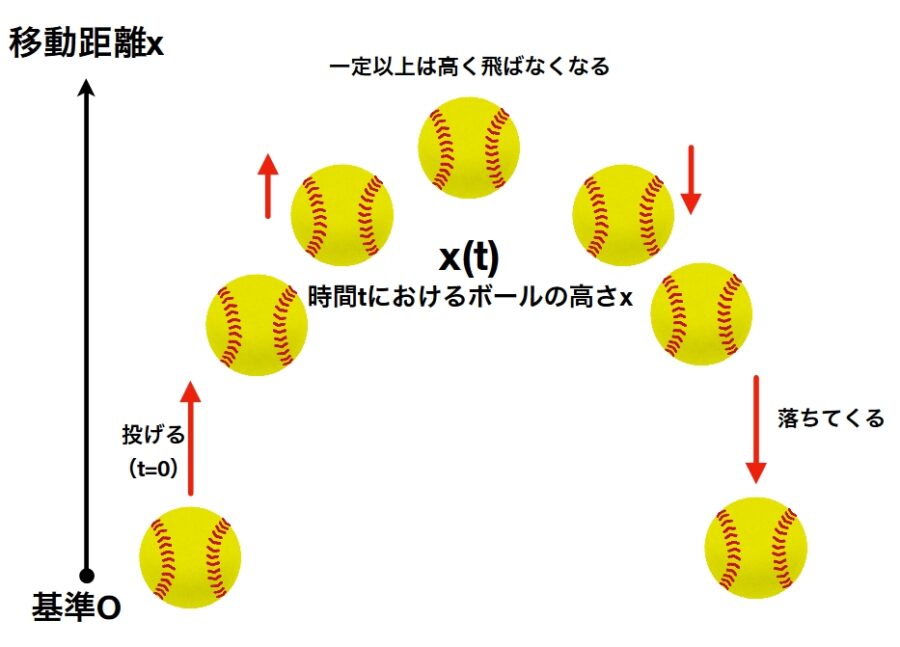
\(T\)は熱した物質の温度で、時間\(t\)を変数とする関数\(T(t)\)として考えます。\(T_{s}\)は周囲の環境の温度で、定数です。\(k>0\)は、冷却の強さを表す定数(熱伝達率)です(熱容量、表面積、熱伝導率などに依存)。
数式の読み方としては、次のようになります。\(\frac{dT}{dt}\)は温度の時間変化率で、それが右辺に等しいと言っています。\(T-T_{s}\)は物体と環境の温度差で、それに比例して冷えていくと。比例定数\(k\)が大きくなるほど、\(\frac{dT}{dt}\)は大きくマイナスになり、すぐに冷えていくわけです。
では、微分方程式を解いてみましょう。これは変数分離形と呼ばれる形です。
両辺を\(T-T_{s}\)で割ると、
\[ \begin{aligned} \frac{\frac{dT}{dt}}{ T-T_{s}} = -k\end{aligned} \]
となり、これを\(t\)について積分すれば、
\[ \begin{aligned}\int \frac{1}{T-T_s} dT = \int -k dt\end{aligned} \]
です。積分を計算すると、
\[ \begin{aligned}\log (T-T_s)= -kt +C\end{aligned} \]
(\(C\)は積分定数)なので、両辺の指数関数を取れば
\[ \begin{aligned}T-T_s = e^{-kt +C}\end{aligned} \]
で、
\[ \begin{aligned}T= e^C e^{-kt}+T_s \end{aligned} \]
となりました。特に初期値を\(T(0)=T_0\)とすると、
\[ \begin{aligned}T(t)= (T_0-T_s)e^{-kt}+T_s\end{aligned} \]
と表せます。これが微分方程式の解です。
そもそも\(T_0 = T_s\)のときは温度は一定であること、\(T_0 -T_s\)、\(k\)が大きいほど冷却が速くなることが数式の上でも読み取れますね。

この式を使って計算してみましょう。
フライパンを冷ますとき、\(T_0 =100\)で、\(T_s =20\)だったとします。\(t=30\)のとき\(T(t)=50\)のとき、ニュートンの冷却法則における\(k\)はおよそいくつと考えられるでしょうか?
仮定を微分方程式の解に代入します。
\[ \begin{aligned}50 =(100-20)e^{-30k}+20\end{aligned} \]
で、対数を取って整理すれば
\[ \begin{aligned}k = -\frac{1}{30}\log \frac{3}{8}\end{aligned} \]
となります。近似値としては、
\[ \begin{aligned}k \simeq 0.03\end{aligned} \]
と求まりました。
同じ状況で、\(T_0=200\)、\(T_s=0\)とします。\(T(t)= 100\)となる時間\(t\)はいくつでしょうか?
再び微分方程式の解に代入すると、
\[ \begin{aligned}100 =(200-0)e^{-kt}+0\end{aligned} \]
で、対数を取れば
\[ \begin{aligned}t= -\frac{1}{k} \log \frac{1}{2}\end{aligned} \]
で、さきほどの結果を使えば
\[ \begin{aligned}t= \frac{30}{\log \frac{3}{8}}\log \frac{1}{2}\end{aligned} \]
です。近似値としては、
\[ \begin{aligned}t\simeq 21.2\end{aligned} \]
であることがわかりました。
この例のような計算をすれば、\(k\)を推定できて、それをもとに冷却のようすをシミュレーションできることがわかりますね。
以上、ニュートンの冷却法則、その意味と解き方を紹介してきました。
おおざっぱな近似式ですが、簡単なので数学的に扱いやすいのが良いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)