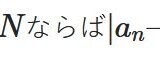どうも、木村(@kimu3_slime)です。
今回は、積分の絶対値に関する三角不等式
\[ \begin{aligned}|\int _a ^b f(x)dx| \leq \int _a ^b |f(x)|dx\end{aligned} \]
について紹介します。
積分の三角不等式とは
積分の三角不等式は、積分の線形性や単調性と合わせて、積分に関する基本的な性質です。高校数学ならば、証明なしに用いて良いでしょう。
もし\(f\)が非負(正)の値を取るならば、不等式には等号が成り立っています。例ですが、
\[ \begin{aligned} |\int_0^1 x dx|&= \int _0^1 |x|dx \\ &= \int _0^1 x dx \\ &= \frac{1}{2} \end{aligned} \]
となるので。関数の値が常に正である限り、絶対値を取っても何も変わりませんね。
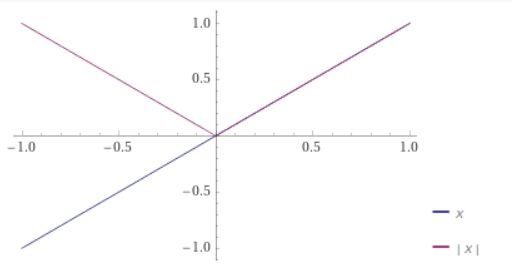
ただし、\(f\)の符号が正負混ざっていると、状況が変わってきます。次の例を見てください。
\[ \begin{aligned}|\int_{-1} ^1 x dx| =|[\frac{1}{2}x^2]_{-1}^1 |= 0\end{aligned} \]
\[ \begin{aligned} \int _{-1} ^1 |x| dx &=\int _{-1}^0 -xdx+\int_0^1 x dx \\&= [-\frac{1}{2}x^2]_{-1}^0+ [\frac{1}{2}x^2]_{0}^1 \\ &= 1\end{aligned} \]
確かに、三角不等式
\[ \begin{aligned}0=|\int_{-1} ^1 x dx| \leq \int _{-1} ^1 |x| dx =1\end{aligned} \]
は成り立っていますね。左辺は符号付きの面積を計算し、絶対値を取ったものです。右辺は関数が負の値を取る部分を折り返し、面積を計算したものです。
左辺では、この例のように正負の面積が打ち消し合う現象が起こりえますが、右辺ではそれは起こりえませんね。そのことを表しているのが三角不等式です。
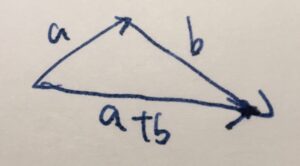
なぜ、三角不等式という名前なのでしょうか。それはベクトルに関する三角不等式に由来しているからでしょう。
\[ \begin{aligned}|a+b| \leq |a|+|b|\end{aligned} \]
\[ \begin{aligned}\|a+b\|\leq \|a\| +\|b\|\end{aligned} \]
といった不等式は、三角不等式と呼ばれるものです。
絶対値に関する三角不等式を繰り返し用いれば、
\[ \begin{aligned}|\sum_{k=1}^n a_k| \leq \sum_{k=1}^n |a_k|\end{aligned} \]
\[ \begin{aligned}|\sum_{k=1}^\infty a_k| \leq \sum_{k=1}^\infty |a_k|\end{aligned} \]
といった和に関する式が導かれますが、\(\sum \to \int\)、\(a_k \to f(x)\)と置き換えた形が
\[ \begin{aligned}|\int _a ^b f(x)dx| \leq \int _a ^b |f(x)|dx\end{aligned} \]
となるので、これは積分の絶対値に関する三角不等式と呼ばれます。積分もある種の和の極限なので、この不等式は成り立ちそうですね。
(紛らわしいのですが、積分のpノルム\(\|f\|_p :=(\int |f(x)|^p dx)^\frac{1}{p}\)に関して、\(\|f+g\|_p \leq \|f\|_p +\|g\|_p\)という形の三角不等式も成り立ちます。こちらはミンコフスキーの不等式と呼ばれることが多いです。)
積分の三角不等式の証明
では、積分の三角不等式を証明しましょう。
今回は、\(f\)を有界な区間\([a,b]\)上の連続関数として示します。\(f,|f|\)はともに連続関数であり、したがって積分可能です。
積分の一般的な性質として、関数に関する単調性があります。\( a\leq x \leq b\)を満たすすべての\(x\)の対し\(f(x) \leq g(x)\)が成り立つならば、\(\int_a^b f(x) dx \leq \int _a^b g(x)dx\)が成り立ちます。
これを利用しましょう。絶対値の性質から、すべての\(x\in[a,b]\)に対し、\(-|f(x)| \leq f(x) \leq |f(x)|\)です。したがって、積分の単調性から
\[ \begin{aligned}\int_a^b -|f(x)|dx \leq \int_a^b f(x)dx\leq\int_a^b |f(x)|dx\end{aligned} \]
が成り立ちます。左辺は積分の線形性から\(-\int_a^b |f(x)|dx\)に等しいので、不等式をまとめれば\(|\int _a^ b f(x) dx| \leq \int_a^b |f(x)|dx\)が得られました。
今回は連続関数、1次元の区間に限って示しました。しかし、一般のケース、有界で可積分な関数、重積分(多変数の積分)、複素積分、ルベーグ積分についても同様の不等式が成り立ちます。
積分の定義に戻り、絶対値に関する三角不等式を使って示せます。詳しくは、杉浦「解析入門 Ⅰ」や吉田「ルベーグ積分入門」を参照。
以上、積分の絶対値に関する三角不等式を紹介してきました。
積分の大きさ(絶対値)を評価するときには、すぐに使える簡単な不等式です。ぜひ安心して使ってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)
日本評論社 (2021-03-15T00:00:00.000Z)
¥3,960
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは
不等式の証明で等号成立を確かめる必要がないのはなぜか:≦の意味