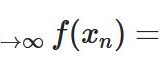どうも、木村(@kimu3_slime)です。
高校・大学の数学・微積分では、\(f(x)/x\)の形の極限の公式
\[ \begin{aligned}\lim_{x \to 0}\frac{\sin x}{x} =1\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{\cos x -1}{x} =0\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{e^x -1}{x} =1\end{aligned} \]
\[ \begin{aligned}\lim_{x \to 0}\frac{\log _e (1+x)}{x} =1\end{aligned} \]
を覚えておくと、極限の計算がしやすいです。今回は、これらの有名な極限の公式の覚え方を紹介します。
極限の公式の意味
どの公式も\(\lim_{x \to 0}\frac{f(x)}{x}\)という形をしていますが、その意味を知ると覚えやすいです。
それは、単純な一次関数\(g(x)=x\)と少し複雑な関数\(f(x)\)を原点\(x=0\)付近で比較しているということです。具体的には、分子の関数と分母の1次関数をグラフに書いて比べてみると良いでしょう。

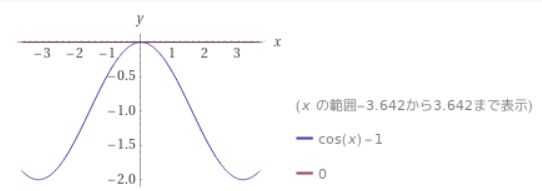
画像引用:cos x – 1, 0x – Wolframalpha
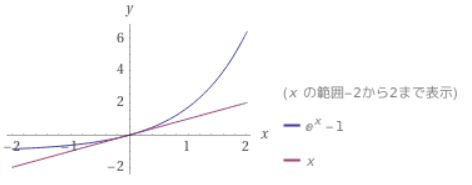
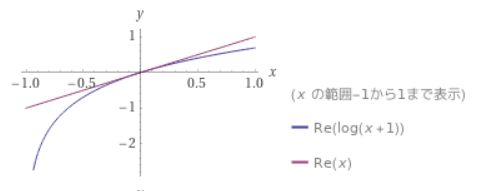
画像引用:log_e (1+x),x – Wolframalpha
どの直線も、分子の関数\(f(x)\)を原点付近でよく近似していますね。
これらの公式は
\[ \begin{aligned}\lim _{x \to 0}\frac{f(x)-f(0)}{x}=a\end{aligned} \]
という形なので、これを\(x=0\)での微分の定義\(\lim _{x \to 0} \frac{f(x)-f(0)}{x-0} = f^\prime (0)\)として見れば、
\[ \begin{aligned}f^\prime (0)=a\end{aligned} \]
を意味します。これは、分子の関数\(f(x)\)の原点での接線の傾きが\(a\)である、原点付近では直線\(g(x)=ax\)によって近似される、ということですね。
この発想を逆に取って、三角関数(サイン、コサイン)、指数関数、対数関数を\(x=0\)において近似する直線を考えれば、これらの極限の公式は当たり前のような事実として認識できるでしょう。
分子に\(-1\)がついたりするのは\(f(0)\)での\(y\)軸方向のずれを修正するもので、対数関数で\(\log _e x\)でなく\(\log_e (x+1)\)を考えるのは\(\log _e 0\)は存在せず\(\log _e 1 =0\)付近をが近似しやすいからです。\(x=1\)付近で対数関数を見るならば、
\[ \begin{aligned}\lim_{x \to 1}\frac{\log _e x}{x-1} =1\end{aligned} \]
となります。
テイラー展開による説明
これらの公式は、初等関数のテイラー展開というものを知るとより覚えやすいでしょう。
テイラー展開とは、何回も微分できる関数\(f(x)\)は\(x=a\)の付近で
\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots\end{aligned} \]
と多項式の和として展開・近似できるという定理です。
例えば、サインならば
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots\end{aligned} \]
と近似できます。
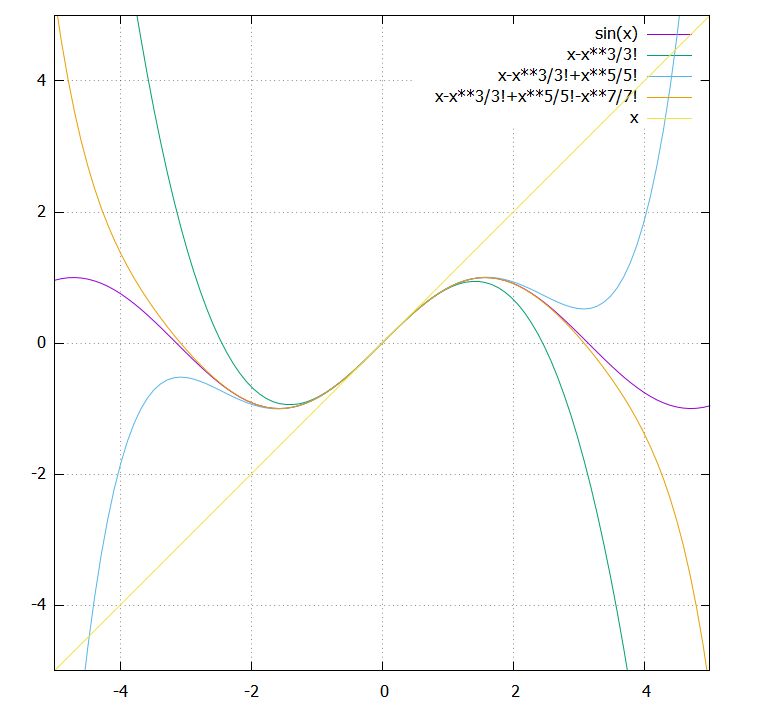
三角関数、指数関数、対数関数のような初等関数のテイラー展開は、ごく最初の項を覚えておくだけで非常に便利です。一般形を覚えておけば、微分の計算をして求めることもできます。
\[ \begin{aligned} \sin x&=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots \\ &= \sum_{k=0}^\infty \frac{(-1)^{k}}{(2k+1)!}x^{2k+1} \end{aligned} \]
\[ \begin{aligned} \cos x&=1- \frac{x^2}{2!}+ \frac{x^4}{4!}- \cdots \\&= \sum_{k=0}^\infty \frac{(-1)^{k}}{(2k)!}x^{2k} \end{aligned} \]
\[ \begin{aligned} e^x&=1+x+\frac{x^2}{2!}+ \frac{x^3}{3!}+ \cdots \\&=\sum_{k=0}^\infty \frac{1}{k!}x^{k} \end{aligned} \]
\[ \begin{aligned} \log _e (1+x)&=x- \frac{x^2}{2}+\frac{x^3}{3}- \cdots \\&=\sum_{k=1}^\infty \frac{(-1)^{k+1}}{k}x^{k} \end{aligned} \]
原点\(x=0\)におけるテイラー展開は、マクローリン展開という名前が個別についているくらい頻出します。
テイラー展開の原理は、平均値の定理を繰り返し使う、というものです:テイラー展開の展開式の覚え方、導き方、証明
テイラー展開と極限の関係を、簡単かつ精密に表すにはランダウの記号が便利です。例えば\(x=0\)の付近では
\[ \begin{aligned} \sin x&=x- \frac{x^3}{6}+ O(x^4)\end{aligned} \]
\[ \begin{aligned} \cos x&=1- \frac{x^2}{2}+O(x^3)\end{aligned} \]
\[ \begin{aligned} e^x&=1+x+x^2+ O(x^3) \end{aligned} \]
\[ \begin{aligned} \log _e (1+x)&=x- \frac{x^2}{2}+O(x^3)\end{aligned} \]
と表せます。\(O(x^k)\)は、おおざっぱに言えば\(k\)次\(x^k\)以降の項をまとめたものです。
1次の部分まで取り出した近似式
\[ \begin{aligned} \sin x& \simeqx\end{aligned} \]
\[ \begin{aligned} \cos x& \simeq1\end{aligned} \]
\[ \begin{aligned} e^x& \simeq1+x \end{aligned} \]
\[ \begin{aligned} \log _e (1+x)& \simeqx\end{aligned} \]
を関数の1次近似と呼びます。これは\(x\)が\(0\)に十分近いとみなせるときに使えるものです。冒頭に紹介した極限の公式は、この1次近似を表すものでした。この近似は物理や科学全般の近似計算で頻繁に登場します。
もう少し高次の項を使って近似すれば、
\[ \begin{aligned}\lim_{x\to 0} \frac{\sin x -x}{x^3} = -\frac{1}{6}\end{aligned} \]
\[ \begin{aligned}\lim_{x\to 0} \frac{\cos x -1}{x^2} =- \frac{1}{2}\end{aligned} \]
\[ \begin{aligned}\lim_{x\to 0} \frac{e^x -1-x}{x^2} = \frac{1}{2}\end{aligned} \]
\[ \begin{aligned}\lim_{x\to 0} \frac{e^x -1-x-x^2}{x^3} = \frac{1}{6}\end{aligned} \]
\[ \begin{aligned}\lim_{x\to 0} \frac{\log_e (1+x) -x}{x^2} =- \frac{1}{2}\end{aligned} \]
といった公式も導かれますね。これらの公式を、はさみうちの原理を使って誘導つきで証明するのは、大学入試数学でも頻出の問題でしょう。
今回は紹介しなかった重要な極限の公式には、
\[ \begin{aligned}\lim _{x\to 0}(1+x)^{\frac{1}{x}}=e\end{aligned} \]
があります。これはオイラー数(ネイピア数)\(e\)の定義です。その導出には、次の記事が参考になるでしょう。
参考:なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化
以上、有名な極限の公式の覚え方として、接線による近似、テイラー展開について紹介してきました。
\(\lim _{x \to 0} \frac{f(x)}{x}\)という形の極限を見たら、原点付近で分母の関数を1次関数によって近似しようとしているのだな、と思えば、自然に公式は思い出せるようになるでしょう。テイラー展開まで知っておくと、さらに高次の近似式も使いこなせるようになって便利です。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)
こちらもおすすめ
なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化