どうも、木村(@kimu3_slime)です。
今回は、数ベクトルのpノルム、絶対値ノルム、最大値ノルム、とは何か、同値なノルムという考え方も紹介します。
pノルムとは
\(\mathbb{R}^N\)をユークリッド空間(数ベクトル空間)とし、\(x= (x_1,\dots,x_N) \in \mathbb{R}^N\)とします。ベクトルのノルムは
\[ \begin{aligned}\|x\| = (\sum _{i=1}^N x_i ^2)^\frac{1}{2}\end{aligned} \]
というものを考えることが多いでしょう。これをユークリッドノルムと呼ぶのでした。しかし、一般的な意味でのノルムには、さまざまなノルムがあります。
ユークリッドノルムを、次のように一般化してみましょう。\(p\)を\(p>1\)を満たす実数として
\[ \begin{aligned}\|x\|_p := (\sum_{i=1}^N |x_i|^p)^\frac{1}{p}\end{aligned} \]
とします。これを\(p\)ノルム(p-norm)、または\(\ell ^p\)ノルムと呼びます。
この立場からすれば、ユークリッドノルムとは\(2\)ノルムに他なりません。
絶対値ノルム
\(p=1\)のとき、1ノルムは絶対値ノルム(absolute value norm)と呼ばれるものです。
\[ \begin{aligned}\|x\|_1 = \sum_{i=1}^N |x_i| \end{aligned} \]
その名の通り、各成分の絶対値を足し合わせたものと言えます。1次元の絶対値はノルムの一種ですが、それを一般化したノルムです。
例えば、\(\|(1,-1)\|_1 =|1|+|-1|=2\)ですね。
\(p=1,2,3\)のノルムに対して、そのノルムでの単位円\(D_p = \{x \in \mathbb{R}^2 \mid \|x\|_p =1\}\)を描いてみましょう。
\[ \begin{aligned}|x_1|+|x_2|=1\end{aligned} \]
\[ \begin{aligned}x_1^2+ x_2 ^2 =1\end{aligned} \]
\[ \begin{aligned}|x_1|^3+|x_2|^3 =1\end{aligned} \]
例えば\(x_1,x_2>0\)のとき(第一象限)は、\(x_2\)について解けば次のような曲線が得られるとわかるでしょう。
\[ \begin{aligned}x_2 = 1-x_1\end{aligned} \]
\[ \begin{aligned}x_2 = \sqrt{1-x_1^2}\end{aligned} \]
\[ \begin{aligned}x_2 = (1-x_1^3)^\frac{1}{3}\end{aligned} \]
\(p\)ノルムは、各成分をマイナスに置き換えても等しい、各軸について対称なので、次のような図が得られます。
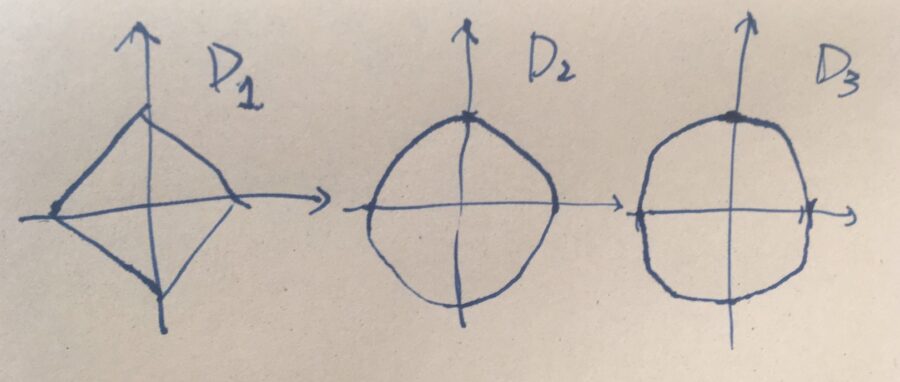
\(D_2\)と\(D_3\)の違いが、図が下手でわかりにくいかもしれません。\(D_1\)より\(D_2\)が外側に膨らんでいるように、\(D_2\)より\(D_3\)は膨らんでいます。
実際、対角線上の点\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} ) \in D_2\)、\((\frac{1}{\sqrt[3]{2}},\frac{1}{\sqrt[3]{2}} ) \in D_3\)を比較するとわかりやすいでしょう。\(\sqrt{2} > \sqrt[3]{2}\)なので、逆数は逆の不等号が成り立ちます。
\(D_1,D_2,D_3\)はどれも「円盤=原点からのノルムが一定の点の集まり」です。円盤といえば普通は\(D_2\)の形を思い浮かべるかも知れませんが、ノルムを変えればさまざまな円盤が考えられます。
絶対値ノルムにより定まる距離
\[ \begin{aligned}d_1(x,y):= \|x-y\|_1\end{aligned} \]
はマンハッタン距離(manhattan distance)と呼ばれます。日本で言えば京都のように、格子や碁盤のように直交した道しか通っていない場所をイメージしましょう。
そこで距離(2点の最短経路)を考えると、斜めに通ることができないので、縦または横の移動量のみを測るのが最短となり、それは各成分の絶対値を足したものとなりますね。
この距離を使った幾何学は、タクシー幾何学(taxicab geometry)と呼ばれるようです。
最大値ノルム
今までは\(p\)は有限値を考えていましたが、その極限的な状況として
\[ \begin{aligned}\|x\|_\infty := \max_{i=1,\dots,N} |x_i|\end{aligned} \]
というノルムを考えます。\(\max\)は右側の対象の最大値を表すものです。
これを最大値ノルム(maximum norm)、無限大ノルム(infinity norm)と呼びます。
最大値ノルムによる円盤\(D_\infty = \{x \in \mathbb{R}^2 \mid \|x\|_\infty =1\}\)はどんな形でしょうか。
ひとつの成分\(x_i\)の絶対値が1になっていたら、\(\|x\|_\infty =1\)です。どちらの成分の絶対値も1になっていなかったら、例えば\(\|(\frac{1}{2}, \frac{1}{2})\|= \frac{1}{2} \neq 1\)です。したがって、
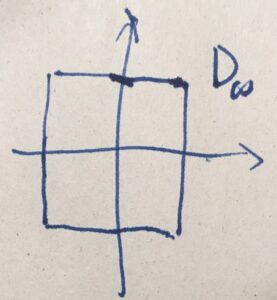
という形になります。
最大値ノルムにおける\(\infty\)は、数ではなく単なる記号です。ただしこの記号を用いるのは、
\[ \begin{aligned}\lim_{p \to \infty} \|x\|_p= \|x\|_\infty \end{aligned} \]
が成り立つからです。幾何学的には、\(D_p\)で\(p\)を大きくしていくと膨らんでいき、\(D_\infty\)に近づいていきそうな感じがしました。詳しくは、後に証明します。
同値なノルム
これまでにいくつかの\(p\)ノルムを紹介してきましたが、これらは極限や収束に関しては「同じ」性質を持っています。
1次元的な数に対して収束を考えたように、ベクトルに対してもノルムを使って収束を定義できます。ベクトルの列\((x[k])_k\)が\(a\)に収束するとは、
\[ \begin{aligned}\lim_{k \to \infty} \|x[k]-a\|_2=0\end{aligned} \]
としましょう。
例えば、\(\lim_{k \to \infty} \|(2^{\frac{1}{k}},\frac{1}{k^2})-(1,0)\|_2=0\)です。
2ノルムによる収束は、\(x[k]\)の各成分が\(a\)の各成分に収束すること(絶対値ノルムによる収束)や、成分の差の絶対値の最大値が0に収束すること(最大値ノルムによる収束)と同値になります。その理屈を説明するのが、ノルム同値という考え方です。
\(p\)ノルムの大小関係については、
\[ \begin{aligned}\frac{1}{N}\|x\| _1 \leq \|x\|_\infty \leq \|x\|_2 \leq \|x\|_1\end{aligned} \]
が成り立ちます。
一般に、2つのノルム\(\|\cdot\|_a,\|\cdot\|_b\)が同値である(equivalent)とは、定数\(C_1,C_2\)で次を満たすものが存在することです。すべての\(x\)に対し、
\[ \begin{aligned}C_1 \|x\|_a \leq \|x\|_b \leq C_2 \|x\|_a\end{aligned} \]
が成り立つ。
つまり、絶対値ノルム、ユークリッドノルム、最大値ノルムは同値です。確かめてみましょう。
まず、最大値の性質より
\[ \begin{aligned} \frac{1}{N}\|x\| _1 &=\frac{1}{N}\sum_{i=1} ^N |x_i| \\& \leq \frac{1}{N}\sum_{i=1} ^N \max_{j=1,\dots,N}|x_j| \\ &=\frac{1}{N}N \|x\|_\infty \\ &= \|x\|_\infty\end{aligned} \]
が成り立ちます。
\[ \begin{aligned} \|x\|_\infty &=( \max_{i=1,\dots,N}|x_i|^2) ^\frac{1}{2} \\ & \leq (\sum _{i=1}^N |x_i|^2 )^\frac{1}{2} \\ &= \|x\|_2 \end{aligned} \]
ここで和を取るところの不等式が成り立つのは、\(i\)すべての和を取れば、最大値となる成分をひとつは含んでいるからです。
絶対値の三角不等式\(|x+y|\leq |x|+|y|\)を使えば、
\[ \begin{aligned} \|x\|_2 &= (\sum_{i=1}^N |x_i|^2)^\frac{1}{2} \\& \leq(\sum_{i=1}^N |x_i|^2 + \sum_{i\neq j}^N |x_i||x_j|)^\frac{1}{2} \\&= ((\sum_{i=1}^N |x_i|)^2 )^\frac{1}{2}\\&= \|x\|_1\end{aligned} \]
と示せました。
同値なノルムについては、収束する点列の極限も等しくなります。例えば、
\[ \begin{aligned}\lim_{k \to \infty} \|x[k]-a\|_2=0\end{aligned} \]
ならば、ノルムの同値性から
\[ \begin{aligned}C_1 \|x[k]-a\|_2 \leq \|x[k]-a\|_1 \leq C_2\|x[k]-a\|_2\end{aligned} \]
が成り立ちます。\(C_1,C_2\)は\(k\)に依存していないことに注意して、\(k\to \infty\)の極限を取れば、はさみうちの原理から
\[ \begin{aligned}\lim _{k\to \infty} \|x[k]-a\|_1 =0\end{aligned} \]
です。1ノルムでなく、他のノルムでも同様。
最大値ノルムでは、\(\infty\)という記号を使いました。これは数ではないですが、なぜこの記号を使うかと言えば、
\[ \begin{aligned}\lim _{p \to \infty}\|x\|_p = \|x\|_\infty\end{aligned} \]
が成り立つからです。さきほどの不等式評価と同様にして、
\[ \begin{aligned} \|x\|_p & \leq(\sum_{i=1}^N \max_{j} |x_j|)^{\frac{1}{p}} \\&= N^{\frac{1}{p}} \|x\|_\infty \end{aligned} \]
\[ \begin{aligned} \|x\|_\infty &= (\max_{i} |x_i|^p)^\frac{1}{p}\\& \leq \|x\|_p \end{aligned} \]
なので、\(p\to \infty\)とすれば、\(N^\frac{1}{p}\to N^0=1\)で、はさみうちの原理から結論が言えます。
今回は、\(p\)として\(p \geq 1\)という条件をつけました。\(p<1\)のときを考えることが少ないのは、そのときはノルムの定義を満たさないからです。
例えば、\(p=\frac{1}{2}\)のとき、\((1,0),(0,4)\)を考えると、
\[ \begin{aligned}\|(1,4)\|_{\frac{1}{2}}=(1+2)^2=9 \end{aligned} \]
\[ \begin{aligned}\|(1,0)\|_{\frac{1}{2}}=(1)^2 =1\end{aligned} \]
\[ \begin{aligned}\|(0,4)\|_{\frac{1}{2}}=(2)^2=4 \end{aligned} \]
となり、三角不等式\(\|x+y\| \leq \|x\|+\|y\|\)を満たしません。
\[ \begin{aligned}\|(1,4)\|_\frac{1}{2}> \|(1,0)\|_\frac{1}{2}+\|(0,4)\|_\frac{1}{2} \end{aligned} \]
\(p<1,p \geq 1\)でノルムであるかどうかは変わります。それは\(f(x)= x^p\)のグラフが、\(p<1\)のときに上に凸で、\(p \geq 1\)のときに下に凸であることに対応したものです。
数列、関数のpノルム
今回はユークリッド空間の\(p\)ノルムを紹介してきました。それは、数列や関数の\(p\)ノルム
\[ \begin{aligned}\|x\|_{\ell ^p} =(\sum _{i=1} ^\infty |x_i|^p)^\frac{1}{p}\end{aligned} \]
\[ \begin{aligned}\|x\|_{\ell ^\infty} =\sup_{i \in \mathbb{N}}|x_i|\end{aligned} \]
\[ \begin{aligned}\|f\|_{L^p}= (\int_U |f(x)|^p)^\frac{1}{p}\end{aligned} \]
\[ \begin{aligned}\|f\|_{L^\infty} = \sup _{x\in U} |f(x)|\end{aligned} \]
の特殊なケースと言えます。
\(\sup\)は上限と呼ばれるもので、無限個の要素に対しては最大値が存在しないかも知れないので、置き換えています。上限を使ったノルムは、上限ノルム、supノルムと呼ばれるものです。
特に、関数の上限ノルム(一様ノルム)と積分ノルム(pノルム)は同値ではないことは有名です。関数空間では、考えるノルムによって、収束の意味が変わりうるのです。こうした問題は、詳しくは関数解析学で扱うことになるでしょう。
有限次元のノルム空間では、すべてのノルムが同値となることが知られています。今回紹介した\(p\)ノルムに限らず、どんなノルムを使っても収束に関する概念は等しいのです。使いやすいノルムを使って議論すれば良いということになります。
以上、pノルム、絶対値ノルム、最大値ノルムとはどういうものか、同値なノルムという考え方を紹介してきました。
ノルムといえばユークリッドノルムと思っている人もいるかもしれませんが、一般的なノルムの枠組みでは、さまざまな「測り方」を考えることができます。
数列や関数ではさまざまなノルムを考えることになりますが、その前段階として、数ベクトルのpノルムを知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870