どうも、木村(@kimu3_slime)です。
\(9-2 \times 4 \)の答えはいくつでしょうか? 掛け算の部分を先に計算するので、\(9-8=1\)ですね。
小学校や中学校では、足し算・引き算よりも、掛け算・割り算を先に計算するというルールを学びます。
こんなルールがあるのはなぜなのでしょうか。その理由を紹介します。
習慣であり、必然的な理由はない
掛け算を足し算より優先するように式を解釈ルールは、英語圏ではPEMDASと呼ばれ、日本でも同様のルールが採用されています。
さきほどは理由を紹介すると言いましたが、数学的に「そうしなければならない」必然的な理由はありません。
ただし、それはルールが無意味ということではありません。式の読み方は、「掛け算優先です」といったように、何かしら決めておかないと、答えの食い違いが生じてしまうのです。
「掛け算割り算より足し算引き算を優先する」というルールを考えることもできます。ただし、それは現代に生きている私たちの標準的な表記法ではないということです。
例えば、加減優先ルールのもとで\(9-2 \times 4 \)という式を考えれば、その答えは\(7\times 4 =28\)となります。
ただし、「式の意味を読み取るルール」はひとつである必要があります。\(9-2 \times 4 \)の答えを、ある人は\(1\)、別の人は\(28\)と考えていたら、同じ式なのに別の答えが出ることになって、困りますよね。式の意味、読み取り方は統一しておく必要があるわけです。
算数や数学は、言葉の一種です。文字や言葉というものは、それを読む人の共通認識があってこそ意思の疎通ができます。言語学者のソシュールは、「文字とその意味の間の恣意的な関係性」を論じました。
今の日本では、アラビア数字で算数・数学をするのが普通になっています。しかし、漢数字であっても変わらずに数学をすることはできるわけです。例えば和を表すのに\(+\)という記号を使う必然的な理由はなく、\(一和二=三\)と書いても数学はできます。でも、現在では普通は\(1+2=3\)と書いたほうが読み慣れている人が多いですよね。慣習の問題です。
数学では、優れた表記法が慣習として残っています。例えば、微分の表記法については、ライプニッツの記法\(\frac{dy}{dx}\)、ラグランジュの記法\(f^{\prime}(x)\)、ニュートンの記法\(\dot {x}(t)\)といった、複数の表記法が今も使われています。
しかし、互いに矛盾を導く表記法を同時に採用することはできません。\(9-2 \times 4 \)という式に唯ひとつの答えを割り当てるには、「掛け算優先」か「足し算優先」のどちらかのルールを採用する必要があり、現在では前者が採用されている、というわけですね。
似ている問題として、6÷2(1+2) という式は、「式の読み方」をはっきりさせないとバラバラの答えになってしまうことが知られています。
参考:6÷2(1+2) の答えは9?1? 出題者はカッコを使うべき
掛け算優先が定着した理由
いずれにせよ、掛け算優先のルールが、私たちの通常の式を読み解く方法となっています。
なぜそうなっているのでしょうか。さきほどまでに述べた通り必然的な理由はないですが、僕なりにそれらしい理由を推測してみましょう。
それは、掛け算を「足し算をまとめて書いたもの」と捉えたい状況がよくあって、その状況を式に表すのに簡単になるのが、掛け算優先ルールだから説です。
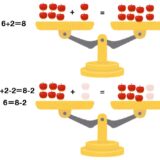
例えば、9個のアメを4人で2個ずつ分け合うことを考えましょう。掛け算を使わずにこの状況を表すと、\(9-2-2-2-2=1\)です。これは面倒くさいので、\(2\times 4 =2+2+2+2\)という掛け算記号を導入すると、\(9- 2\times 4 =1\)と表せます。
もし、足し算引き算優先のルールで同一の式を書こうとすると、\(9-(2\times 4) =1\)とカッコを必要とすることになります。「\(2\times 4\)という式が登場したら、ハナからそこは\(2\)を\(4\)回足してまとめた結果(\(8\))ですよ」と決めておくことで、カッコを使わない簡単な式で表すことができています。
中学校の数学では、数字の代わりに文字を使った式も扱うようになります。
そこでは、和\(3 +x\)はそのまま\(3+x\)と書きますが、積\(3 \times x\)のことを、\(3\cdot x\)、あるいはもっと単純に\(3x\)と書くのが「普通」の表記法です。掛け算や割り算、倍率や比率を考えるときには、そこがまとめて計算されるという前提を置いたほうが、式が単純になります。
中学では1次関数というものを学ぶかと思いますが、\(9\)個のアメを1人2個食べていく状況を考えると、\(x\)人食べたときのアメの個数\(y\)は、\(y=-2x +9\)といった関数で表せます。1次関数や2次関数、一般に関数で表せる現象は幅広く、数学や物理、広く科学でよく使うものです。
標準的な記法では、和の記号を省略せず、積の記号を省略して、
\[ \begin{aligned}y=ax ^2 +bx+c\end{aligned} \]
といったように書きます。同じ内容の式を、和を優先するスタイル、すなわち和の記号を省略して、積の記号を省略せずに書けば、
\[ \begin{aligned}y= (a\times x\times x)(b\times x ) c\end{aligned} \]
となります。まあ読めなくはないですが、カッコの数が増えているので、前者の方がシンプルですね。
(それに、関数を考えるときは、\(x\)の何乗が登場しているのかが重要で、それが簡単に読み取れる式の方が良いです。)
また、中学校の数学では、\(1,2,3\)のようなプラスの数(自然数)だけでなく、マイナスの数を含んだ整数を考えます。それは自然数の間に成り立つ法則、例えば分配法則
\[ \begin{aligned}(a-b )\times c=a\times c -b\times c\end{aligned} \]
を、\(a-b\)が\(0\)以下でも成り立つようにして、拡張された数です。
この法則を、あえて足し算優先の方法で書くと
\[ \begin{aligned}a-b \times c=(a\times c) -(b\times c)\end{aligned} \]
と2回カッコが登場することになります。掛け算優先で書いた、前者の方がシンプルですね。
以上、足し算、引き算より掛け算、割り算を優先するのはなぜかについて書いてきました。
掛け算優先でなければならない必然的な理由はなく、習慣の問題です。しかし、式の読み方を統一しないと答えがブレてしまうので、掛け算優先で読み書きしましょう、と学んでいます。数学で考えたい典型的な問題では、掛け算優先の読み方が、足し算優先の読み方に比べて、必要なカッコの数が減ってシンプルになります。
この話が、計算の順序に疑問を感じた人の答えになっていれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
6÷2(1+2) の答えは9?1? 出題者はカッコを使うべき