極値の求め方と判定条件：具体例と注意点

どうも、木村（@kimu3_slime）です。

高校数学、微分の分野では、関数が極値を持つかどうかという問題をよく考えます。

今回は、極値を持つ条件の使い方とその注意点を、具体例を交えて紹介していきましょう。

極値とはなにか
極値を持つ・持たない条件
- 極値の見つけ方
- 極値の判定条件
こちらもおすすめ

極値とはなにか

まずは言葉の確認から始めます。極値とは、極大値や極小値の総称です。

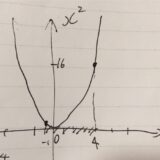
例えば、\(f(x) =x^2\)という関数では、\(x=0\)で極小値\(0\)を取ります。点\(a \)で関数が極小値を取るとは、\(a\)に近いすべての\(x\)について、\(f(a) \leq f(x)\)が成り立つことです。このときの\(a\)は極小点と呼ばれます。極大値も同様に定義されます。

3次関数\(f(x)= x(x-1)(x+1)=x^3-x\)を考えてみましょう。極値を感覚的に探すには、グラフを書いてその増減に注目すれば良いです。といっても、簡単な関数以外ではグラフの形を書くのも難しい。そこで関数の微分・導関数に注目し、増減表を書くと良いでしょう。

導関数は\(f^{\prime}(x)=3x^2 -1\)なので、\(x= \pm \frac{1}{\sqrt{3}}\)で傾きが0となります。その前後での符号を調べれば、プラスならば右上がり、マイナスならば右下がりと\(f\)の増減の傾向がつかめますね。

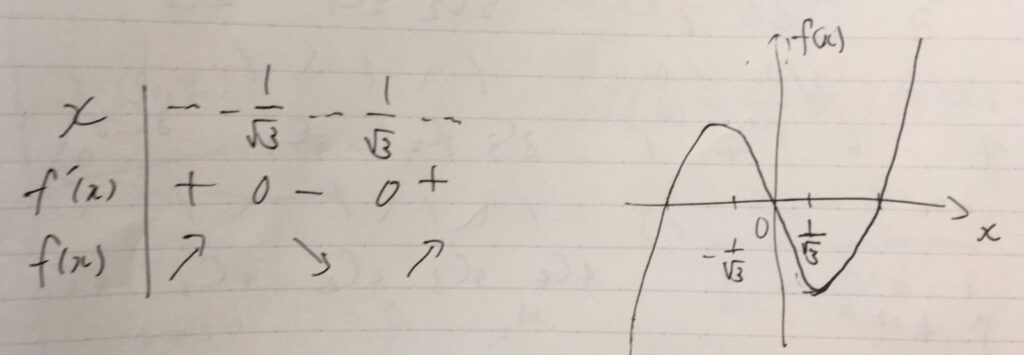
今回は、\(x= -\frac{1}{\sqrt{3}}\)が極大点、\(x= \frac{1}{\sqrt{3}}\)が極小点です。なぜそう言えるかと言えば、その点の前後で導関数\(f\)の符号が変化しているからです。極値の判定をするときはそこに注目するのが大事なのですが、「\(f^{\prime}(a) =0\)となれば良い」という部分だけが注目されやすい傾向にあります。

極大値・極小値と、最大値・最小値は区別できるようになっておきましょう。最大値や最小値は定義域全体が比較対象に入っていますが、極大値や極小値ではその点の近くだけで局所的に大きかったり小さかったりすれば良いというもの。

\(f(x)= x(x-1)(x+1)=x^3-x\)の例では、極大値や極小値はありますが、最大値や最小値は存在しません。なぜなら、\(x\)をプラスに大きくすると\(f\)はいくらでもプラスに大きな値を取りますし、\(x\)をマイナス方向に大きくすると\(f\)はいくらでもマイナスに大きな値を取るからです。全体としては最大最小に限りはないけれども、一部分だけ見ると凸や凹の形になった部分がある、という話。

極値を持つ・持たない条件

では、一般的な条件の話をしましょう。よく知られているのは、次の性質です。

極値の見つけ方

（微分可能な）関数\(f\)が\(x=a\)で極値を取るならば、\(f^{\prime} (a) =0\)

対偶を取れば、\(f^{\prime}(a) \neq 0\)となる点は、極値点とならない。

この条件の注意すべき点は、逆は成り立たないということです。つまり、\(f^{\prime}(a) =0\)となる点を見つけたからといって、必ず\(a\)が極値点であるとは言えないのです。論理の言葉で言えば、\(f^{\prime}(a)=0\)は\(a\)で極値を取るための必要条件ではあるが十分条件ではない。このことに気づくのはめちゃくちゃ大事です。

例として、\(f(x)=x^3\)という3次関数を考えましょう。導関数は\(f^{\prime}(x) =x^2\)です。\(f^{\prime} (x)=0\)を解くと、\(x=0\)が極値点の候補として見つかります。しかし、\(x=0\)は極値点ではありません。

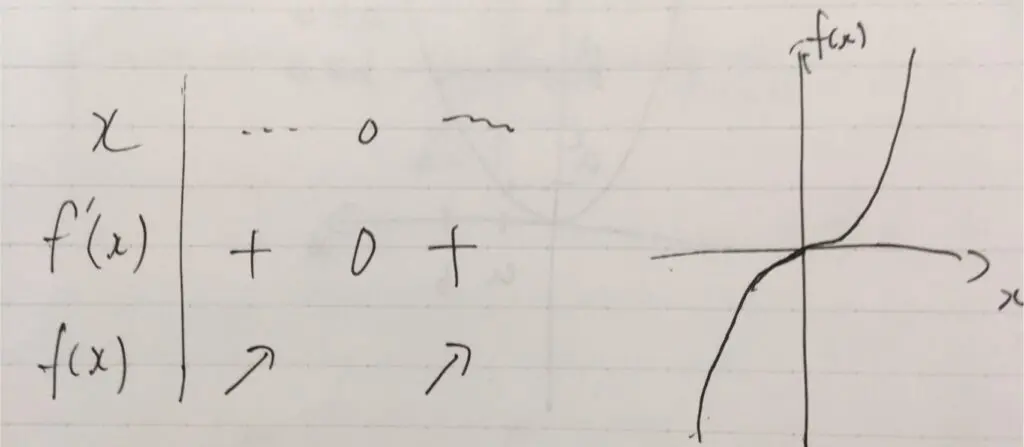
\(x=0\)が極値点ではないとは、どういうことでしょうか。例えば、\(x= -\frac{1}{10},\frac{1}{10}\)という点を考えると、\(-\frac{1}{10^3}<f(0)=0 < \frac{1}{10^3}\)という関係が成り立っています。\(f(0)\)よりも大きな値を取る点と小さな値を取る点が、\(x=0\)の近くにあるのです。

もっと一般には、\(n\)を自然数として、\(x= -\frac{1}{n},\frac{1}{n}\)を考えると、\(-\frac{1}{n^3} < f(0)< \frac{1}{n^3}\)が成り立っています。大きな\(n\)を考えれば、\(0\)にどんなに近くにも\(f(0)\)より大きくなる点と小さくなる点の両方が存在する。これが極値点ではない、ということの意味です。

細かいことを言いましたが、\(f^{\prime}(x)=0\)を解くということは、極値点を拾い上げるための大きな網に過ぎません。それで必ず極値点が求まるとは限らないのです（\(f(x)=x^3\)の例のように）。

極値の判定条件

極値の候補を見つけたら、その点の前後で凹↘↗ないし凸↗↘といったような変化をしているかを意識すると、極値かどうか判定できます。

\(f\)を2回微分できる関数とする。

「\(f^{\prime}(a )=0\)」かつ「\(x=a\)の前後で\(f^{\prime}(x)\)の符号が変化する」ならば、\(f\)が\(x=a\)で極値を取る。

さらに、次のように判定できる。

\(f^{\prime \prime}(a) >0\)ならば、\(f\)は\(x=a\)で極小値を取る
\(f^{\prime \prime}(a) <0\)ならば、\(f\)は\(x=a\)で極大値を取る

\(f^{\prime \prime}(a) \)の符号を見ると、極値点かどうか判定しやすいときがあります。「極値を求めよ」という問題なら、2階導関数が計算して、その符号で機械的に極値を求められるでしょう。

ただしこの方法には欠点があり、\(f^{\prime \prime}(a)=0\)のときはなんとも言えないことです。例えば\(f(x)=x^3\)においては、\(f^{\prime \prime}(x)=6x\)、\(f^{\prime \prime}(0)=0\)となりますが、\(x=0\)は極値点ではないのでした。

代わりに、「\(f^{\prime}(x)\)の\(x=a\)前後で符号が変化する」という条件なら一般的に使えます。ただし計算問題に使うには少し面倒かもしれません。

例として、「\(f(x) =x^3 +ax^2+2x +1\)が極値を持つような\(a\)の範囲を求めよ」という問題を考えてみましょう。

ポイントは、極値となる候補を見つけ、その点の前後で導関数\(f^{\prime}\)の符号が変化するならば、それが確かに極値となる、ということです。

導関数は、\(f^{\prime}(x)= 3x^2 +2ax +2\)です。これは\(a\)によって形状が変わります。\(f^{\prime}(x)=0\)一般的に解けば、解の公式により

\[ \begin{aligned}x= \frac{-2a \pm \sqrt{4a^2 -24}}{6}\end{aligned} \]

となりますが、ここまで表示する必要はありません。問題は、\(f^{\prime}(x)=0\)が、\(a\)の値に応じていくつ解を持つか、そのときに符号の変化がどうなるか、ということです。つまり、ルートの中身、判別式\(D = 4a^2 -24\)の符号が重要です。場合分けして考えましょう。

\(D>0\)のとき、\(f^{\prime}(x)=0\)は2つの実数解を持ち、\(f^{\prime}(x)\)はその前後で符号を変化させます。つまり、その2つの解は極値点となります。
\(D=0\)のとき、\(f^{\prime}(x)=0\)は重解を持ち、\(f^{\prime}(x)\)はその前後で符号がプラスのままです。したがって、その点は極値点ではありません。（\(f(x)=x^3\)で得た考察と同様）
\(D<0\)のとき、\(f^{\prime}(x)=0\)は実数解を持たず、常に\(f^{\prime}(x)>0\)となります。したがって、極値点を持ちません。

以上をまとめると、\(D>0\)のときのみ、極値を持ちます。\(4a^2-24 >0\)を解けば、\(a<-\sqrt{6}\)または\(\sqrt{6}< a\)のとき、\(f\)は極値を持つことがわかりました。

これによって、「\(f(x) =x^3 +ax^2+2x +1\)が極値を持たないような\(a\)の範囲を求めよ」という問題も解けています。それは\(D \leq 0\)のときで、\(-\sqrt{6} \leq a \leq \sqrt{6}\)という範囲です。