どうも、木村(@kimu3_slime)です。
高校数学の数と式の分野では、不等式の扱いについて学びますが、慣れていないと間違った議論をしやすいです。
今回は、\(-1 \leq x \leq 4\)のようなマイナスの範囲を含む不等式を二乗したいときの注意点を紹介します。
不等式とマイナスの影響
よくある間違い
実数\(x\)が\(-1 \leq x \leq 4\)の範囲を取るとき、\(x^2\)の取りうる値の範囲を求めよ、という問題について考えてみましょう。
よくある間違いが、次のようなものです。
\(-1 \leq x \leq 4\)の各辺を二乗すれば、\(1 \leq x^2 \leq 16\)。
これは誤りです。例えば、\(x=0\)は\(-1 \leq x \leq 4\)を満たしますが、\(1 \leq 0 \leq 16\)は誤りです。
グラフを書いてみると、この誤りがどうして起こっているのか見えやすくなります。
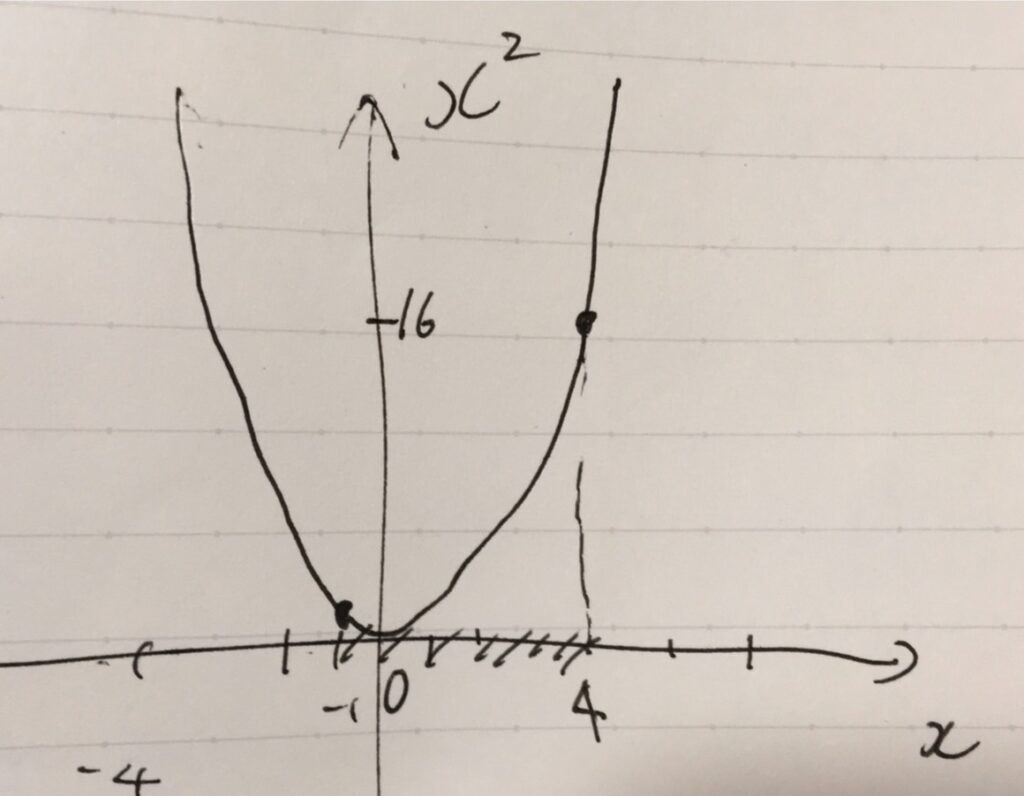
\(f(x)=x^2\)のグラフは、\(-1 \leq x \leq 4\)の範囲において、\(x=0\)で最小値\(0\)、\(x=4\)で最大値\(16\)を取っています。つまり、答えとしては\(0 \leq x^2 \leq 16\)が正解です。
この視覚的イメージがあれば、\(1 \leq x^2 \leq 16\)という結論は、\(x^2\)が1より小さくなる部分を無視してしまっていることに気づくはずです。
等式と不等式の違い
さて、どうして不等式の各辺をそのまま2乗してはいけなかったのでしょうか。端的に言えば、不等式には向きがあり、マイナスをかけると向きが変わってしまうからです。
このことは、等式と比較してみるとわかりやすくなります。例えば\(x=3\)という等式を考えます。\(x=3\)が正しいとき、両辺を2乗した\(x^2 = 9\)という式は正しいです。(この逆:\(x^2=9\)ならば\(x=3\)は正しくないことに注意しましょう。\(x=3\)または\(x=-3\)です。)
\(a,b\)がどんな実数であっても、\(a=b\)ならば\(a^2 =b^2\)が成り立ちます(等式の性質)。
不等式では、2乗するときに注意が必要です。
例えば、\(x\geq 2\)ならば、\(x^2 \geq 4\)という推論は正しいです。
しかし、\(x\leq -2\)ならば、\(x^2 \leq 4\)という推論は正しくありません。例えば、\(x=-3\)のとき、\(x^2=9\)となってしまいます。正しくは、\(x^2 \geq 4\)と向きを逆にした不等式です。
この2つの例の違いは、両辺ともプラス(非負)であるかどうか、ということです。\(a \geq 0 \)かつ\(b \geq 0\)であり、\(a\leq b\)ならば、\( a^2 \leq b^2\)が成り立ちます。両辺がマイナスでないならば、二乗しても同じ向きの不等式が成り立つのです。
\(x\leq -2\)のようなケースは、両辺ともマイナスです。\(a < 0 \)かつ\(b< 0\)であり、\(a\leq b\)ならば、\( a^2 \geq b^2\)が成り立ちます。両辺ともマイナスのときは、二乗すると逆向きの不等式となるわけです。
これらの結論は、「2乗したら不等号が逆になる」と形だけ覚えるのでなく、\(x\)に具体的な値を当てはめて考えたり、グラフを描いて位置関係を調べるのが良いと思います。

第2のケースは、\(x\leq 3\)といった不等式の両辺にマイナスをかけたケースに似ています。両辺にマイナス1をかけて\(-x \leq -3\)であると考えるのは間違いで、\(-x \leq -3\)と向きが逆になりますよね。
\(a\leq b\)という不等式に、何か数\(c\)をかけるときは、\(c\)がプラスかマイナスかが重要です。\(c \geq 0\)のときは、\(ca \leq cb\)と向きが保たれます。一方で、\(c<0\)のときは、\(ca \geq cb\)と逆向きになります。不等式における掛け算や2乗を考えるときは、等式と違って、「マイナスによって向きが変わらないか?」と注意する必要があるわけです。
「実数\(x\)が\(-1 \leq x \leq 4\)の範囲を取るとき、\(x^2\)の取りうる値の範囲を求めよ」という問題を、場合分けして再び考えましょう。
- \(-1 \leq x \leq 4\)のとき、\(x\)は\(-1 \leq x <0\)または\(0 \leq x \leq 4\)を満たす。
- \(-1 \leq x <0\)のとき、各辺はマイナスです。このとき、取りうる値は\(0 < x^2 \leq 1\)となります。
- \(0 \leq x \leq 4\)のとき、各辺はプラスです。このとき、取りうる値は\(0 \leq x^2 \leq 16\)となります。
- 場合分けの結果を合わせれば、取りうる値は\(0 \leq x^2 \leq 16\)です。
各辺がマイナスとなる場合に気をつけて場合分けして考えると、不等式の問題は正しい結論を得ることができるでしょう。
不等式と2乗に関連する問題
不等式と2乗に関する問題を、いくつか紹介しましょう。
ルートを含む不等式
実数\(x\)が不等式\(\sqrt {x^2+1} \geq -\sqrt{10}\)を満たすとき、\(x\)の取りうる値の範囲を求めよ。
間違った回答をあえて書きます。両辺を2乗すれば、\(x^2 +1 \geq 10\)が得られる。よって、\(x^2 \geq 9\)となる。求める範囲は\( x \leq -3 \)または\(x \geq 3\)。
上の回答では、\(x\)の取りうる値の一部しか捉えられていません。例えば、\(x=0\)は\(\sqrt{0^2 +1} \geq -\sqrt{10}\)を満たしていますが、\( x \leq -3 \)または\(x \geq 3\)の範囲に含まれていません。
正しく考えるには、まず左辺が常にプラスであり、右辺がマイナスであることに注目しましょう。特に、\(\sqrt{x^2+1} \geq 0\)なので、\(x^2 +1 \geq 0\)が成り立ちます。\(x\)がなんであっても、\(x ^2 \geq 0 > -1\)は成り立っていますね。したがって、\(x\)の取りうる範囲はすべての実数であるとわかりました。
\(\geq -\sqrt{10}\)という右辺の条件は、左辺に影響しない見せかけの条件だったわけです。左辺は常にプラスだよね、右辺は常にマイナスだよね、といった確認を、数直線上に点を描くなどしてイメージすると、間違いが減るでしょう。
4次関数の取りうる値について
\(f(x)= x^4 -2x^2 +4\)が、\(-1 \leq x \leq 4\)のとき取りうる値を求めよ。
といった問題は、\(t= x^2\)とおくことで、\(f(t)= t^2-2t+4=(t-1)^2 +3\)の取りうる値の問題に置き換えられます。ここで\(t=x^2\)の変化しうる値を求める必要があり、さきほどまでの考え方が必要です。
\(-1 \leq x\leq 4\)のとき、単に両辺を2乗するのではなく、\(0 \leq t=x^2 \leq 16\)となります。この範囲では、\(f(t)\)は\(t=1\)で最小値、\(t=16\)で最大値を取りますね。\( 3 \leq f(t) \leq 15^2+3\)となります。
二乗の外し方
\(x\)が不等式\(x^2 \geq 5\)を満たすとき、\(x\)の取りうる範囲を求めよ。
これはもとの不等式を2乗したいという問題の逆、2乗を含む不等式から2乗を外したい、という問題です。
これもグラフを書くとイメージしやすいですね。\(x^2=5\)が成り立つのは、\(x= \sqrt{5}\)、または\(x=- \sqrt{5}\)のときで、左辺\(x^2\)の方が大きくなるのは「外側」の部分です。つまり、\(x \leq -\sqrt{5}\)、または\(x \geq \sqrt{5}\)が\(x\)の取りうる範囲となります。
問題が「\(x^2 \leq 5\)を満たす」という問題なら、\( -\sqrt{5} \leq x \leq 5\)となりますね。
もう少し形を変えてみるとどうでしょうか?
「\(x ^2 \leq 0\)を満たす」という問題ならば、\(x=0\)のみです。
「\(x^2 \leq -1\)を満たす」ならば、これを満たす実数\(x\)は存在しません。
こうした問題でも、両辺がプラスとなるか、マイナスを含むかによって状況が変わってくるわけですね。
以上、不等式を2乗するときの注意点、マイナスを含んでいないかどうかについて紹介してきました。
等式の場合と違い、不等式を考えるときは「両辺を2乗する」「両辺を定数倍する」といった操作をするときに、マイナスが含まれているかどうかという条件が重要になってきます。それによって、不等式の向きが変わったり、単純な変形ができないことがあるからですね。
いずれにしても、不等式の問題では、(書けるなら)図を書いて考えるのが大事だと思います。数の大小関係を視覚的に理解すれば、間違った論理展開を減らせるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。