どうも、木村(@kimu3_slime)です。
高校数学の図形と方程式の分野では、2直線の交点を通る直線を
\[ \begin{aligned}ax+by+c +k(a^{\prime}x +b^{\prime }y +c^{\prime})=0\end{aligned} \]
と\(k\)を使って表す、という考え方をすることがあります。これはなぜなのか、簡単な例からわかりやすく紹介していきましょう。
1点を通る直線の方程式
まず問題を分割して、ある1点を通る直線の方程式はどのように表されるか、について考えましょう。
例えば、原点\((0,0)\)を通る直線の方程式はどう表したら良いでしょうか。\(y=x\)、\(y=2x\)、\(y=\frac{1}{2} x\)、いろいろな直線がありますね。
直線は例えば、一次関数\(y=ax+b\)で表されますが、\(a\)を\(k\)に置き換えて、原点を通ることから\(b=0\)とすれば
\[ \begin{aligned}y=kx\end{aligned} \]
と表されます。何らかの直線が与えられたときに、それに応じて傾き\(k\)を決めれば良いわけです。
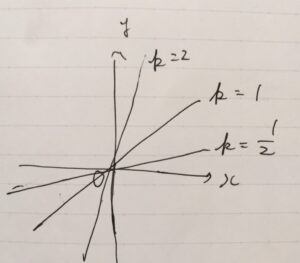
ただし、これで原点を通る「全ての」直線が表されているわけではないことに注意しましょう。\(y\)軸に平行な直線、\(x=0\)は\(y=kx\)の形には表されませんが、原点を通る直線の方程式ではあります。
2直線の交点を通る直線の方程式
では、2つの直線の交点を通る直線の方程式について考えましょう。
簡単な例として、\(y=x\)と\(y=3x -6\)の交点を通る直線の方程式を表したいとします。
交点を具体的に求めるなら、\(y=x\)と\(y=3x-6\)の両方を満たす\((x,y)\)を探せば良いです。これを解けば、\(x=3,y=3\)が得られます。
\((3,3)\)を通り、傾きが1の直線は、\(y=(x-3)+3\)です。この傾きを\(k\)と一般的に表せば、\(y=k(x-3)+3\)が、2直線の交点を通る直線の方程式となりました。
\(k\)の値が何であろうが、\(x=3,y=3\)はこの方程式を成り立たせていることを確かめてみてください。
この方程式\(y=k(x-3)+3\)はぱっと見だと、
\[ \begin{aligned}ax+by+c +k(a^{\prime}x +b^{\prime }y +c^{\prime})=0\end{aligned} \]
という形をしていないので、この形がどうやったら得られるか考えてみます。
少し見方を変えて、2の直線\(y=x\)と\(y=3x-6\)の両方を満たす点\((x,y)\)を考えましょう。それは交点そのものですが、ここではそれを具体的に表さず、\((x,y)\)のまま話を進めます。言い換えれば、
\[ \begin{aligned}-x+y=0\end{aligned} \]
\[ \begin{aligned}-3x+y+6=0\end{aligned} \]
の両方を満たします。ここで一方の式を、適当に\(k\)倍しても、右辺は\(0\)なので、
\[ \begin{aligned}k(-3x+y+6)=0\end{aligned} \]
が成り立ちます。そして2つの方程式を足し合わせると、
\[ \begin{aligned}(-x+y)+k(-3x+y+6)=0\end{aligned} \]
が得られました。
この方程式は、そもそもが\((x,y)\)が\(y=x\)と\(y=3x-6\)の両方を満たすという条件で進めたので、交点を通っています。実際、交点\((3,3)\)を代入してみると、成り立っていることを確かめてみてください。
さらに、この方程式は直線の方程式です。なぜなら、\(x,y\)について整理すると
\[ \begin{aligned}(-3k-1)x+(k+1)y+6k=0\end{aligned} \]
です。これは\(ax+by+c=0\)という直線の方程式の形をしていますね。\(k \neq -1\)のときは、傾きが\(\frac{3k+1}{k+1}\)の直線です。\(k=-1\)のときは、\(y\)の部分が消え、\(x=3\)という直線になっています。
途中で、直線の方程式の一方を\(k\)倍しましたね。
なぜそんなことをするかといえば、交点を通るいろいろな直線の式を文字\(k\)を使って表したいからです。
\(k\)を使わずに書くと、例えば\((-x+y)+1(-3x+y+6)=0\)も2つの直線の交点を通る直線の方程式です。しかし、それは傾きが\(2\)の特殊なものでしかありません。
「2つの直線の交点と、もうひとつ別の点を通る直線の方程式を求めよ」という問題を考えたいとします。交点を通るたくさんの直線の式を文字\(k\)を使って表しておけば、その別の点が決まったときに\(k\)を具体的に求められて、便利ですね。
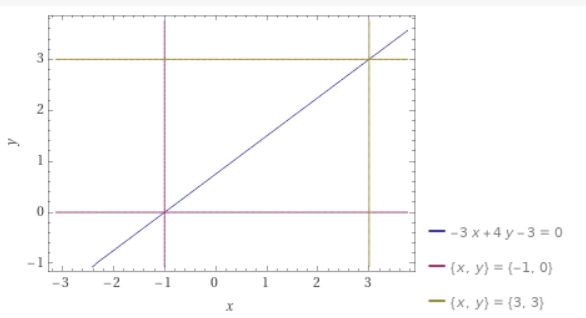
試しにやってみましょう。\(y=x\)と\(y=3x-6\)の交点を通り、\((-1,0)\)を通る直線の方程式を求めてみます。
\(k\)を実数として、
\[ \begin{aligned}(-x+y)+k(-3x+y+6)=0\end{aligned} \]
という方程式は、2直線の交点を通る直線の方程式です。そして、\((-1,0)\)を通るので、それを代入すれば、
\[ \begin{aligned}1+0+k(3+0+6)=0\end{aligned} \]
より、\(k=-\frac{1}{9}\)です。よって、
\[ \begin{aligned}-\frac{2}{3}x +\frac{8}{9}y -\frac{2}{3} =0\end{aligned} \]
整理して
\[ \begin{aligned}-3x +4y -3 =0\end{aligned} \]
が求める直線の方程式であるとわかりました。
画像引用:Wolframalpha
一般化
以上で述べたことを一般化します。
直線\(f(x,y)=ax+by+c \)と直線\(g(x,y)=a^{\prime}x +b^{\prime }y +c^{\prime}\)の交点を通る直線の方程式を一般的な形で表したいとします。定数\(k\)を使って
\[ \begin{aligned}ax+by+c +k(a^{\prime}x +b^{\prime }y +c^{\prime})=0\end{aligned} \]
\[ \begin{aligned}f(x,y)+k g(x,y)=0\end{aligned} \]
と表される直線は、2直線の交点を通っています。
なぜなら、\(x,y\)が交点であるならば、\(f(x,y)=ax+by+c =0\)と\(g(x,y)=a^{\prime}x +b^{\prime }y +c^{\prime}=0\)を同時に満たしているので。
\(k\)はどちらにつけても大丈夫です。
\[ \begin{aligned}kf(x,y)+g(x,y)=0\end{aligned} \]
も、2つの直線の交点を通る直線の方程式ですね。\(x,y\)が交点ならば、\(f=0,g=0\)が両方成り立つので。
ただし、2直線の交点を通る「すべての」直線が、\(k\)を使って\(f(x,y)+k g(x,y)=0\)と表される、とは言っていないことに注意しましょう。これを答案に述べたら間違いです。
\(k\)がかかっている方の直線\(g(x,y)=a^{\prime}x +b^{\prime }y +c^{\prime}\)は、この方程式では表せていません。なぜなら、必ず\(f +kg=0\)において\(f\)という直線が加わって、式の形が変わっているからです。一方、\(f=0\)という直線は、\(f+0g=0\)と\(k=0\)のケースとして表されています。
これは冒頭に考えた、\(y=kx\)と似た状況です。この方程式によって多くの直線を表すことができますが、\(x=0\)という直線はどうやってもこの式では表現できていないのです。
2つの数を導入すれば、すべての直線が表せます。2直線の交点を通る方程式は、\(k,\ell\)を少なくとも一方が0でない数として、\(kf+\ell g=0\)と表せるのです。ただし\(k,\ell\)と2つの数があると問題を解くのに使いにくいので、とりあえず\( f+kg=0\)の形の直線を考えれば十分実用的だろう、ということなのでしょう。
問題の回答で述べるには、「\(k\)を何らかの数とすると、\(f(x,y)+k g(x,y)=0\)は2つの直線の交点を通る直線である」というのが適切ですね。とりあえずパラメーター\(k\)を導入して表せる直線についてまず考える。すると……という議論をすれば良いわけです。
さらにこの考え方を発展させた問題として、2つの直線でなく、円を考えることができます。\(f,g\)を円を定める式として、\(k\)を何らかの数として、
\[ \begin{aligned}f(x,y)+kg(x,y)=0\end{aligned} \]
を考えると、2つの円の共通点、交点を通る図形の方程式となります。
以上、2直線の交点を通る直線をなぜkを使って表すかにっついて、具体例を交えながら紹介してきました。
\(k\)を使うことで、ある点を通る様々な直線をひとつの式で表すことができます。
もちろん\(k\)を使わずに、地道に交点を求めて、2つの点を通る直線の式を求めるのも良いと思います。
ただし、\(f(x,y)+kg(x,y)=0\)が2つの図形の共通する点を通る方程式に見えると、より発展的な問題が解きやすくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。