どうも、木村(@kimu3_slime)です。
今回は、関数列の収束、各点収束、一様収束、\(L^p\)収束について紹介します。
関数列の収束とは
各自然数\(n \in \mathbb{N}\)に対し、数\(a_n\)が定まっている時、それを順に並べたもの\(\{a_n\}_{n \in \mathbb{N}}\)を数列というのでした。
これと同様に、各\(n\in \mathbb{N}\)に対し、関数\(f_n\)が定まっている時、\(\{f_n\}_{n \in \mathbb{N}}\)を関数列といいます。
例えば、\(I=[0,1]\)を関数の定義域としましょう。\(f_n(x):= x^n\)と定めれば、これは関数列です。
この関数は、\(n\to \infty\)でどんな関数に収束するのでしょうか? \(f_1(x)=x\)は1次関数、\(f_2(x)=x^2\)は2次関数ですね。グラフを描けば次のようになります。
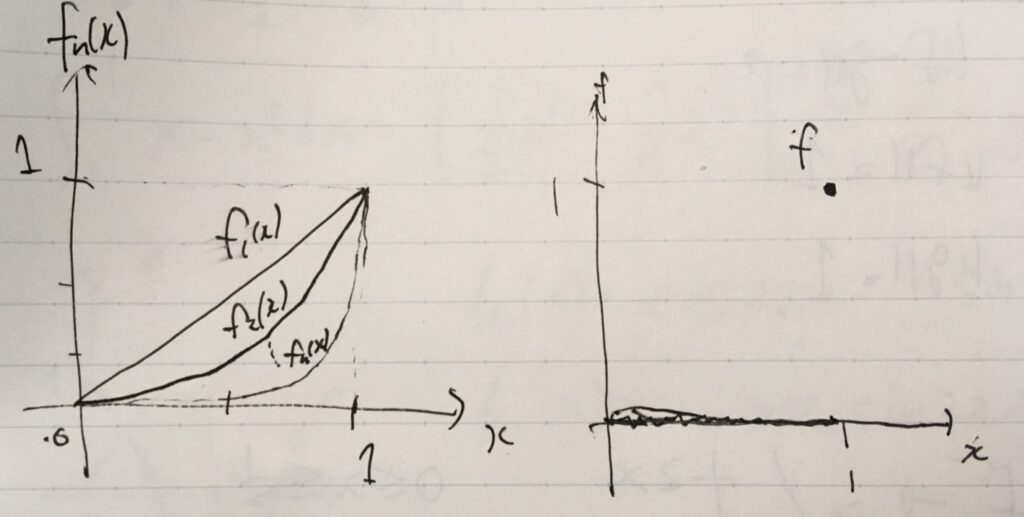
関数列\(\{f_n\}\)が\(f\)に各点収束(pointwise convergence)するとは、各点\(x\)に対して、\(\lim_{n\to \infty} |f_n(x)-f(x)|=0\)が成立することです。
さきほどから考えている関数列\(f_n(x):= x^n\)ならば、
\[ \begin{aligned}f(x)= \begin{cases}0 & (0\leq x <1 )\\1 & (x=1)\end{cases}\end{aligned} \]
に各点収束しています。\(x\)を\(0 \leq x <1\)とするとき、1より小さい数をべき乗していくとどんどん小さくなり、\(x^n \to 0 \,( n\to \infty)\)ですね。一方、\(x=1\)のときは、\(1^n =1 \to 1 \,( n \to \infty)\)です。よって、\(f_n\)は\(f\)に各点収束しています。
ここからは、関数が属している空間(関数空間)を意識してみましょう。
\(f_n(x):= x^n\)はそれぞれが連続関数であり、連続関数のなす空間\(C(I)\)の点列と言えます。にもかかわらず、極限関数\(f\)は連続ではありませんでした。
関数列の収束には、関数の距離・ノルムの選び方によっていくつかのパターンが考えられます。
\[ \begin{aligned}\|f\|_{C^0(I)}:= \sup _{x \in I} |f(x)|\end{aligned} \]
\[ \begin{aligned}\|f\|_{L^1(I)}:=\int_I |f(x)| dx\end{aligned} \]
で定まるノルムを、それぞれ上限ノルム(一様ノルム)、\(L^1\)ノルムと呼びます。これらのノルムに関する関数列の収束
\[ \begin{aligned}\lim _{n\to \infty} \|f_n -f\|_{C^0(I)}=0\end{aligned} \]
\[ \begin{aligned}\lim _{n\to \infty} \|f_n -f\|_{L^1(I)}=0\end{aligned} \]
をそれぞれ、一様収束(uniform convergence)、\(L^1\)収束(\(L^1\) convergence)といいます。
\(f_n(x):= x^n\)は\(f\)に一様収束していません。なぜなら、常に\(\| f_n-f\|_{C^0(I)} = \sup_{x\in I} |x^n|=1\)だから、\(\lim _{n\to \infty} \|f_n -f\|_{C^0(I)}=1 \neq 0\)です。\(x=0,1\)という端点では、常に\(f_n,f\)の値は一致しているので、そこでの差は0として考えなくて良いです。内部における2つの関数の差は、\(x^n\)であり、それは常に\(1\)より小さく、\(x\)が\(1\)に近づくにつれて限りなく\(1\)に近い値を取ります。\(1\)はほぼ「最大値」なのですが、内部においては実際は\(1\)の値を取りません。このような状況を捉えているのが、\(\sup|x^n|=1\)、上限という考え方ですね。(上限については、別記事で解説するかもしれません)
一方で、\(L^1\)ノルムについて考えます。\(\|f_n -f\|_{L^1(I)}=\int_0 ^1 |x^n| dx =\frac{1}{n}\)なので、\(\lim _{n\to \infty} \|f_n -f\|_{L^1(I)}=0\)であり、\(L^1\)収束していることがわかりました。
つまりこの例は、各点収束、\(L^1\)収束するけれども、一様収束はしない関数列と言えます。
別の例を考えましょう。\(J= \mathbb{R}\)を定義域とし、\(g_n(x) = \frac{1}{n} \sin x\)とします。
各点では、常に値が0である関数\(g(x)=0\)に収束していますね。
上限ノルムを考えると、三角関数の部分は常に\(1\)以下なので、\(\|g_n-g\|_{C(J) }\leq \frac{1}{n}\)であり、\(\lim _{n\to \infty} \|g_n -g\|_{C^0(J)}=0\)と一様収束していることがわかります。
一方で、\(L^1\)ノルムについて考えます。各\(n\)に対して、\(\|g_n-g\|_{L^1(J)}= \int _{\mathbb{R}} \frac{1}{n}\sin x dx =\infty\)です。例えば\([0,2\pi ]\)において、積分は常に正の値を持ち、それが実数全体に渡って足されるので、限りなく大きな値を持ち、積分可能ではありません。したがって、\(\lim _{n\to \infty} \|g_n -g\|_{L^1(I)}=0\)は成り立たず、\(L^1\)収束していません。
関数列\(g_n\)は、各点収束、一様収束しているけれども、\(L^1\)収束はしていない例と言えます。
\(I\)において\(h_n (x)= \frac{x}{n}\)とすると、各点収束、一様収束、\(L^1\)収束の極限は一致します。
たとえ各点収束している関数の列があったとしても、その収束の仕方は関数列によって多種多様になりうるわけですね。
ちなみに、ユークリッド空間\(\mathbb{R}^N\)でもいくつかの距離・ノルムの与え方を考えることができます。
そこではしかし、今回のように「あるノルムでは収束するがあるノルムでは収束しない」ということは起こりえません。一般に、「有限次元のノルム空間ではすべてのノルムが同値である」ことが知られており、実質的には収束の種類は1種類となります。
関数空間は一般に無限次元であり、あるノルムでは収束するが、別のノルムでは収束しない、ということが起こり得るわけです。だからこそ、関数列の収束を考える時は、どんなノルムで収束しているのか意識する必要があります。
収束に関する性質
\(L^1\)ノルムの一般化として、\(1 \leq p < \infty\)として、
\[ \begin{aligned}\|f\|_{L^p(I)}:=(\int_I |f(x)|^p dx)^\frac{1}{p}\end{aligned} \]
\[ \begin{aligned}\lim _{n\to \infty} \|f_n -f\|_{L^p(I)}=0\end{aligned} \]
を、\(L^p\)ノルム、\(L^p\)収束と言います。
一様収束や\(L^p\)収束については、数多くの性質が知られています。その主張の一部を列挙していきましょう。
- 一様収束するならば、その極限関数は連続である。(一番最初に考えた例では、不連続な関数に各点収束していたので、この主張から一様収束していないと言えます。逆は一般に成り立たないことに注意。)
- 有界閉区間上で一様収束しているならば、関数列の極限と微分や積分との順序交換ができる。
- コンパクト集合上の連続関数のなす空間は、一様ノルムを入れると完備である。
- 関数列は、収束する無限級数によって抑えられているならば、一様収束する(ワイエルシュトラスのMテスト)。
- 連続関数列は、ある条件を満たすならば一様収束する部分列を持つ(アスコリ・アルツェラの定理)。
- 各点収束する可積分な関数列で、\(n\)につき単調増加であるならば、\(L^1\)収束する(単調収束定理)。
- 各点収束する\(p\)乗可積分な関数列で、それが一様にある\(p\)乗可積分な関数に抑えられるならば、\(L^p\)収束する(優収束定理)。
- \(p\)乗可積分の関数のなす空間\(L^p\)は、\(L^p\)ノルムについて完備である。
- パラメータを含む積分で定義される関数は、被積分関数の微分がある可積分関数におさえられるならば、微分と積分を順序交換できる。
特に重要なのは、「項別に」微積分して良いかどうか、という問題です。
\[ \begin{aligned}\lim _{n\to \infty}\int_I f_n(x)dx = \int _I \lim _{n\to \infty} f_n(x) \end{aligned} \]
\[ \begin{aligned} \lim _{n\to \infty}\frac{df_n}{dx} (x) =\frac{d}{dx}(\lim_{n\to \infty} f_n(x))\end{aligned} \]
ここで\(f_n\)を関数項級数\(\sum _{k=1}^n f_k\)に置き換えたケースもよく考えます。
この問題に対して回答を与えてくれるのが、一様収束やルベーグ積分、関数解析の理論と言えるでしょう。
以上、関数列の収束、各点収束、一様収束、\(L^p\)収束について具体例を挙げながら紹介してきました。
微分方程式を扱うためには、関数を近似する級数や関数列を扱う必要があります。それが収束したとしても、「どんな意味(ノルム)で」収束しているのかが大事で、それによって気軽に極限の順序交換をして良いかどうかが変わってきます。
少し難しい話もあったかもしれませんが、関数列の極限には、上限や積分値など、複数の捉え方(ノルム)があることを感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-06T00:00:00.000Z)
¥2,640
日本評論社 (2000-12-01T00:00:01Z)
¥2,420
共立出版 (1980-11-01T00:00:01Z)
¥5,390