バーコード、ISBNのチェックディジットとは？計算してみよう

どうも、木村（@kimu3_slime）です。

今回は、バーコードやISBNに見られるチェックディジットとは何か、計算例を紹介します。

バーコード、チェックディジットとは何か
チェックディジットを計算してみよう
ISBNのチェックディジット
チェックディジットの原理
こちらもおすすめ

バーコード、チェックディジットとは何か

僕たちが目にする商品には、バーコードがついています。スーパーやコンビニのレジでは、それをスキャンすることで、商品名と値段が一瞬でカウントされますね（POSシステム）。

バーコードのバーは、13桁の数字を読み取りのために符号化したものです。つまり、その13桁の数字が商品を特定するためのコードとなっています。広く、GTIN（Global Trade Item Number 商品識別コード）と呼ばれる仕組みが採用されています。

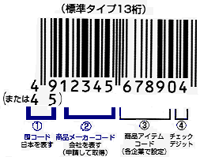
画像引用：バーコード篇(1)　バーコードの仕組み – 日本NCR株式会社

バーコードの前半9桁は、GS1事業者コードと呼ばれ、どこの国の商品か、商品のメーカーはどこかを表しています。後半の4桁は、そのメーカーにおける商品を識別する3桁のコードに、チェックディジット1桁が合わさったものです。

今回注目したいのは、チェックディジットです。日本語で言えば、検査数字。

商品を特定するためには「国・メーカー・商品種類」を表す12桁で足りるわけですが、その12桁からある法則によって決まる1桁の数字がチェックディジットです。

何のためにそれがあるかといえば、その12桁の数字の記載ミスを防ぐためですね。世界中のメーカーは商品を生み出し、それにバーコードを記載しています。もしチェックディジットがなければ、何かしらのミスで、間違えたコードを記載してしまう可能性があります。そうした間違いの可能性を減らす仕組みが、チェックディジットです。

チェックディジットを計算してみよう

では、バーコードのチェックディジットの仕組みを確認し、計算してみましょう。

バーコードの12桁の部分を\(a=(a_{1}a_{2}\cdots a_{11} a_{12})_{10}\)と、左から\(k\)番目の数を\(a_k\)と表すことにします。そのチェックディジットは、モジュラス10ウェイト3・1と呼ばれる方式で定まっています。奇数番の数そのまま足し、偶数番は3倍して足し、それを10で割った余りの数字を、10から引いた数字です。合同式を使った数式で言えば、

\[ \begin{aligned}x \equiv \sum_{k=1}^{6} (a_{2k-1} +3a_{2k})\,(\mathrm{mod} \,10)\end{aligned} \]

を満たす整数\(1\leq x \leq 10\)を求めたとき、\(a_{13}=10-x\)がチェックディジットである、という定義となります。

（何番目かに応じて倍数を変えることは、重み付きの和を考える、と呼ばれることです。重みがない単純な和より、誤りが検出しやすくなります。）

参考：倍数同士の和は同じ倍数となること、整数の合同modとは、合同式の性質を使った整数の余りの計算方法

算数レベルの問題なので、試しにやってみましょう。最近ハマっているニュータッチのカップ麺のバーコードのチェックディジットを求めてみます。

\((4903,0880,0887)_{10}\)という12桁がありました。チェックディジット\(5\)となっていますが、これはあっているのでしょうか？

奇数番の合計は\(4+0+0+8+0+8=20\)、偶数番の合計は\(9+3+8+0+8+7=35\)です。偶数番を3倍して両者を足すと\(125\)で、\(10\)で割ったあまりは\(5\)です。すなわち、

\[ \begin{aligned} \sum_{k=1}^{6} (a_{2k-1} +3a_{2k}) \equiv 125\equiv 5\,(\mathrm{mod} \,10)\end{aligned} \]

で、チェックディジットが確かに\(10-5=5\)であることがわかりました。

もうひとつやってみましょう。\((4903,0880,1175)_{10}\)から、チェックディジットを求めてみます。

奇数番の合計は\(4+0+0+8+1+7=20\)、偶数番の合計は\(9+3+8+0+1+5=26\)です。したがって、

\[ \begin{aligned} \sum_{k=1}^{6} (a_{2k-1} +3a_{2k}) \equiv 98 \equiv 8\,(\mathrm{mod} 10)\end{aligned} \]

で、チェックディジットが\(10-8=2\)であることがわかりました。これは実際のコードと一致しています。

ISBNのチェックディジット

書籍にもバーコードがついていますが、さきほどまでのGTINではなく、ISBN（International Standard Book Number 国際標準図書番号）が採用されています。本を識別する番号、という点ではGTINと同じです。

2007年頃までは10桁の数字でしたが、それ以降はGTIN同様13桁の数字で、チェックディジットの計算法も同様となっています。（ISBN-10ではチェックディジットの計算法が少し違う（モジュラス11 ウェイト10-2））

試しに計算してみましょう。2つのコードがありますが、どちらも一番最後の数字がチェックディジットです。

\((9784,8156,0145)_{10}\)について。奇数番の合計は\(9+8+8+5+0+4=34\)、偶数番の合計は\(7+4+1+6+1+5=24\)です。したがって、

\[ \begin{aligned} \sum_{k=1}^{6} (a_{2k-1} +3a_{2k}) \equiv 106 \equiv 6\,(\mathrm{mod} 10)\end{aligned} \]

で、チェックディジットが\(10-6=4\)であることがわかりました。

\((1920,0210,1500)_{10}\)について。奇数番の合計は\(1+2+0+1+1+0=5\)、偶数番の合計は\(9+0+2+0+5+0=16\)です。したがって、

\[ \begin{aligned} \sum_{k=1}^{6} (a_{2k-1} +3a_{2k}) \equiv 53 \equiv 3\,(\mathrm{mod} 10)\end{aligned} \]

で、チェックディジットが\(10-3=7\)であることがわかりました。以上の結果は、実際のコードと一致しており、このバーコードに誤りはないであろうと考えられますね。

チェックディジットの原理

チェックディジットがあると、1つの数だけ間違えたようなケースを検出することができます。

\(a_{\ell}\)が\(a_{\ell^{\prime}}\)に間違えられた（\(a_{\ell} \neq a_{\ell^{\prime}}\)）としましょう。このとき、チェックディジットを求める式\(\sum_{k=1}^{6} (a_{2k-1} +3a_{2k})\)の差は、\(k(a_{\ell}-a_{\ell^{\prime}})\)、\(k\)は\(1\)または\(3\)となります。

一般に、\(c,n\)が互いに素であり、\(ca \equiv cb \,(\mathrm{mod}\,n)\)ならば、\(a \equiv b \,(\mathrm{mod}\,n)\)という整数の合同の性質があります。今回は、\(k\)と\(10\)は互いに素なので、\(k(a_{\ell}-a_{\ell^{\prime}})\equiv a_{\ell}-a_{\ell^{\prime}} \,(\mathrm{mod}\,10)\)で、チェックディジットが異なることが示されました。

ただし、チェックディジットは、すべての間違いを完全に検出できるわけではありません。モジュラス10・ウエイト1,3の場合は、1つの数字の誤り（single digit error）は100%検出できますが、完全には検出できないケースも存在します。

例えば、隣り合った番号\(16\)が\(61\)に入れ替わった場合（transposition error）は検出できません。チェックディジットの計算式の差は\((1+3\cdot 6)-(6+1\cdot 3)=10 \equiv 0\,(\mathrm{mod}\,10)\)で、差を区別できていません。（\(1,6\)の差が\(5\)であるのが悪い。差が\(5\)ではない、隣り合わった番号の入れ替えは検出できます。）

参考：Check digit – Wikipedia(en), チェック・ディジットによるエラー検出率の導出 – 吉田敬一

以上、バーコードやISBNのチェックディジットとは何か、計算例や原理を紹介してきました。

情報やコード（符号）を効率よく正確に伝えるための学問は、情報理論や符号理論と呼ばれており、誤りの検出と訂正（error detection and correction）はその主要なテーマとなっています。

バーコードやISBN、何かのIDカードなどの数字を見たら、チェックディジットのような人間の誤りを減らすための工夫がされているのだな、と思いだしてみると面白いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。