なぜ外積を考えるか平面の法線ベクトルの求め方

どうも、木村（@kimu3_slime）です。

ベクトルの外積\(a \times b\)の定義は、初めて見るとどうしてそんな形なのか疑問に思うこともあるでしょう。

今回は、平面の法線ベクトルを求める中で、その定義が自然と登場することを紹介します。

平面の法線ベクトルとは何か
法線ベクトルの求め方と外積
こちらもおすすめ

平面の法線ベクトルとは何か

3次元空間\(\mathbb{R}^3\)における平面をイメージしましょう。

平面には、その平面上の位置ベクトルと直交するベクトルが存在しますが、それを平面の法線ベクトル（normal vector to the plane）と呼びます。

具体的に、法線ベクトルを求めてみましょう。

\[ \begin{aligned}f_1(x,y)=2x-3y\end{aligned} \]とすると、そのグラフは平面で、

\[ \begin{aligned}2x-3y = z\end{aligned} \]

を満たす点\(p=(x,y,z)\)の集まりです。

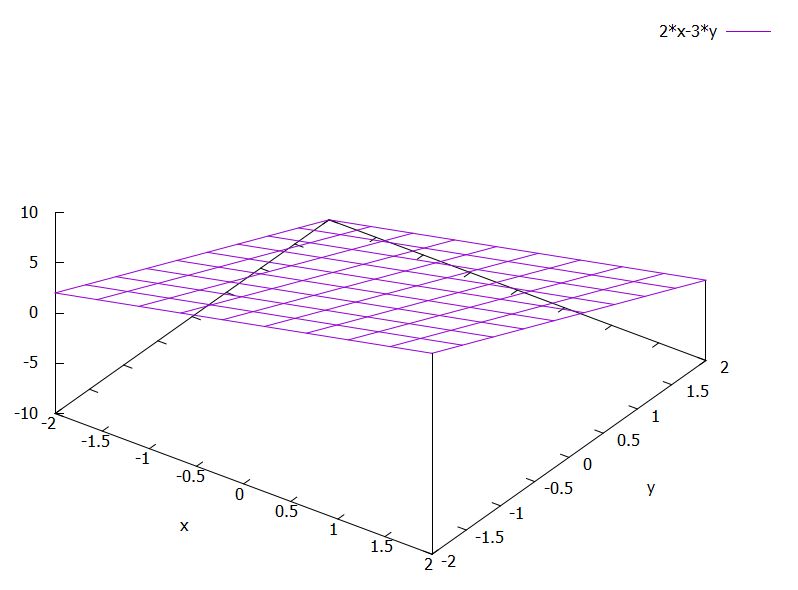
法線ベクトルを\(n= (n_1,n_2,n_3)\)と一般的に表して、平面と直交するという条件から具体的に求めてみましょう。

平面上の基準となる点を、\(p_0= (0,0,0)\)と選んでみます。さらに平面上の2つの点を、適当に、\(a = (1,0,2)\)、\(b =(0,1,-3)\)と選びましょう。2つの位置ベクトル\(a-p_0,b-p_0\)は線形独立です。

平面上の位置ベクトル\(a-p_0\),\(b-p_0\)と法線ベクトル\(n\)は直交しているので、その内積は0になります。

\[ \begin{aligned}\langle a-p_0,n \rangle =0,\langle b-p_0,n \rangle =0\end{aligned} \]

したがって、内積を計算すれば

\[ \begin{aligned}n_1+2n_3=0, n_2-3n_3 =0\end{aligned} \]

です。これを満たす\(n\)の例として、\(n=(-2,3,1)\)が得られました。

逆に、ベクトル\(n\)が与えられれば、\(n\)を法線ベクトルとして\(p_0\)を通る平面の方程式が定まります。

\(n=(-2,3,1)\)を法線ベクトルとして、\(p_0=(0,0,0)\)を通る平面の方程式を求めてみましょう。

その平面上の点を\(p=(x,y,z)\)とします。平面の位置ベクトル\(p-p_0\)と法線ベクトル\(n\)は直交するので、その内積は0です。

\[ \begin{aligned}\langle p-p_0,n \rangle =0\end{aligned} \]

したがって、

\[ \begin{aligned}-2x +3y +z =0\end{aligned} \]

と平面の方程式が求めらました。（さきほど見た平面と同一です）

一般に、\(ax+by+cz=d\)なる平面の法線ベクトルのひとつは、\(n=(a,b,c)\)です。（逆も同様）

ここまでは平面を考えましたが、一般に曲面\(f(x,y,z)=0\)の法線ベクトルを、接平面の法線ベクトルして考えることができます。点\((x_0,y_0,z_0)\)における接線の方程式は

\[ \begin{aligned}f_x(x-x_0)+f_y(y-y_0)+f_z(z-z_0)=0\end{aligned} \]

すなわち、法線ベクトルは勾配ベクトル\(n=\nabla f:=(f_x,f_y,f_z)\)となります。

法線ベクトルの求め方と外積

法線ベクトルを求める手順を一般化すると、外積の考え方にたどり着きます。

（原点を通る）平面は、（線形独立な）2つのベクトル\(a,b\)の線形結合として表わせます。

\(a=(a_1,a_2,a_3),b=(b_1,b_2,b_3)\)として、法線ベクトル\(n=(n_1,n_2,n_3)\)との直交条件を調べてみましょう。

\[ \begin{aligned}\langle a,n \rangle =0,\langle b,n \rangle =0\end{aligned} \]

\[ \begin{aligned}a_1 n_1+a_2 n_2 +a_3 n_3 =0\end{aligned} \]

\[ \begin{aligned}b_1 n_1+b_2 n_2 +b_3 n_3 =0\end{aligned} \]

1次元分の不定性がありますが、ガウスの消去法を用います。第2式の\(n_1\)の項を消去すれば、

\[ \begin{aligned}(b_2-\frac{b_1}{a_1} a_2 ) n_2 +(b_3-\frac{b_1}{a_1} a_3) n_3 =0\end{aligned} \]

\[ \begin{aligned}(a_1b_2-b_1 a_2 ) n_2 = – (a_1b_3-b_1 a_3) n_3 \end{aligned} \]

ここで、係数が共通するように\(n_3 =a_1b_2-b_1 a_2 \)としましょう。すると、\(n_2 = – (a_1b_3-b_1 a_3) \)です。

これらを使って\(n_1\)を求めれば、

\[ \begin{aligned}n_1 =(- \frac{a_2}{a_1})(-(a_1b_3-b_1 a_3))+\frac{a_3}{a_1}(a_1b_2-b_1 a_2)\\= a_2b_3 -a_3b_2\end{aligned} \]

となります。以上の結果を、\(a\)と\(b\)の外積（outer prodct）\(a\times b\)と呼び、

\[ \begin{aligned}n= \begin{pmatrix} a_2b_3 -a_3b_2\\ – (a_1b_3-b_1 a_3) \\ a_1b_2-b_1 a_2\end{pmatrix} =: a\times b\end{aligned} \]

と定めるわけです。

外積はひとつのベクトルを定めるので、ベクトル積とも呼ばれます。これに対して、内積はひとつのスカラーを定めるので、スカラー積とも呼ばれます。

ベクトル\(a,b\)に直交するベクトル（のひとつ）が、外積\(a \times b\)の計算によって求まります。直交するベクトル自体には1次元分の不定性がありますが、\(n_3 =a_1b_2-b_1 a_2 \)となるものを選んだわけです。

外積はもとのベクトルと直交すること、

\[ \begin{aligned}\langle a,a\times b \rangle =0,\langle b, a\times b\rangle =0\end{aligned} \]

は、議論を元に辿ればわかります（ぜひチェックしてみてください）。

\(n=a\times b\)のとき、そのノルムは一般には1とは限りません（\(\|a\times b\|= \|a\|\|b\|\sin \theta\)）。ただし大きさを1になるように揃えることはできて、\(n^{\prime} = \frac{1}{\|a\times b\|}a\times b\) を単位法線ベクトル（unit normal vector）と呼ばれます。

外積を用いれば、空間内の3点を通る平面の方程式も簡単に求められます。位置ベクトルの外積を計算して法線ベクトルを求めれば、そこから平面の方程式が得られるわけです。

また、より広く、ベクトル解析や微分幾何学に法線ベクトルや外積は登場します。例えば面積分、ガウスの発散定理、回転\(rot\)、曲率など。

外積の定義を忘れたり、納得できなかったりしたら、法線ベクトルの求め方をぜひ思い出してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。