どうも、木村(@kimu3_slime)です。
今回は、関数のなめらかさと微分可能性の関係、\(C^k\)級という用語について紹介します。
連続だが微分不可能な例
関数のなめらかさとは、感覚的に言えば、とがっている点がないことです。
逆にとがっていてなめらかでない関数の例としては、絶対値関数\(f_1(x)=|x|\)が挙げられます。

画像引用:WolframAlpha
この\(f_1(x)\)は、\(x=0\)においてとがっています。とがっているとはどういうことでしょうか? ……それは傾きが急激に変化していること、すなわち微分可能ではないことです。
\[ \begin{aligned}\lim_{h \searrow 0 }\frac{|0+h|-|0|}{h}=1\end{aligned} \]
\[ \begin{aligned}\lim_{h \nearrow 0}\frac{|0+h|-|0|}{h}=-1\end{aligned} \]
と、傾き(ニュートン商)の右側からの極限と左側の極限が一致しないので、微分可能ではありません。
\[ \begin{aligned}C^0 =C := \{f \mid f は連続\}\end{aligned} \]
\[ \begin{aligned}C^1 = \{f \mid f は微分可能で、f^{(1)}は連続\}\end{aligned} \]
と関数の集合(空間)を定義します。文字\(C\)を使うのは、連続性(continuity)の頭文字によるものでしょう。
一般に、微分可能な関数は連続なので、\(C^0 \subset C^1\)という包含関係があります。
絶対値関数\(f_1\)は連続ではあるが微分可能でない関数なので、\(f_1\in C^{0}\)ですが、\(f_1\notin C^1\)の例と言えます。
\[ \begin{aligned}f_2(x)= \begin{cases}0 & (x <0 )\\1 & (x\geq 1)\end{cases}\end{aligned} \]
と置けば、\(f_2\)は\(x=0\)において不連続です(ヘヴィサイドの階段関数)。つまり、\(f_2 \in C^{0}\)ですね。関数には、不連続なもの、連続なもの、微分可能なものと、さまざまなものがあります。
厳密な解析学が発展する前は、「連続な関数は、例外となる有限個の点を除きさえすれば微分可能である」と信じられていました。
定理9.1 (Amp`ereの定理,1806年)任意の関数は有限個の例外点を除いてすべての点では微分可能である.
参考:関数の歴史 – RIMS, Kyoto University – 京都大学
しかし、それは誤りであると後に判明します。
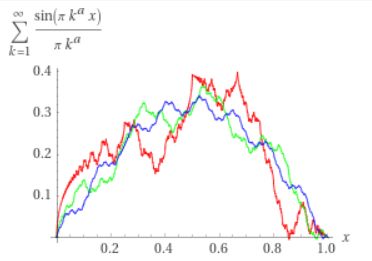
画像引用:WolframAlpha
(すべての\(x\)において)連続だが微分不可能なこの関数は、ワイエルシュトラス関数と呼ばれています。
この関数も、\(C^0\)に属するけれども\(C^1\)には属しない関数の例ですね。ものすごくギザギザはしていますが、連続でつながっている関数です。\(C^1\)級の関数を考えれば、このようなギザギザは除外されます。
C^k 級関数とは
では、連続微分可能な関数\(C^1\)は、完全になめらかなものなのでしょうか?
\[ \begin{aligned}f_3(x)= \begin{cases}-x^2 & (x <0 )\\x^2 & (x\geq 1)\end{cases}\end{aligned} \]
なる関数を考えます。
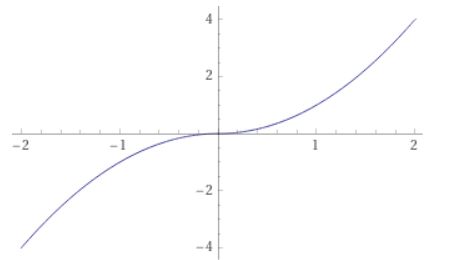
画像引用:WolframAlpha
\(x^2\)を原点で反転してつなぎあわせた関数ですが、\(x=0\)にちょっとした不自然さ、つぎはぎ感があります。
\(f_3\)は微分可能であり、導関数は\(f_3^{(1)}=2|x|\)です。つまり、1回導関数は連続ですが、2回微分可能ではない関数となっています。この2回微分可能でないという性質が、つぎはぎ感の要因だったのです。
一般に、次のような連続関数のなす集合(空間)を定義します。
\[ \begin{aligned}C^k = \{f \mid f はk 回微分可能で、f^{(k)}は連続\}\end{aligned} \]
\[ \begin{aligned}C^\infty = \{f \mid f は何回でも微分可能\}\end{aligned} \]
\(C^k, C^{\infty}\)に属する関数をそれぞれ、\(C^k\)級の関数、\(C^{\infty}\)級の関数と言います。\(C^k\)級の関数は\(k\)回連続微分可能(continuously differentiable)、\(C^\infty \)級の関数は、なめらかな関数(smooth function)と呼ばれます。
さきほどの関数は、\(f_3 \in C^1\)ですが\(f_3 \notin C^2\)となる例です。
任意の\(k\)に対して、\(C^k\subset C^{k+1}\)ですが、\(C^k\not\subset C^{k+1}\)です。\(C^k \)に属するが\(C^{k+1}\)に属さない関数の例はいつでも存在します。
\(C^\infty\)級の関数、なめらかな関数の例としては、多項式関数\(a_n x^n+\cdots+a_0\)やべき関数\(x^p\)、指数関数\(e^x\)、対数関数\(\log x\)、三角関数\(\sin x,\cos x\)といった関数があります。中学・高校数学でも学ぶこれらの有名な関数は、初等関数とも呼ばれるものです。
画像引用:WolframAlpha
数学や諸科学においては、「関数は適度になめらかなものとする」という仮定が置かれることがあります。それは、議論に必要となるだけの\(C^k\)級関数を考える、ということです。場合によっては、\(C^\infty\)を意味していることもあります。
強いなめらかさを課せば引き出せる性質は増えますが、一方で対象となる関数は当然減っていきます。今、関数\(f\)にはどれくらいの微分可能性を仮定しているかを考えるとき、\(C^k,C^\infty\)といった考え方は有効です。
さらに、無限回微分可能な関数の一部は、テイラー展開によってべき級数に展開できます。
\[ \begin{aligned}C^\omega := \{ f \mid 定義域の各点で f(x) = \sum _{k=0} ^\infty a_k x^k と表せる\}\end{aligned} \]
このような関数を、\(C^{\omega}\)級関数、解析的な関数(analytic function)と呼びます。さきほど挙げた初等関数は、\(C^\infty\)であるだけでなく、\(C^\omega\)にも属します。
一方で、すべてのなめらかな関数が、解析的であるわけではありません。例えば、
\[ \begin{aligned}f_4(x)= \begin{cases}0 & (x <0 )\\e^{-\frac{1}{x^2}} & (x\geq 1)\end{cases}\end{aligned} \]
とすると、\(f_4 \in C^\infty\)ですが、\(f_4 \notin C^{\omega}\)である(\(x=0\)で解析的でない)ことが示せます。
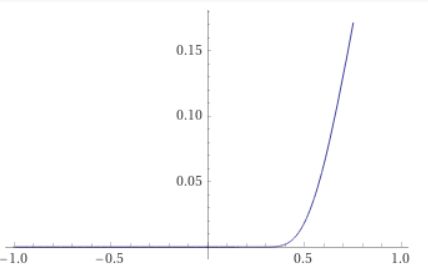
画像引用:WolframAlpha
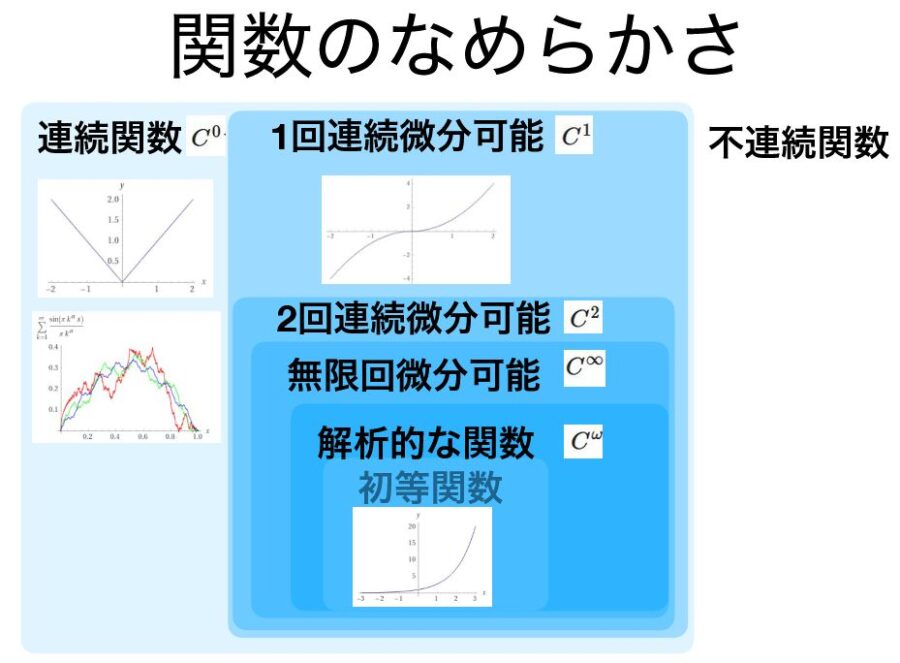
以上、とがった関数を例に挙げながら、関数のなめらかさ、\(C-k\)級関数といった呼び方を紹介してきました。
連続関数\(C^0\)や連続微分可能な関数のなす集合\(C^k\)といった記法は、微分可能性を簡潔に表すにあたり便利です。
フーリエ級数の理論を厳密に展開するときには、「どこまでの連続性(や可積分性)を持てば級数展開できるか?」という問いを考え、そこでもこの記法は有効です。
さらに、関数解析と呼ばれる分野では、このような関数のなす集合が線形空間として見れること、一般には無限次元であることを知るでしょう。
目の前に現れた関数がどれだけの連続性や微分可能性が持つか、この関数はどんな集合(空間)に住んでいるのか、という視点をぜひ身につけてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
共立出版 (1980-11-01T00:00:01Z)
¥5,390




