どうも、木村(@kimu3_slime)です。
今回は、複素数の積はある種の「回転」と見なせることを紹介します。
複素数平面と和・積の対応
複素数とは、2つの実数\(x_1,x_2\)と虚数\(i\)を使って、\(z= x_1+x_2 i\)と表せる数のことです。虚数は、\(i^2 =-1\)という関係を満たします。
ひとつの複素数\(z\)は、2つの実数\(x_1,x_2\)により決まるので、これを平面に表すことができます。このようにして複素数を表した平面は、複素数平面と呼ばれるものです。
複素数\(z=x_1+x_2 i,w=y_1+y_2 i\)の和、積は次のように定義されます。
\[ \begin{aligned}z+w = (x_1+y_1)+(x_2+y_2)i \end{aligned} \]
\[ \begin{aligned}zw = (x_1y_1- x_2y_2)+(x_1 y_2+x_2 y_1)i \end{aligned} \]
複素数の和は、実平面\(\mathbb{R}^2\)と同様、矢印の合成として見ることができます。
しかし複素数の積は、パッと見ではどういうものなのかわかりません。\(\mathbb{R}^2\)のベクトルには(複素数のような)積は定義されず、ここが複素数\(\mathbb{C}\)と2次元の実数\(\mathbb{R}^2\)の違いとなってきます。
簡単な例で考察してみましょう。
\(z=1\)は実軸上にあります。これに\(i\)をかけると、虚軸に写ります。さらに\(i\)をかけると、\(i^2 =-1\)と実軸に戻ってきます。
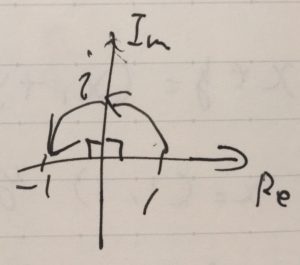
\(i\)をかけるという操作を、複素数平面上に図示しました。すると、\(i\)はあたかも点を時計回りに90度回転させているように見えます。2回かければ180度、4回かければ360度してもとに戻ってきます\(i^4 =1\)。
このとき、\(R_{\frac{\pi}{2}}= \begin{pmatrix} 0& -1\\ 1 & 0 \end{pmatrix}\)という90度の回転行列を考えてみましょう。
すると、\(R_{\frac{\pi}{2}}R_{\frac{\pi}{2}}= \begin{pmatrix} -1& 0\\ 0 & -1 \end{pmatrix}=-I\)です。これは\(i^2 =-1\)に対応する式です。
\[ \begin{aligned}1\leftrightarrow I, \quad i \leftrightarrow R_{\frac{\pi}{2}} \end{aligned} \]
\[ \begin{aligned}i^2=-1 \leftrightarrow R_{\frac{\pi}{2}}R_{\frac{\pi}{2}} =-I \end{aligned} \]
複素数と回転行列には、何か対応関係がありそうな気がしてきました。
複素数の積=回転行列の積の対応関係
複素数には、極形式という表し方があります。
\(z\)の大きさを\(r\)、\(z\)が実軸となす角(偏角)を\(\theta \)として、\(z= r (\cos \theta + i \sin \theta)\)です。オイラーの公式\(e^{i\theta}=(\cos \theta + i \sin \theta)\)を使えば、\(z= r e^{i\theta}\)と簡単に表せます。例えば、\(i = 1\cdot e^{\frac{\pi}{2} i }\)です。
(複素指数関数に関するオイラーの公式は、別記事で紹介予定)
一方で、\(\theta\)だけ回転させる行列は、\(R_\theta = \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix}\)でした。
これは大きさ1(\(|z|=r=1\))の複素数と一対一に対応しています。
\[ \begin{aligned}R_\theta = \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix} \leftrightarrow e^{i\theta}\end{aligned} \]
\(\mathbb{R}^2\)上で\(R_\theta\)をかけることは、\(\mathbb{C}\)上で\(e^{i\theta}\)をかけることに対応しています。
\(x=(x_1,x_2)\in \mathbb{R}^2\)として、\(z=x_1 +x_2 i\)となる複素数を\((x_1,x_2)\)に表すのが複素数平面でした。
\[ \begin{aligned} R_\theta x &= \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix} \begin{pmatrix} x_1 \\ x_2\end{pmatrix} \\ &=\begin{pmatrix} x_1\cos \theta -x_2 \sin \theta \\ x_1 \sin \theta +x_2 \cos \theta \end{pmatrix}\end{aligned} \]
\[ \begin{aligned} e^{i\theta} z &= (\cos \theta + i \sin \theta)(x_1 +x_2 i)\\ &= (x_1\cos \theta -x_2 \sin \theta) +(x_1 \sin \theta +x_2 \cos \theta )i \end{aligned} \]
ときちんと対応しています。
また、角度\(\alpha\)と角度\(\beta\)の回転をあわせたものは、\(\alpha+\beta\)の回転になるという性質が、回転行列にはありました。
\[ \begin{aligned}R_\beta R_\alpha = R_{\alpha +\beta}\end{aligned} \]
それぞれを複素数で表せば、\(z= e^{i\alpha},w=e^{i \beta}\)として、
\[ \begin{aligned}zw= e^{i\alpha}e^{i \beta}= e^{i(\alpha +\beta)}\end{aligned} \]
という関係です。これは指数関数の法則として、複素数の世界でも成り立つものです。
以上でわかるように、複素数の積は、\(z=r e^{i \theta}\)と極形式で表すと、幾何学的に捉えやすいです。
まず、\(e^{i \theta}\)をかけることは、複素数平面上の角度\(\theta\)の回転を意味します。そして、それに\(r\)をかけることは、\(r\)倍の拡大縮小を意味します。つまり、複素数の積をかけることは、ある点を\(r\)倍だけ拡大縮小し、\(\theta\)だけ回転させることを意味することがわかりました。
(ちなみに、複素共役を取ること\(\overline{z} =x_1-x_2i\)は、実軸に関する反転\(\begin{pmatrix} 1& 0\\ 0 & -1 \end{pmatrix}\)と見ることができます。確かめてみてください。)
(大きさ1の複素数の集合\(\mathbb{T}:= \{z \in \mathbb{C} \mid |z| =1\}\)は、複素数の積について群をなし、円周群 circle group と呼ばれています。また、2次の回転行列のなす群は、回転群、特殊直交群\(SO(2)\)と呼ばれているのでした。\(f:\mathbb{T} \to SO(2) \)を、\( e^{i\theta} \mapsto \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin\theta & \cos \theta \end{pmatrix} \)で定めると、今回示したことにより\(f\)は同型写像です。つまり、円周群と2次回転群は同型 \(\mathbb{T} \simeq SO(2)\)です。)
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説
以上、複素数の積と回転行列の対応関係を紹介してきました。回転行列の固有値には複素数\(e^{i\theta},e^{-i\theta}\)が登場しますし、複素数の積は回転行列に対応させることができます。
回転操作と複素数、三角関数と複素指数関数には、何かしらの縁があるという視点を得てもらたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥8,800
岩波書店 (2003-12-12T00:00:01Z)
¥2,640