置換行列とは？置換との関係、性質、転置・直交行列

どうも、木村（@kimu3_slime）です。

置換行列は、ベクトルを入れ替える行列で、可逆行列のシンプルな例として頻繁に登場します。いくつかのものを入れ替える操作＝置換は、数学全般で登場するアイデアで、慣れ親しんでおきたいものです。

今回は、置換行列とその性質、置換との関係、転置行列と直交行列について紹介したいと思います。

置換行列とは
置換行列と置換との対応
置換行列の性質
こちらもおすすめ

置換行列とは

線形代数学では、置換行列というものを扱います。

例えば、\( \begin{pmatrix} 0& 1\\1 & 0 \end{pmatrix}\)は置換行列です。なぜ置換と呼ばれるかというと、他のベクトル・行列との積を取ると、その中身を入れ替えるからです。

\( \begin{pmatrix} 0& 1\\1 & 0 \end{pmatrix}\begin{pmatrix} x_1\\x_2 \end{pmatrix}=\begin{pmatrix} x_2\\x_1 \end{pmatrix} \)

\( \begin{pmatrix} 0& 1\\1 & 0 \end{pmatrix}\begin{pmatrix} a& b\\c & d \end{pmatrix}=\begin{pmatrix} c& d\\a & b \end{pmatrix} \)

\( \begin{pmatrix} a& b\\c & d \end{pmatrix}\begin{pmatrix} 0& 1\\1 & 0 \end{pmatrix}=\begin{pmatrix} b& a\\d & c \end{pmatrix} \)

\( \begin{pmatrix} 0& 1&0\\1 & 0&0 \\ 0&0&1 \end{pmatrix}\)や\( \begin{pmatrix} 0& 1&0\\0 & 0&1 \\ 1&0&0 \end{pmatrix}\)も置換行列です。

置換行列は、行列の基本変形を表す基本行列の一種として、線形方程式を解くための方程式や変数の入れ替え操作を表します。

参考：線形方程式の解き方：ガウスの消去法と基本変形・ランク、LU分解

少し一般的に表しましょう。

\(e_i\)を第\(i\)成分が1、他の成分が0の縦ベクトル（単位ベクトル）とします。このとき、\(e_1,\dots,e_N\)の異なる\(N\)個を並べてできる行列\(P\)を、\(N\)次の置換行列（permutation matrix）と呼びます。

\(\begin{pmatrix} 0& 1\\1 & 0 \end{pmatrix}=(e_2,e_1)\)、\( \begin{pmatrix} 0& 1&0\\1 & 0&0 \\ 0&0&1 \end{pmatrix}=(e_2,e_1,e_3)\)、\( \begin{pmatrix} 0& 1&0\\0 & 0&1 \\ 1&0&0 \end{pmatrix}=(e_3,e_1,e_2)\)なので置換行列です。単位行列\(I= (e_1,e_2,e_3)\)もまた、単位行列。

この定義によれば、\((e_1,e_1)\)や\((e_1,e_2+e_1)\)は置換行列ではありません。異なる単位ベクトルを並べていないとダメですし、足し合わせれば単なる入れ替えではなくなってしまいます。

置換行列と置換との対応

置換行列は、置換という概念に対応しています。

置換とは、並んだ記号の入れ替え操作です。

例えば、\((1,2,3)\)と並んだ数字を\((3,1,2)\)と並べ替える操作を考えましょう。その操作を\(f\)と関数（写像）で表すならば、\(f(1)=3,f(2)=1,f(3)=1\)という対応規則です。

この対応規則は、二行で書き下すことができます（二行記法）。上の行の行き先が、下の行に対応するという読み方です。表記は同じですが、行列とは別物ですので注意してください。

\[ \begin{aligned}f=\begin{pmatrix} a & b & c\\ c& a& b \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}\end{aligned} \]

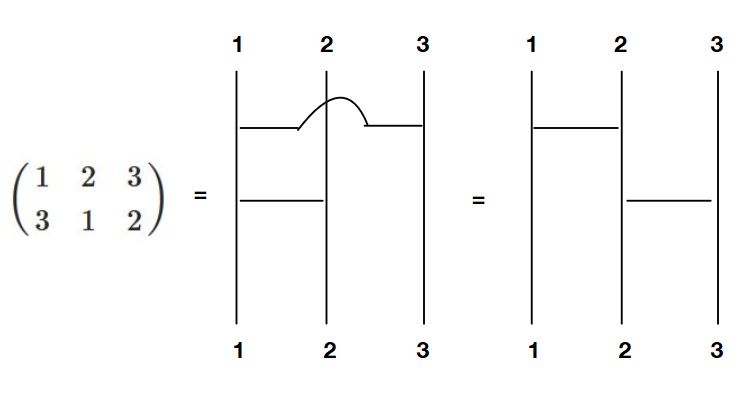
一般に\(N\)次の置換（permutation）とは、有限集合\(X=\{1,\dots,N\}\)から\(X\)それ自身への全単射のことです。文字列\(1,\dots,N\)の並び替えと言っても良いでしょう。全単射とは、すべての数字が行き先になっていて（全射）、異なる入力が異なる出力に対応していること（単射）です。

\(N\)次の置換全体の集合は、置換群、または対称群\(S_N\)と呼ばれています。

置換について詳しくは：対称群の基礎：置換・互換の記法、符号、交代群を解説

置換行列と置換には、対応関係があります。

例えば、置換行列\( \begin{pmatrix} 0& 1&0\\0 & 0&1 \\ 1&0&0 \end{pmatrix}=(e_3,e_1,e_2)\)は、次のように単位ベクトルを入れ替えています。\((e_3,e_1,e_2)e_1=e_3\)、\((e_3,e_1,e_2)e_2=e_1\)、\((e_3,e_1,e_2)e_3=e_2\)といったように。つまり、これは置換\(f=\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}\)に対応しています。

より一般に、置換行列\(P\)は、\(Pe_i = e_{f(i)}\)となる置換\(f\)に対応しています。逆に言えば、置換\(f\)が与えられたとして、\(Pe_i = e_{f(i)}\)を満たす行列\(P\)は置換行列です。

（行列\(P\)の成分を\(p_{ij}\)として、\(p_{ij}=\delta _{if(j)}\)と定めるとも言える。ここで\(\delta \)は添字\(i,j\)が異なれば0、同じなら1を返す関数で、クロネッカーのデルタと呼ばれる。）

以降では、置換\(f\)によって定まる置換行列を、\(P_f\)と書くことにしましょう。

何も入れ替えない置換\(e=\begin{pmatrix} 1 & 2 & 3\\ 1& 2& 3 \end{pmatrix} \)は恒等置換と呼ばれます。恒等置換による置換行列は、単位行列\(P_e =I\)です。

置換行列の性質

置換行列の性質を簡単に紹介しましょう。

置換行列の積は、置換の積

\(f,g\)を置換として、\(P_g P_f = P_{g\circ f}\)

任意に選んだ単位ベクトル\(e_i\)について、両辺で送った先が同じなら、両辺の行列は等しいと言えます。

\(P_g P_f e_i =P_g e_{f(i)} =e_{g(f(i))}\)であり、\(P_{g\circ f} e_i =e_{g\circ f (i)}=e_{g(f(i))}\)なので、両辺は等しいと言えました。

この計算により、置換行列同士の積もまた置換行列です。置換と置換の合成\(g\circ f\)は、置換の積とも呼ばれ、ときに\(\circ\)の記号は省略されます。置換行列の積と、置換の積はうまく両立したものになっているわけです。（群論の言葉で言えば、対称群から行列群への単射な準同型写像が存在する）

参考：群論入門～回転群と巡回群を例に、群の定義・同型・位数を解説

行列式は符号に対応する

\(\det P_f = \mathrm{sgn}f\)

ただし、\(\mathrm{sgn}f\)は置換\(f\)の符号です。つまり、置換行列の行列式は、\(1\)か\(-1\)となります。

参考：対称群の基礎：置換・互換の記法、符号、交代群を解説

置換において、2つの要素だけを入れ替えて他を入れ替えないものを互換と呼びます。すべての置換は互換の積として表わせ、そこに現れる互換の個数によってその置換の符号が決まるのでした。

つまり、置換\(f\)に互換をかけていって、\(g\circ f=e\)とできます。これは積の対応により、置換行列を単位行列に変形できる\(P_g P_f= P_e=I\)ということです。行列式の性質により、\((\det P_g) (\det P_f)=1\)です。

一般に行列式は、ある列とある列を1つ入れ替えると\(-1\)倍されます（交代性）。そして、\(g\)は列の入れ替え：互換の積であり、その入れ替え回数は\(f\)の符号に等しいです。よって、\(\mathrm{sgn}f (\det P_f)=1\)、すなわち\(\det P_f = \mathrm{sgn}f\)が示せました。

参考：行列式の導出と定義、性質、計算方法（余因子展開）

例えば、置換行列\( \begin{pmatrix} 0& 1&0\\0 & 0&1 \\ 1&0&0 \end{pmatrix}=(e_3,e_1,e_2)\)は、2回の列の入れ替えで単位行列になるので、\(\det P = (-1)^2=1\)です。

一方で、対応する置換は、次のような互換に分解できます。\(\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix}=\begin{pmatrix} 2 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 \end{pmatrix}\)。なので、\(\mathrm{sgn}\begin{pmatrix} 1 & 2 & 3\\ 3& 1& 2 \end{pmatrix} =1\)です。

逆行列が転置行列となる：置換行列は直交行列

置換行列の行列式は0ではないので、置換行列は可逆です。つまり逆行列が存在します。

\((P_f) ^{-1}= (P_f) ^{\top}\)

ここで\(P^{\top}\)は\(P\)の転置行列です。一般に行列\(A=(a_{ij})\)の転置行列は、\(A^{\top}=(a_{ji})\)と行と列を入れ替えた、対角成分について折り返した行列と定義されます。

逆行列の定義より、\((P_f) ^{\top} P_f = I\)を示せば良いわけです。

まず、置換行列\(P_f\)に対して、\(P_f^{\top}=P_{f^{-1}}\)となります。\(f^{-1}\)は置換\(f\)の逆置換（逆関数、逆写像）です。置換行列の成分は\(p_{ij}=\delta _{if(j)}\)だったので、その転置の成分は\(\delta _{f(j) i}\)ですが、\(\delta _{f(j) i} =\delta _{j f^{-1}(i)}\)です。\(f\)は全単射なので、\(f(j)=i\)であることと、\(j=f^{-1}(i)\)であることは同値なので。

続いて、置換行列の定義より、\(P_{f^{-1}} P_f e_i = P_{f^{-1}} e_{f(i)}= P_{(f^{-1}(f(i)))}=e_i\)です。したがって、\(P_{f^{-1}} P_f=I\)が成り立ちます。\(P_f^{\top}=P_{f^{-1}}\)と合わせて\((P_f) ^{-1}= (P_f) ^{\top}\)が得られました。

一般に、逆行列が転置行列になる \(X^{-1}=X^{\top}\) 行列\(X\)を直交行列（orthogonal matrix）と言います。

直交行列の行ベクトル（列ベクトル）は、直交していて、その大きさが1です。また、直交行列の行列式は1か-1になることが知られています。

置換行列はすべて直交行列ですが、すべての直交行列が置換行列であるわけではありません。例えばある種の回転行列\(\begin{pmatrix} \cos \frac{\pi}{4}& -\sin \frac{\pi}{4}\\ \sin \frac{\pi}{4} & \cos \frac{\pi}{4} \end{pmatrix}\)は、直交行列ではありますが置換行列ではありません。