応用のために測度論・ルベーグ積分論から学ぶのは正解か？

どうも、木村（@kimu3_slime）です。

よく、統計学、経済学、プログラミング、物理学を学ぶにあたり、その基礎的な数学として、測度論・ルベーグ積分論を学びたいという話を耳にします。

例えば、集合論→位相空間論→測度論・ルベーグ積分論→確率論→統計学、といったように、基礎→応用のように学んだほうが良い、という話が出てきます。

今回は、数学そのものを専門としたい人以外（数学のユーザー）にとっては、基礎→応用は必ずしもベストではない、別の学び方がある、という話をしていきたいと思います。

基礎から厳密に学ぶのは時間がかかる
測度論・ルベーグ積分論から学ぶのはハード
数学のユーザーは、厳密さより応用の価値が高い
こちらもおすすめ

基礎から厳密に学ぶのは時間がかかる

まず一般に、大学数学をガチガチに基礎から学ぶのにはものすごく時間がかかります。（どこまでを基礎と呼ぶかによりますが）

数学を探求したくて、数学に人生を捧げたいならそれで良いと思います。（そういう人は大学の数学科で学びましょう）

そうではなく、数学のユーザーならば、多少の厳密さは留保・放棄して、自分の興味ある応用や先端の分野に触れることをおすすめします。そして、必要に応じて基礎に戻って学べば良いのです。必要性がわからないまま基礎固めをしようとしたら、深い森から帰ってこれなくなります。（趣味的に基礎を学びたいなら、それはそれで良いです）

例えば、このロードマップにしても、そのすべてを基礎学問だと言って学び始めたら、キリがありません。

引用：大学数学のロードマップ～分野一覧と学ぶ順序

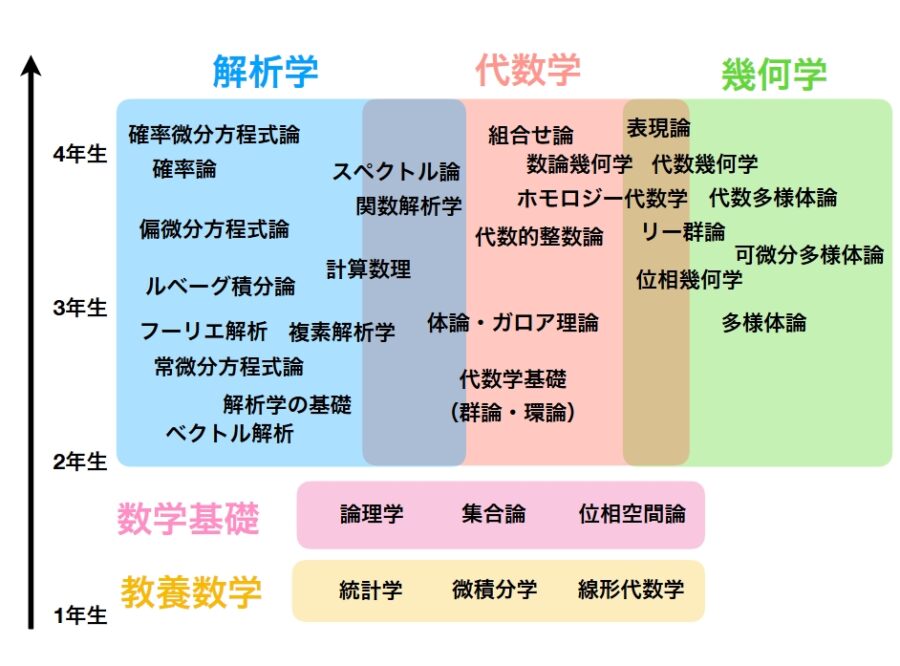
しっかりと数学を身につけたいならば、基礎・一般論から学んだほうが、最終的に速く理解が進むような内容があるのは確かです。

非数学の人にとっては、論理・集合、微積、線形あたりで十分はないでしょうか（数学科の人なら、そこに代数の初歩と、位相空間論が加わります。）。理工系の学部の1年次でだいたい学ぶのはこのあたりです。あとは、自分の専門を探求していく中で、必要に応じて数学にあたれば良いでしょう。

測度論・ルベーグ積分論から学ぶのはハード

もう少し具体的な話をします。統計学を基礎から勉強したくて、確率論を学びたくて、確率論の理解のために測度論が必要で、だから測度論から学ぶ……という学び方はおすすめしません。

当たり前のことかもしれませんが、統計学を学びたいなら統計学の教科書を読みましょう。測度論が求められるほど、高度な確率論は必要ないケースもあるでしょう（数理統計学を専門としているなら、そういう勉強も必要になるでしょうが）。高校レベルの確率の知識でだいたい足ります。それより、線形代数、多変数の微積分の扱いを知っておく方が役立つでしょう。

金融や経済のために、確率論を学びたい方も、すぐさま測度論から学ばなければならないということはないと思います。

シンクタンクに勤める私の大学時代の物理学科の友人は「ブラック－ショールズ方程式なんて2分で説明できる」とうそぶいている．彼はもちろん純粋数学は知らない．（物理が分かっているかも怪しい．）ただ，彼は勘がいいので，多分，ブラック－ショールズ方程式の本質は理解しているのだろう．

引用：大学で学ぶ数学は実社会で必要か ̶ ̶測度論的確率論を例にとって

こういう理解の仕方が最終的に良いかというと疑問ではありますが、現実的にはある程度基礎をすっ飛ばしてでも、応用について知っておくのは大事なことだと思います。

僕は大学の数学科で学んでいた時、測度論・ルベーグ積分論をやったのちに確率論の講義がありました。しかしその講義は、公理的確率論から中心極限定理程度までで、確率過程やブラック・ショールズ方程式の話までは入っていません。論理的な順序を重視すると、どうしても応用まで手につかないということは、数学科的な学びによくありがちです。（僕個人としてはそれはどうかと思う部分があります）

僕自身、測度論・ルベーグ積分論は数学のユーザーとして学んだ部分があります。

伊藤「ルベーグ積分入門」は昔からルベーグ積分の教科書として使われている本で、最初に手に取りました。これは1から読んでいくのは相当しんどい本だと思います。単純に、定義がレイアウト上見づらく、証明がみっちり書かれているので、何が重要なのかわかりづらいと思いました。

そしてこのとき、吉田「ルベーグ積分入門―使うための理論と演習」に出会い、使えるようになることは大事だなという視点を得ます。測度論は、関数解析と合わせて学び、1周目はサクッと済ませる感じで学びました。僕が専門的に学んでいきたかった偏微分方程式や力学系の本を読む中で、必要に応じて戻る感じで測度論や関数解析を学んでいきました。

結局、関数解析でも確率論でも偏微分方程式でも、収束定理の扱い、ほとんど至るところの意味、関数空間\(L^p\)とそこでの収束の意味がわかっていれば、読むのに支障はないのではないでしょうか。それを掴むのに、測度論を厳密に学ぶ必要はそれほどないと思います。（むしろ、線形代数の延長として、関数解析を学ぶ応用上の価値は高いと思います。僕にとって測度論やルベーグ積分論は、関数解析を実行する基礎・道具であるという見方をしています。ただ、何に大きな価値を置くかはその人の専門性の選び方次第でしょう。）

参考：なぜルベーグ積分を学ぶのか偏微分方程式への応用の観点から

応用を知らずに、一般論を最初に厳密に学ぶのは、時間を食う割には得られるものが少ないと僕は思っています。基礎理論を知っておくのがどれだけ必要かは、興味や身につけたい専門性によるのではないでしょうか。基礎と応用を往復しながら学ぶのが良いでしょう。

ただ、基礎理論を知ること自体は、効率が悪いかもしれませんが、損ではないと思います。役に立たないかもしれないけど学びたいという好奇心は、あるならば大事にしてください。僕自身も面白いと思った経験はあります。ルベーグ積分論では優収束定理がひとつの目標とされますが、それは単調収束定理、積分の単調性、測度の単調性から導かれている……という視点を得たときは、非常に頭の中がすっきりとしたものです。これも応用（収束定理）を知ってから基礎（測度や積分の定義）を見直すという視点なのかもしれません。

数学のユーザーは、厳密さより応用の価値が高い

というわけで、数学を専門とせず、何か自分の専門や応用を持っている人は、必ずしも基礎、測度論・ルベーグ積分論から始める必要はないという話をしてきました。仮に測度論を学び始めるにしても、論理・集合、微積、線形代数くらいの数学が身についていないと、教科書を読むのが大変だと思います。

数学専攻の人や教科書では、厳密な定義を使って、基礎的な定理を示すことが第一優先されています。理論を構築することそのものが目標にあるのです。教科書の書き方も、数学を利用する人向けというより、数学専攻向けといった趣の、高度で一般的な内容を書こうとしたものが多いです。応用を意識した数学の教科書は少ないです。

一方でそのような価値観は、数学の応用には必ずしも役立ちません。一般論や原理をよく理解していることは、それを具体的に運用できることにはつながらないのです。

非数学の人で、数学を応用したいと考えている人は、定理・手法を知った上で、具体的な問題へ応用・実装するスキルの方が大事だと思っています。

もしそんな応用をしていく中で、数学的な基礎が学びたくなったら、ぜひ学んでみてください。実践を伴った上で、基礎を学んで、また実践に戻って……という繰り返しの中で学ぶことは多いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。