どうも、木村(@kimu3_slime)です。
今回は、線形写像の核とは何か、線形方程式との関係を交えながら解説します。
線形方程式Ax=bの解とAx=0の解の関係
線形方程式の中には、解がただひとつに定まるものもあれば、無数の解を持つ(不定性を持つ)ものもありました。後者の例を見てみましょう。
\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 2 \end{pmatrix}\)
\(A:=\begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} ,b:= \begin{pmatrix} 1\\ 2 \end{pmatrix}\)
\(Ax=b\)のひとつの解は、\(v:=(1,0)\)です。しかし、\(Ax=b\)のすべての解がこれで求められたわけではありません。
他の解を探すために、\(Ax=0\)の\(x=0\)以外の解(非自明な解)を調べてみましょう。すると、\(c\)を実数として、\(w:=(c,c)\)は\(Ax=0\)の解であることがわかります。
このとき、\(v+w\)もまた、\(Ax=b\)の解となることがわかります。なぜなら、\(A(v+w)=Av+Aw=b+0 =b\)を満たすからです。(\(A\)の線形性\(A(v+w)=Av+Aw\)に注意しましょう)
この考察からわかるのは、\(Ax=b\)の解すべてを求めるためには、\(Ax=0\)の解がどれだけあるか調べる必要があるということです。
もし、\(Ax=0\)の解が\(x=0\)のみならば、\(Ax=b\)の解は唯ひとつです。しかし、\(Ax=0\)が\(x=0\)以外の解を持つならば、それだけ解の候補は広がり、定まらなさ=不定性が生じることがわかります。つまり問題は、\(Ax=0\)を満たす\(x\)はどういうものか、ということです。
定数項が\(0\)である線形方程式\(Ax=0\)は、斉次方程式、同次方程式(homogeneous equation)と一般に呼ばれています。(名前自体を覚える必要はないと思います)
線形写像の核とは何か
というわけで、\(Ax=0\)を満たす\(x\)の集合を、線形写像\(A\)の核、カーネル(kernel)と呼びます。
\[ \begin{aligned}\mathrm{Ker}A := \{x\in \mathbb{R}^N \mid Ax=0\}\end{aligned} \]
核は零空間(nullspace)\(N(A)\)とも呼ばれます。
さきほどの例で核を求めてみましょう。
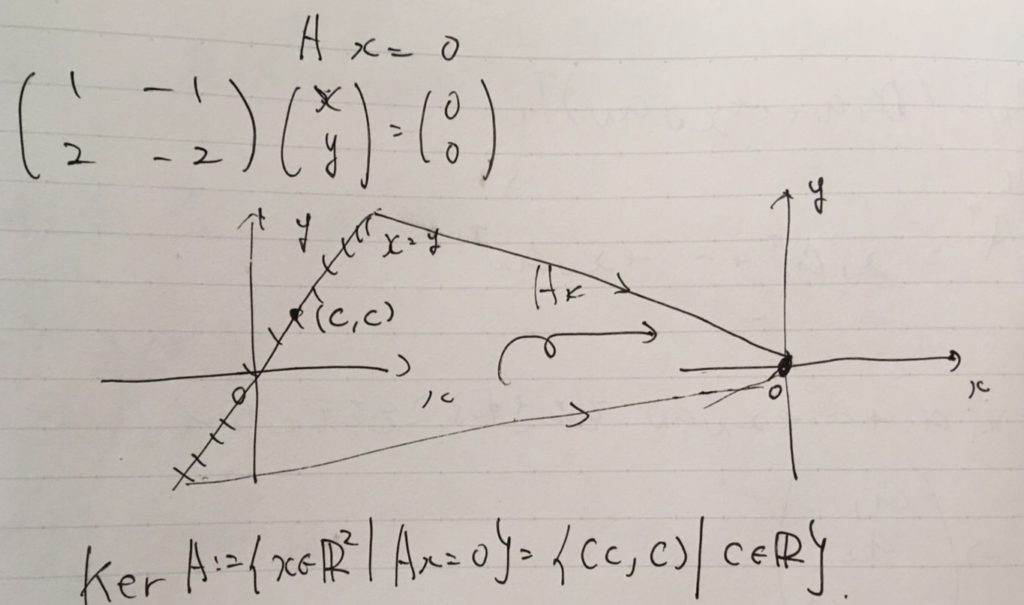
\(Ax=(x-y)(1,2)\)なので、\(x=y\)を満たす点が核に含まれます。したがって、
\[ \begin{aligned}\mathrm{Ker}A = \{x\in \mathbb{R}^N \mid Ax=0\}= \{(c,c)\mid c \in \mathbb{R}\}\end{aligned} \]
となります。\(Ax=b\)の解\(v\)に、どんな\(w \in \mathrm{Ker}A\)を加えても、\(v+w\)は\(Ax=b\)を満たしているのです。図を見ると、線形写像の核は、それがどれだけ多くの点\(x\)を\(0\)というただ1点に押しつぶしているかを測っていることが読み取れます。
核の性質
\(A\)を任意の線形写像とするとき、その核は必ず線形部分空間となります。
なぜか。\(p,q \in \mathrm{Ker}A, c\in \mathbb{R}\)としましょう。
\(A(p+q)= Ap+Aq =0+0=0\)なので、\(p+q \in \mathrm{Ker}A\)です。また、\(A(cp)= cAp =c0=0\)なので、\(cp \in \mathrm{Ker}A\)です。よって、\(\mathrm{Ker}A\)は線型部分空間。(\(A(p+q)= Ap+Aq,A(cp)=cAp\)が成り立つのは、\(A\)の線形性によるものです)
特に、\(A0=0\)なので、常に\(0 \in \mathrm{Ker}A\)です。0は常に含まれますが、それ以外に要素を持つかは\(A\)に依存します。
\(A\)の像\(A(\mathbb{R}^N ):= \{\ b \in \mathbb{R}^M \mid \exists x ( Ax =b ) \}\)も、同じく線形空間ですが、像は\(A\)による\(x\)の行き先であり、値域\(b \in \mathbb{R}^M\) の部分空間であることに注意しましょう。核は、\(A\)の定義域\(x\in \mathbb{R}^N\)の部分空間です。
ちなみに、像は一般の写像について定義されますが、核は線形写像(一般に準同型写像)に対してのみ定義されます。核の定義には、基点\(0\)が使われていて、何らの代数的構造(ここでは線形空間)が前提にあります。
参考:実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
核は線型部分空間であることから、そこには基底、次元が定まります。
さきほどの例では、\(\mathrm{Ker}A = \{(c,c)\mid c \in \mathbb{R}\}\)で、基底は\((1,1)\)で、1次元です。だから、一般の解には、\(c\)というパラメータによって表される1次元分の不定性があったわけです。
もし\(\mathrm{Ker}A = \{0\}\)となる問題を考えれば、そこに不定性はなく、解は一意に定まっています。
線形写像の核の次元は、退化次数(nullity)とも呼ばれます。さきほどの例では、線形方程式は1本分意味をなしておらず、すなわち1次元分退化していると言えるわけです。
実は、\(r\)を\(A\)のランクとして、\(\mathrm{dim} (\ker A) = N-r\)という式が成り立つことが知られています。線形写像の像の次元は、ランクとも等しいことから、
\[ \begin{aligned}\mathrm{dim} (\ker A) + A(\mathbb{R}^N) = N\end{aligned} \]
とも。これは次元定理、階数・退化次数の定理と呼ばれる定理です。(これについては、別記事で紹介予定)
ここまで見てきたことで予想されるように、核が自明=1点集合=\(\mathrm{Ker} A =\{0\}\)ならば、\(A\)は良い性質を持ちます。
(1) \(\mathrm{Ker} A =\{0\}\)であることは、次の主張と同値である。
(2) \(Ax=0\)の解は自明なもの(\(x=0\))のみである。
(3) 線形方程式\(Ax=b\)の解は一意的に定まる。
(4) 線形写像\(A\)は単射である。
(1),(2)は、核の定義による言い換えです。核とは\(Ax=0\)の解からなる集合で、それが\(x=0\)のみであるケースを考えています。
(2)から(3)を示します。(3)とは、\(x_1,x_2\)を\(Ax=b\)の解とするとき、\(x_1=x_2\)が導かれることです。\(Ax_1 =Ax_2\)と仮定しましょう。このとき、線形性より\(A(x_1-x_2)=0\)なので、\(x_1- x_2 \in \mathrm{Ker}A\)です。(1)より、\(x_1- x_2=0\)、すなわち\(x_1=x_2\)が言えました。\(Ax_1 =Ax_2\)ならば\(x_1=x_2\)とは、(4)写像の単射性の定義そのものです。
(3)から(2)を示します。\(x\)を\(Ax=0\)の任意の解とします。\(A\)の線形性より、\(A0=0\)です。つまり\(0\)も解です。(3)より解は一意だったので、\(x=0\)でなければなりません。よって、解は自明解のみとなります。
参考:無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法
\(\mathrm{Ker} A =\{0\}\)であり、\(v_1,\dots,v_k\)が線形独立ならば、\(Av_1,\dots, Av_k\)も線形独立である。
なぜか。\(Av_1,\dots, Av_k\)の線形独立性を確かめるため、\(c_1,\dots, c_k \in \mathbb{R}\)として、
\[ \begin{aligned} c_1 Av_1 + \cdots + c_k Av_k=0\end{aligned} \]
としましょう。\(A\)の線形性より、
\[ \begin{aligned} A(c_1v_1 + \cdots + c_k v_k)=0\end{aligned} \]
なので、\(c_1v_1 + \cdots + c_k v_k \in \mathrm{Ker} A\)です。仮定\(\mathrm{Ker} A =\{0\}\)より、\(c_1v_1 + \cdots + c_k v_k=0\)が成立する。\(v_1,\dots,v_k\)が線形独立だったので、\(c_1 =\cdots = c_k =0\)。よって、\(Av_1,\dots, Av_k\)は線形独立であることが言えました。
\(\mathrm{Ker} A =\{0\}\)のときは、\(A\)は線形独立性を保存するような写像となっているわけです。こういう行列を、一般に正則行列と言います。
(正則行列については、別の記事で紹介予定)
以上で、線形方程式\(Ax=b\)の解と\(Ax=0\)の解の関係、核\(\mathrm{Ker}A\)の定義とその性質について紹介してきました。
線形写像の核は、像に比べるとイメージしづらいものかもしれません。それは\(A\)による潰し具合を表すもので、核の次元は像の次元と補い合う関係になっています。核が1点集合のときは、線形方程式は一意な解を持ちます。
線形方程式の解の不定性を調べるために、核を調べるという視点が役立つことを、感じ取ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥8,800
東京大学出版会 (1966-03-31T00:00:01Z)
¥2,090
こちらもおすすめ
実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法