どうも、木村(@kimu3_slime)です。
フェルマー予想、ポアンカレ予想、リーマン予想……といった有名な予想は、数学を専門としていない方でも耳にしたことがあるかもしれません。2010年代に入ってから、日本の数学者が解決したとして話題になっているのが、abc予想。
そんなabc予想の解説本である「ABC予想入門」を紹介します。記事執筆時点では、読み放題サービスKindle Unlimitedの対象となっています。
abc予想とは
「ABC予想入門」は、abc予想をやさしく解説しようとしている本です。
abc予想とは何でしょうか?
abcという名前は、
\[ \begin{aligned}a+b=c\end{aligned} \]
という式に由来します。単純。\(a,b,c\)は自然数。つまり、数に関する予想です。数の性質の研究は、大学数学においては数論(number theory)と呼ばれる分野に分類されます。フェルマー予想も、リーマン予想も、数の性質に関する予想、数論の予想です。
特にabc予想に近くて有名なのが、フェルマー予想です。それは
\[ \begin{aligned}x^n +y ^n =z ^n \end{aligned} \]
を満たす自然数\(x,y,z\)は、\(n\geq 3 \)のとき存在しない、という主張。abc予想流に言えば、これはxyz予想というネーミングになったでしょう。
\(3^2 +4^2 =5^2\)のように、\(n=2\)ならいくらでも見つけることができます(ピタゴラス数)。しかし\(n \geq 3\)となるとぱたりと見つからなくなるのですから、不思議です。
この予想は数学者のフェルマーによって1637年頃に提示されました。そして「この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる。 」という有名な言葉を残しています。その後多くの数学者がこの問題に挑戦しましたが、それはずっと解かれないままでした。おそらくフェルマーが解けたと思っていた方法は、何らかの間違いがあったのでしょう。
そして1995年に、アンドリュー・ワイルズによって正しいと証明されました。提示から約360年後、それだけ難問だったものが解けたのですから驚きです。数学の問題、特に難しい問題=予想は、それが発見されてから、解決に至るまでにものすごい時間がかかるのが普通です。
ワイルズが示したのは、フェルマーの予想だけでなく、それを含む大きな予想、志村-谷村予想でした。その問題に注目するだけでなく、問題を大きく抽象化し、特には新しい枠組みを生み出し、知見を積み重ねていかなければ、予想は解けないものなんですね。
abc予想は、1985年にジョゼフ・オステルレとデイヴィッド・マッサーにより提示されました。そして、2012年に、日本の数学者・望月新一がそれを解決したとする論文を、自身のホームページに発表しました。
それは宇宙際(うちゅうさい)タイヒミューラー理論(Inter-universal Teichmuller Theory、IUT理論)という理論で、それによってabc予想が示されるというもの。日本語で解説文「宇宙際タイヒミューラー理論への誘(いざな)い」がありますが、専門用語から始まって、日本語でもとても読めないでしょう。
学術論文は、数学者によってチェック=査読され、学会雑誌に載せられること(パブリッシュ)で信頼されますが、その作業には時間がかかっています。新しい理論・用語が多く難解であることもあり、数論を専門とする数学者の間でもまだ見解は一致していないようです。
2020年には京都大学数理解析研究所(RIMS)の雑誌に掲載されることになり、証明されたと報じられています。しかし、同じく数論の専門家であるピーター・ショルツはその証明に納得していません。
参考:未解明だった数学の超難問「ABC予想」を証明 京大の望月教授 斬新・難解で査読に8年 – 朝日新聞、ABC予想「証明は本当か?」 欧米で論文に異議相次ぐ、
で、abc予想って何なのって話なんですが……。
任意の\(\epsilon >0\)に対して、次の条件を満たすある正の定数\(K>0\)が存在する。
\(a,b,c\)を互いに素な整数で、\(a+b=c\)を満たすものとするならば、
\[ \begin{aligned}\max\{|a|,|b|,|c|\}< K (\mathrm{rad}(abc)) ^{1+\epsilon}\end{aligned} \]
が成立。
難しくなってしまいました。次の強いabc予想と呼ばれる形式は少し簡単になります。
\(a,b,c\)を互いに素な整数で、\(a+b=c\)を満たすものとするならば、
\[ \begin{aligned}\max\{|a|,|b|,|c|\}< (\mathrm{rad}(abc)) ^{2}\end{aligned} \]
が成立。
例えば、\(a=1,b=8,c=9\)としてみましょう。これは\(a+b=c\)を満たします。
互いに素な数というのは、共通の約数のうち最大のもの=最大公約数1である数たちのこと。\(1,8,9\)の最大公約数は1なので、互いに素です。
\(\max\{|a|,|b|,|c|\}\)は、\(a,b,c\)の(絶対値)の最大値のこと。ここでは、\(c\)が最大なので、\(\max\{|a|,|b|,|c|\}=9\)。
\(\mathrm{rad}\)は馴染みのないものかもしれません。これは整数の根基(radical)と呼ばれる量です。\(\mathrm{rad}(n)\)で、\(n\)の素因数の積を表します。\(abc=72\)では、\(72=2^3 \cdot 3^2\)と素因数分解されるので、その素因数部分\(2,3\)をかけあわせて、\(\mathrm{rad}(abc)=6\)となります。
つまり、\(a=1,b=8,c=9\)のとき、\(\max\{|a|,|b|,|c|\}=9<36 =(\mathrm{rad}(abc)) ^{2}\)と、強いABC予想は成り立っています。
一方で、この不等式の右辺のべき乗を1にしてしまうと、\(\max\{|a|,|b|,|c|\}=9 \not <6 =\mathrm{rad}(abc)\)となり成立しません。
つまり、元のabc予想において、\(\varepsilon =0, K=1\)バージョンは成立しません。そこでそれを少し弱めて、\(1+\varepsilon\)乗に対して、適切に\(K\)を決めることができて、
\[ \begin{aligned}\max\{|a|,|b|,|c|\}< K (\mathrm{rad}(abc)) ^{1+\epsilon}\end{aligned} \]
ならば成立しているんじゃないか、というのがabc予想です。
\(a+b=c\)という和と、その積の素数成分の大きさ(根基 \(\mathrm{rad}(abc)\))に関するもの、くらいの説明で、わかりやすくなったでしょうか。
本の目次
ABC予想入門の目次を紹介します。
- 数学の予想とは
- 素数と絶対数学入門
- abc予想の歴史
- 多項式abc予想の証明
- 楕円曲線と保型形式の古典理論
- 整数abc予想の証明へ:絶対数学
「3.2 abc予想とは」において、abc予想の主張(ステートメント)が書かれています。
つまり、そこより前はあまり数学そのものの知識がなくても読めます。特に1章は、abc予想に限らず、「数学の予想とはどういうものなのか?どうやって解決に向かうのか?」が解説されていて、面白いです。問題を類似のものに変形したり、分割したりすることで、予想といっても様々な形を取ることがわかります。
4章以降は、大学数学の代数学の知識がないと読むのが難しく感じるでしょう。下の図で言えば、まず代数学基礎(群・環・体)をベースにした用語は必要です。
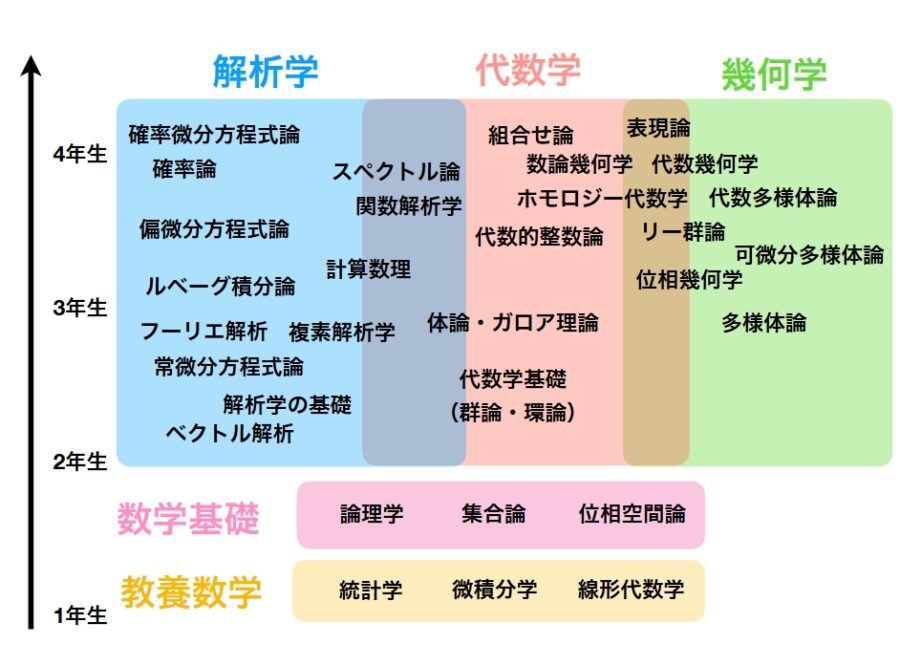
さらに、数論幾何、特に楕円曲線論に関する話が登場します。楕円曲線という名前ですが、ラグビーボールのような形の曲線(2次曲線)ではなく、整数との関係をもつ特殊な平面曲線(3次曲線)です。楕円曲線のようすを分析するために、多様体論の考え方も必要になります。
偉大な数学者のガウスは「数学は科学の女王であり、数論は数学の女王である」といった言葉を残したそうですが、まさにその通りで、数論はその見かけのシンプルさ(?)によらず、幅広い分野の数学の知識が要求されます。でもその奥深さ込みで、登るべき山があるという面白さにもなりますね。
気になる点
1~3章は一般書のレベルですが、4章以降は(仕方のないことかもしれませんが)専門書のレベルで難しいです。コンパクトに説明する都合上、説明の文面が足りず、論文へのガイドとして使うことになるでしょう。
数論に関する大学数学を学ぶならば、まず大数学基礎、群論から触れてみるのはいかがでしょうか。
参考:群論入門~回転群と巡回群を例に、群の定義・同型・位数を解説、群論からガロア理論への入門(五次方程式の解の公式は存在しない)
また、abc予想の証明を与えているとされる望月論文、IUT理論についての解説は数ページ。その内容はほぼわかりません。知りたければ別の本、例えば「宇宙と宇宙をつなぐ数学 IUT理論の衝撃」を読む必要があるでしょう。
数の話の随所に「絶対数学」という著者の用語がたびたび登場するのですが、これがabc予想や素数の解説にそれほど関係するのかよくわかりませんでした。別の著書の宣伝の面があるのでしょうか。ほかの歴史や数学に関する記述は、全体的に出典・根拠が示され、きちんとしていると思います。
僕は「ABC予想入門」を、Kindleの読み放題サービスKindle Unlimitedで読みました。登録してあれば無料なので、ぜひ試しに読んでみてください。数に関するホットな予想:abc予想に触れつつ、数学の予想とはどういうものか知ることができるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
PHP研究所 (2013-07-19T00:00:00.000Z)
¥765
宇宙と宇宙をつなぐ数学 IUT理論の衝撃 (角川学芸出版単行本)
KADOKAWA (2019-04-25T00:00:00.000Z)
¥1,584
日本評論社 (2013-10-15T00:00:01Z)
¥3,740
日経BP (2004-08-30T00:00:00.000Z)
¥2,860
新潮社 (2006-06-01T00:00:00.000Z)
¥782
こちらもおすすめ
群論からガロア理論への入門(五次方程式の解の公式は存在しない)
リーマン予想を眺めてみよう 「素数に憑かれた人たち」レビュー






